Prosta regresja liniowa

W tym artykule wyjaśniono, czym jest prosta regresja liniowa w statystyce i jak jest wykonywana. W Internecie znajdziesz także rozwiązanie prostego ćwiczenia regresji liniowej oraz dodatkowo prosty kalkulator regresji liniowej.

Co to jest prosta regresja liniowa?

Prosta regresja liniowa to model statystyczny używany do powiązania zmiennej niezależnej i staramy się przybliżyć związek Co istnieje pomiędzy dwiema zmiennymi.

Dlatego do znalezienia równania, które łączy liniowo dwie zmienne, stosuje się prostą regresję liniową. Logicznie rzecz biorąc, związek między dwiema zmiennymi musi być liniowy, w przeciwnym razie należy zastosować inny typ modelu regresji.

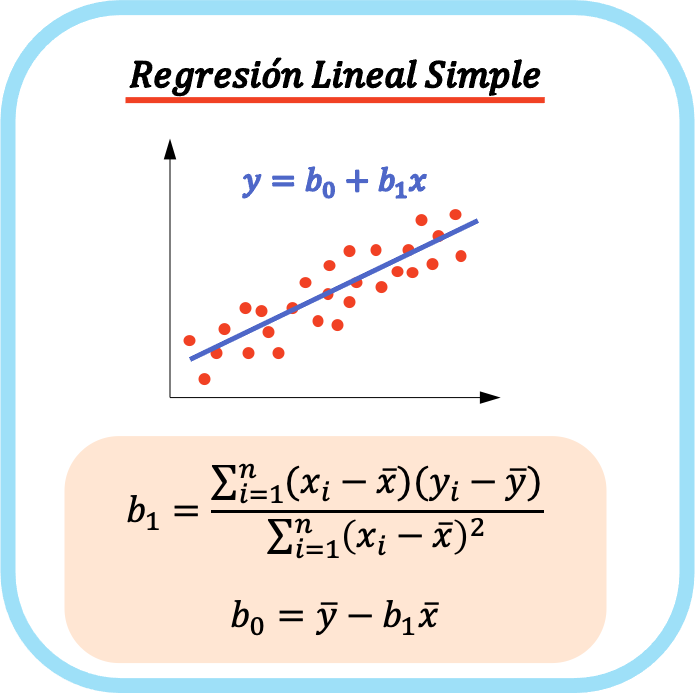
Równanie prostego modelu regresji liniowej składa się z dwóch współczynników: stałej równania (b ₀ ) i współczynnika korelacji pomiędzy obiema zmiennymi (b ₁ ). Dlatego równanie prostego modelu regresji liniowej to y=b ₀ +b ₁ x.

Równanie prostej regresji liniowej przedstawiono na wykresie jako linię prostą, więc współczynnik b ₀ to punkt przecięcia, a współczynnik b ₁ to nachylenie linii.

Proste wzory regresji liniowej

Wzory na obliczenie współczynników prostej regresji liniowej są następujące:

👉 Poniższy kalkulator umożliwia obliczenie współczynników prostej regresji liniowej dla dowolnego zbioru danych.

Oczywiście równanie wynikające z prostego modelu regresji liniowej nie będzie w stanie odgadnąć dokładnej wartości wszystkich obserwacji, ponieważ model ten po prostu próbuje znaleźć równanie przybliżające zależność między dwiema zmiennymi. Zatem resztę definiuje się jako różnicę między wartością prawdziwą a wartością oszacowaną za pomocą modelu regresji liniowej.

Należy zauważyć, że celem prostego modelu regresji liniowej jest minimalizacja kwadratów reszt, co oznacza, że prosta regresja liniowa opiera się na kryterium najmniejszych kwadratów .

Konkretny przykład prostej regresji liniowej

Aby zakończyć zrozumienie metody prostej regresji liniowej, poniżej znajduje się praktyczny przykład krok po kroku, w którym równanie prostego modelu regresji liniowej jest obliczane na podstawie zestawu danych statystycznych.

• Po zdaniu egzaminu ze statystyki pięciu studentów zostało zapytanych, ile godzin nauki poświęcili na egzamin. Dane zostały zaprezentowane w poniższej tabeli. Wykonaj prosty model regresji liniowej zebranych danych statystycznych, aby liniowo powiązać godziny nauki z uzyskaną oceną.

Aby przeprowadzić prosty model regresji liniowej, musimy wyznaczyć współczynniki b ₀ i b ₁ równania i w tym celu musimy skorzystać ze wzorów przedstawionych w powyższej sekcji.

Aby jednak zastosować proste wzory regresji liniowej, musimy najpierw obliczyć średnią zmiennej niezależnej i średnią zmiennej zależnej:

Teraz, gdy znamy średnie zmiennych, obliczamy współczynnik b ₁ modelu, korzystając z odpowiedniego wzoru:

Na koniec obliczamy współczynnik b ₀ modelu, korzystając z odpowiedniego wzoru:

Krótko mówiąc, równanie prostego modelu regresji liniowej problemu wygląda następująco:

Poniżej możesz zobaczyć graficzną reprezentację przykładowych danych, a także linię prostą prostego modelu regresji liniowej:

Na koniec, gdy już obliczyliśmy równanie prostego modelu regresji liniowej, pozostaje nam jedynie zinterpretować uzyskany wynik. W tym celu niezbędne jest obliczenie współczynnika determinacji modelu regresji, można zobaczyć jak to się robi wyszukując odpowiedni artykuł na naszej stronie internetowej.

Proste założenia regresji liniowej

Aby przeprowadzić prostą regresję liniową należy spełnić następujące założenia:

• Niezależność : obserwowane reszty muszą być od siebie niezależne. Powszechnym sposobem zapewnienia niezależności modelu jest dodanie losowości do procesu próbkowania.
• Homoscedastyczność : wariancje reszt muszą być jednorodne, to znaczy zmienność reszt musi być stała.
• Normalność : reszty muszą mieć rozkład normalny, czyli innymi słowy muszą mieć rozkład normalny ze średnią 0.
• Liniowość – zależność pomiędzy zmienną niezależną a zmienną zależną powinna być liniowa.

Prosty kalkulator regresji liniowej

Podłącz przykładowe dane do poniższego kalkulatora, aby dopasować prosty model regresji liniowej pomiędzy dwiema zmiennymi. Należy rozdzielić pary danych tak, aby w pierwszym polu znajdowały się tylko wartości zmiennej niezależnej X, a w drugim polu znajdowały się wyłącznie wartości zmiennej zależnej Y.

Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.

Prosta i wielokrotna regresja liniowa

Na koniec zobaczymy, jaka jest różnica między prostą regresją liniową a wielokrotną regresją liniową, ponieważ są to dwa rodzaje regresji liniowej często stosowane w statystyce.

Wielokrotna regresja liniowa umożliwia matematyczne powiązanie dwóch lub większej liczby zmiennych objaśniających ze zmienną odpowiedzi. Oznacza to, że w wielokrotnej regresji liniowej tworzony jest model, w którym występują co najmniej dwie zmienne niezależne.

Dlatego różnica między prostą regresją liniową a wielokrotną regresją liniową polega na liczbie zmiennych niezależnych. W prostej regresji liniowej istnieje tylko jedna zmienna niezależna, podczas gdy w wielokrotnej regresji liniowej istnieją dwie lub więcej zmiennych niezależnych.