Jak wykonać prostą regresję liniową w r (krok po kroku)
Prosta regresja liniowa to technika, której możemy użyć do zrozumienia związku pomiędzy pojedynczą zmienną objaśniającą a pojedynczą zmienną odpowiedzi .
W skrócie, technika ta znajduje linię, która najlepiej „pasuje” do danych i przyjmuje następującą formę:
ŷ = b 0 + b 1 x
Złoto:
- ŷ : Szacowana wartość odpowiedzi
- b 0 : Początek linii regresji
- b 1 : Nachylenie linii regresji
Równanie to może pomóc nam zrozumieć związek pomiędzy zmienną objaśniającą a zmienną odpowiedzi oraz (zakładając, że jest istotne statystycznie) może zostać wykorzystane do przewidywania wartości zmiennej odpowiedzi, biorąc pod uwagę wartość zmiennej objaśniającej.
W tym samouczku wyjaśniono krok po kroku, jak przeprowadzić prostą regresję liniową w języku R.
Krok 1: Załaduj dane
Na potrzeby tego przykładu utworzymy fałszywy zbiór danych zawierający dwie zmienne dla 15 uczniów:
- Łączna liczba godzin poświęconych na niektóre egzaminy
- Wynik egazminu
Spróbujemy dopasować prosty model regresji liniowej, wykorzystując godziny jako zmienną objaśniającą i wyniki badań jako zmienną odpowiedzi.
Poniższy kod pokazuje, jak utworzyć ten fałszywy zbiór danych w R:
#create dataset df <- data.frame(hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14), score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89)) #view first six rows of dataset head(df) hours score 1 1 64 2 2 66 3 4 76 4 5 73 5 5 74 6 6 81 #attach dataset to make it more convenient to work with attach(df)
Krok 2: Wizualizuj dane
Przed dopasowaniem prostego modelu regresji liniowej musimy najpierw wizualizować dane, aby je zrozumieć.
Po pierwsze, chcemy się upewnić, że związek między godzinami a wynikiem jest w przybliżeniu liniowy, ponieważ jest to ogromne założenie leżące u podstaw prostej regresji liniowej. Możemy utworzyć prosty wykres rozrzutu, aby zwizualizować związek między dwiema zmiennymi:
scatter.smooth(hours, score, main=' Hours studied vs. Exam Score ')
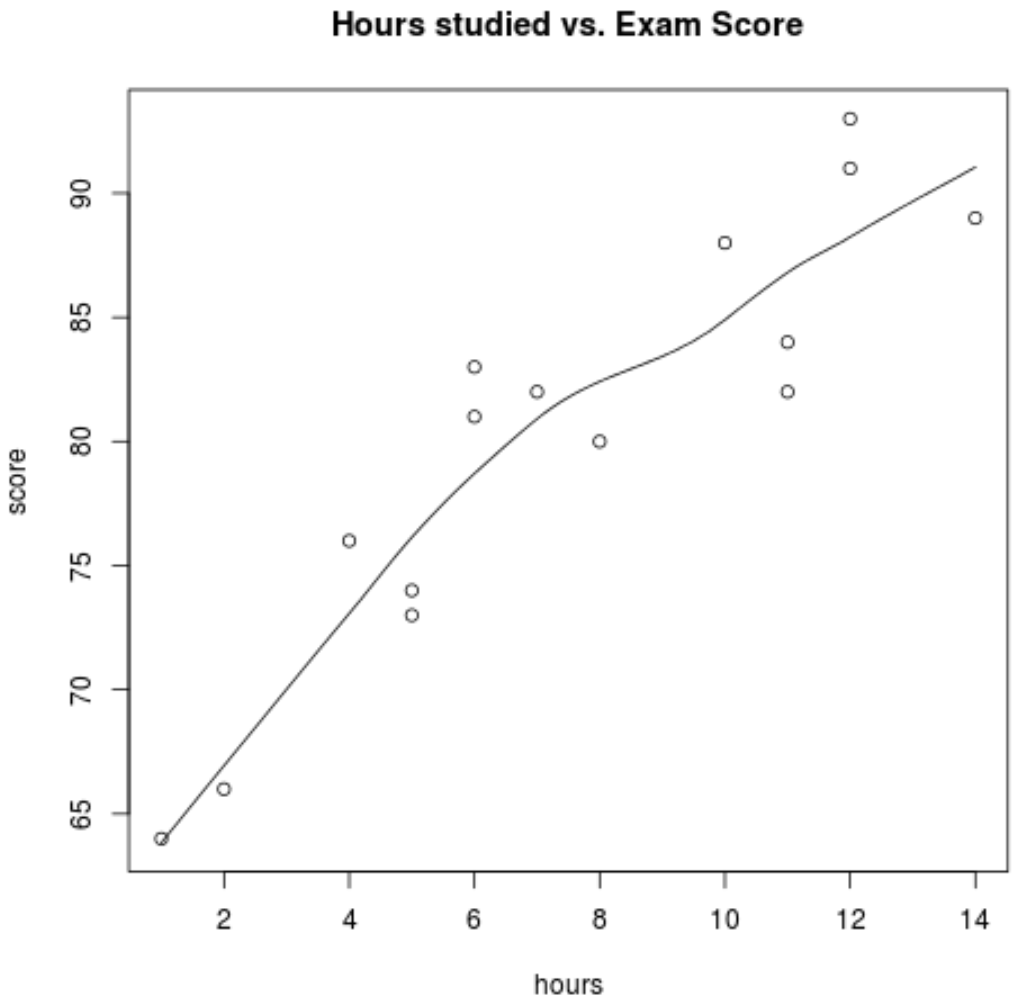
Z wykresu widać, że zależność wydaje się być liniowa. Wraz ze wzrostem liczby godzin wynik również ma tendencję do zwiększania się liniowo.
Następnie możemy utworzyć wykres pudełkowy, aby zwizualizować rozkład wyników egzaminu i sprawdzić wartości odstające . Domyślnie R definiuje obserwację jako wartość odstającą, jeśli jest 1,5-krotnością rozstępu międzykwartylowego powyżej trzeciego kwartyla (Q3) lub 1,5-krotności rozstępu międzykwartylowego poniżej pierwszego kwartyla (Q1).
Jeśli obserwacja jest odstająca, na wykresie pudełkowym pojawi się małe kółko:
boxplot(score)
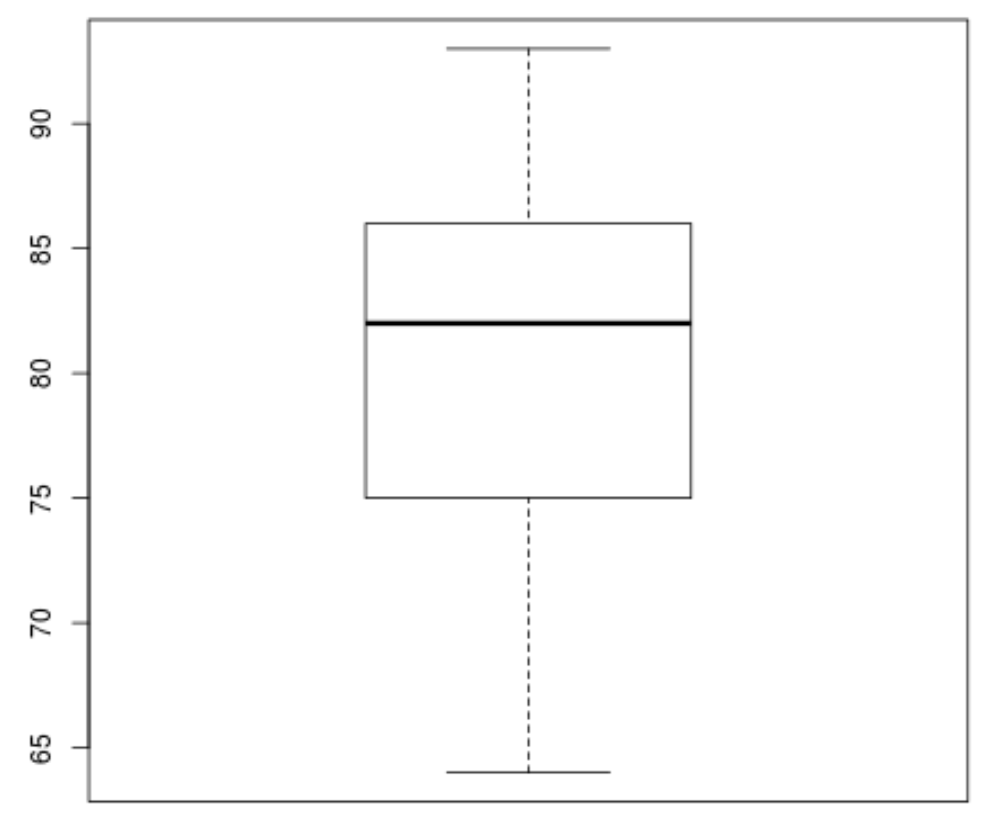
Na wykresie pudełkowym nie ma małych okręgów, co oznacza, że w naszym zbiorze danych nie ma wartości odstających.
Krok 3: Wykonaj prostą regresję liniową
Kiedy już potwierdzimy, że związek między naszymi zmiennymi jest liniowy i nie ma żadnych wartości odstających, możemy przystąpić do dopasowania prostego modelu regresji liniowej, wykorzystując godziny jako zmienną objaśniającą i wynik jako zmienną odpowiedzi:
#fit simple linear regression model model <- lm(score~hours) #view model summary summary(model) Call: lm(formula = score ~ hours) Residuals: Min 1Q Median 3Q Max -5,140 -3,219 -1,193 2,816 5,772 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 65,334 2,106 31,023 1.41e-13 *** hours 1.982 0.248 7.995 2.25e-06 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 3.641 on 13 degrees of freedom Multiple R-squared: 0.831, Adjusted R-squared: 0.818 F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06
Z podsumowania modelu widzimy, że dopasowane równanie regresji ma postać:
Wynik = 65,334 + 1,982*(godziny)
Oznacza to, że każda dodatkowa godzina nauki wiąże się ze średnim wzrostem wyniku z egzaminu o 1982 punkty. Oryginalna wartość 65 334 mówi nam, jaki jest średni oczekiwany wynik egzaminu dla studenta studiującego przez zero godzin.
Możemy również użyć tego równania, aby znaleźć oczekiwany wynik egzaminu na podstawie liczby godzin spędzonych przez studenta. Przykładowo student studiujący 10 godzin powinien uzyskać z egzaminu wynik 85,15 :
Wynik = 65,334 + 1,982*(10) = 85,15
Oto jak zinterpretować pozostałą część podsumowania modelu:
- Pr(>|t|): Jest to wartość p powiązana ze współczynnikami modelu. Ponieważ wartość p dla godzin (2,25e-06) jest znacznie mniejsza niż 0,05, możemy powiedzieć, że istnieje statystycznie istotny związek między godzinami a wynikiem .
- Wielokrotne R-kwadrat: Liczba ta mówi nam, że procent zróżnicowania wyników egzaminu można wyjaśnić liczbą godzin nauki. Ogólnie rzecz biorąc, im większa wartość R-kwadrat modelu regresji, tym lepiej zmienne objaśniające są w stanie przewidzieć wartość zmiennej odpowiedzi. W tym przypadku 83,1% różnic w wynikach można wyjaśnić liczbą przepracowanych godzin.
- Resztkowy błąd standardowy: jest to średnia odległość pomiędzy obserwowanymi wartościami a linią regresji. Im niższa jest ta wartość, tym bardziej linia regresji może odpowiadać obserwowanym danym. W tym przypadku średni wynik zaobserwowany na egzaminie odbiega o 3641 punktów od wyniku przewidywanego przez linię regresji.
- Statystyka F i wartość p: Statystyka F ( 63,91 ) i odpowiadająca jej wartość p ( 2.253e-06 ) mówią nam o ogólnym znaczeniu modelu regresji, tj. czy zmienne objaśniające w modelu są przydatne do wyjaśnienia zmienności . w zmiennej odpowiedzi. Ponieważ wartość p w tym przykładzie jest mniejsza niż 0,05, nasz model jest istotny statystycznie i godziny uważa się za przydatne do wyjaśnienia zmienności wyniku .
Krok 4: Utwórz działki resztkowe
Po dopasowaniu prostego modelu regresji liniowej do danych ostatnim krokiem jest utworzenie wykresów reszt.
Jednym z kluczowych założeń regresji liniowej jest to, że reszty modelu regresji mają w przybliżeniu rozkład normalny i są homoskedastyczne na każdym poziomie zmiennej objaśniającej. Jeżeli te założenia nie zostaną spełnione, wyniki naszego modelu regresji mogą wprowadzać w błąd lub być niewiarygodne.
Aby sprawdzić, czy założenia te są spełnione, możemy utworzyć następujące wykresy reszt:
Wykres reszt w funkcji dopasowanych wartości: Wykres ten jest przydatny do potwierdzenia homoskedastyczności. Oś x wyświetla dopasowane wartości, a oś y wyświetla reszty. Dopóki reszty wydają się być losowo i równomiernie rozmieszczone na wykresie wokół wartości zerowej, możemy założyć, że homoskedastyczność nie jest naruszona:
#define residuals res <- resid(model) #produce residual vs. fitted plot plot(fitted(model), res) #add a horizontal line at 0 abline(0,0)
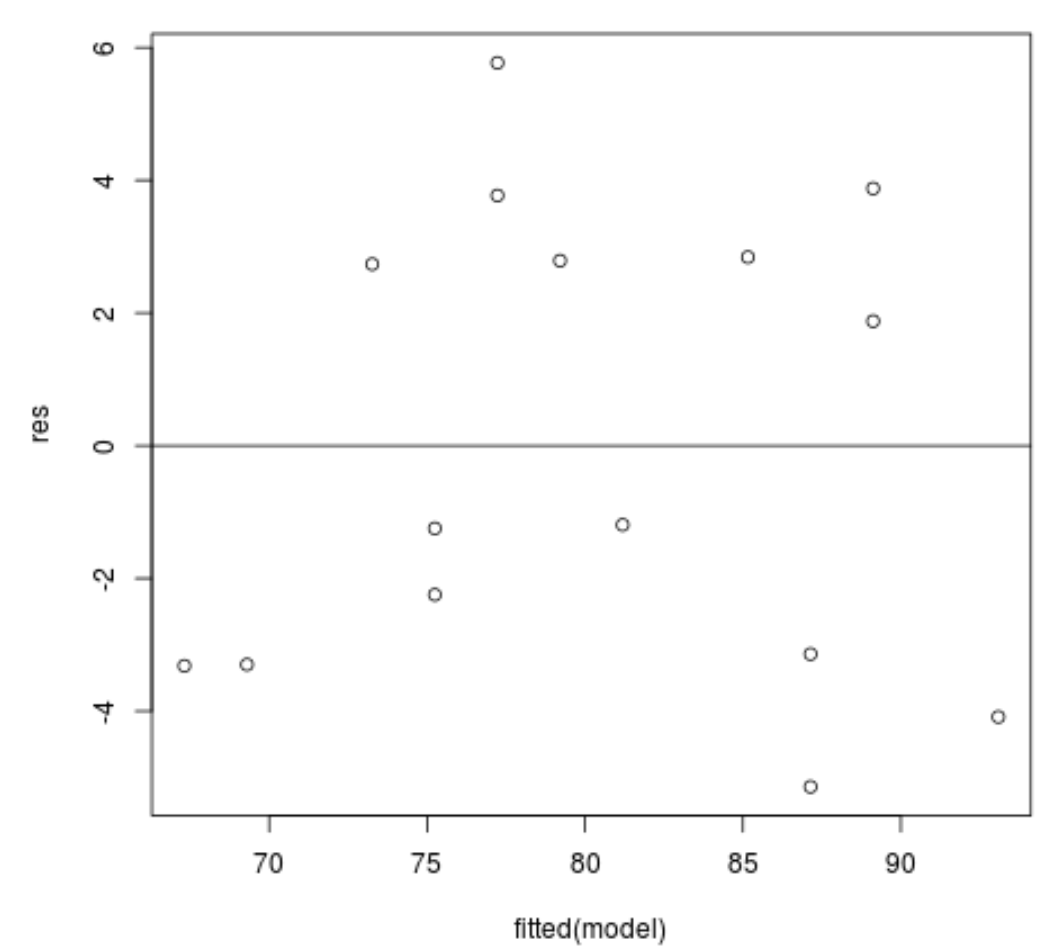
Reszty wydają się być losowo rozproszone wokół zera i nie wykazują zauważalnego wzoru, więc to założenie jest spełnione.
Wykres QQ: Ten wykres jest przydatny do określenia, czy reszty mają rozkład normalny. Jeśli wartości danych na wykresie przebiegają mniej więcej po linii prostej pod kątem 45 stopni, wówczas dane mają rozkład normalny:
#create QQ plot for residuals qqnorm(res) #add a straight diagonal line to the plot qqline(res)
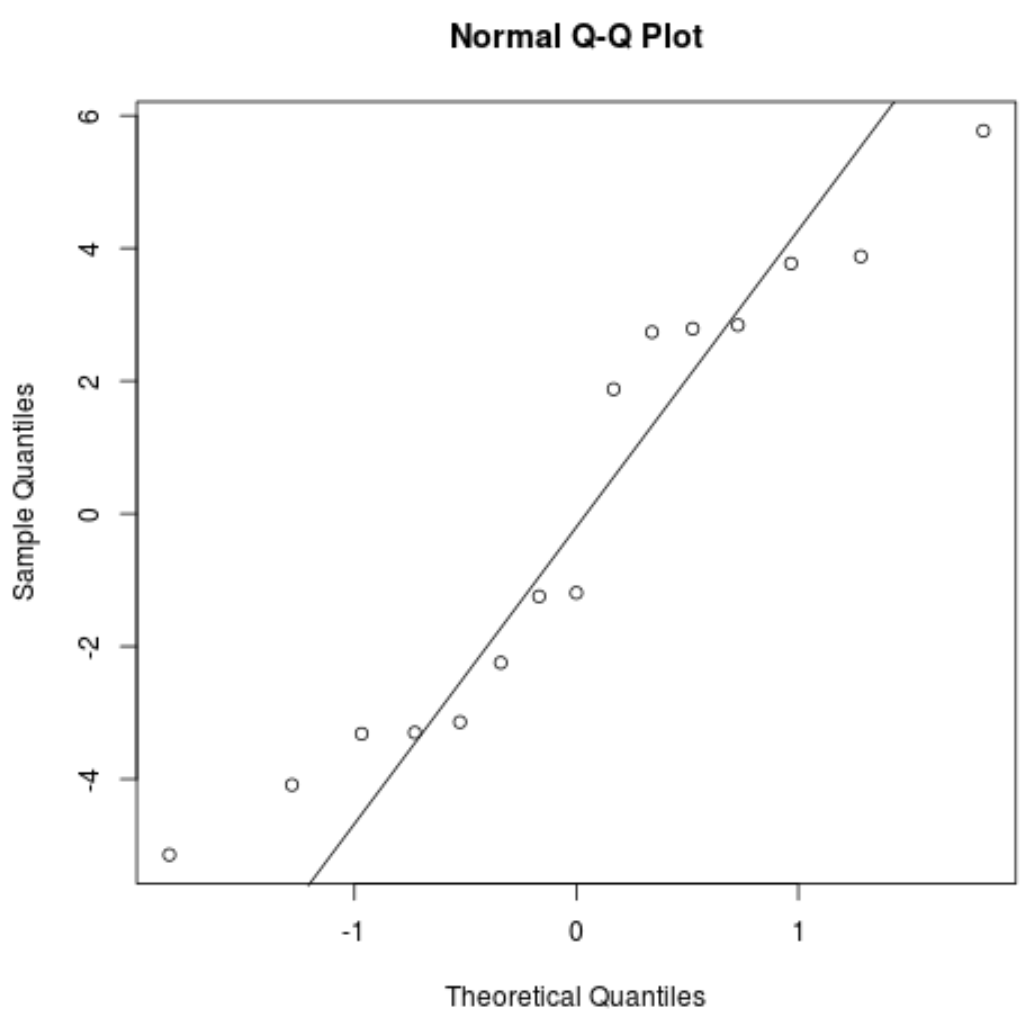
Wartości resztkowe odbiegają nieco od linii 45 stopni, ale nie na tyle, aby powodować poważne obawy. Można założyć, że założenie normalności jest spełnione.
Ponieważ reszty mają rozkład normalny i homoskedastyczny, sprawdziliśmy, czy spełnione są założenia prostego modelu regresji liniowej. Zatem wynik naszego modelu jest niezawodny.
Pełny kod R użyty w tym samouczku można znaleźć tutaj .