Jak wykonać prostą regresję liniową w sas-ie

Prosta regresja liniowa to technika, którą możemy wykorzystać do zrozumienia związku między zmienną predykcyjną a zmienną odpowiedzi .

Technika ta znajduje linię, która najlepiej „pasuje” do danych i przyjmuje następującą postać:

ŷ = b ₀ + b ₁ x

Złoto:

• ŷ : Szacowana wartość odpowiedzi
• b ₀ : Początek linii regresji
• b ₁ : Nachylenie linii regresji

To równanie pomaga nam zrozumieć związek między zmienną predykcyjną a zmienną odpowiedzi.

Poniższy przykład pokazuje krok po kroku jak przeprowadzić prostą regresję liniową w SAS-ie.

Krok 1: Utwórz dane

Na potrzeby tego przykładu utworzymy zbiór danych zawierający całkowitą liczbę przepracowanych godzin i oceny z egzaminu końcowego 15 uczniów.

Dopasujemy prosty model regresji liniowej, wykorzystując godziny jako zmienną predykcyjną i wynik jako zmienną odpowiedzi.

Poniższy kod pokazuje, jak utworzyć ten zbiór danych w SAS-ie:

 /*create dataset*/
data exam_data;
    input hours score;
    datalines ;
1 64
2 66
4 76
5 73
5 74
6 81
6 83
7 82
8 80
10 88
11 84
11 82
12 91
12 93
14 89
;
run ;

/*view dataset*/
proc print data =exam_data;

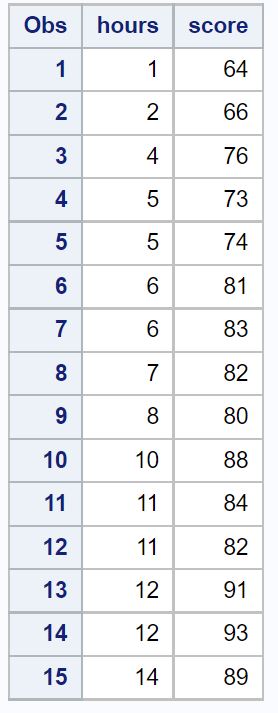
Krok 2: Dopasuj prosty model regresji liniowej

Następnie użyjemy proc reg , aby dopasować prosty model regresji liniowej:

 /*fit simple linear regression model*/
proc reg data =exam_data;
   model score = hours;
run ; 

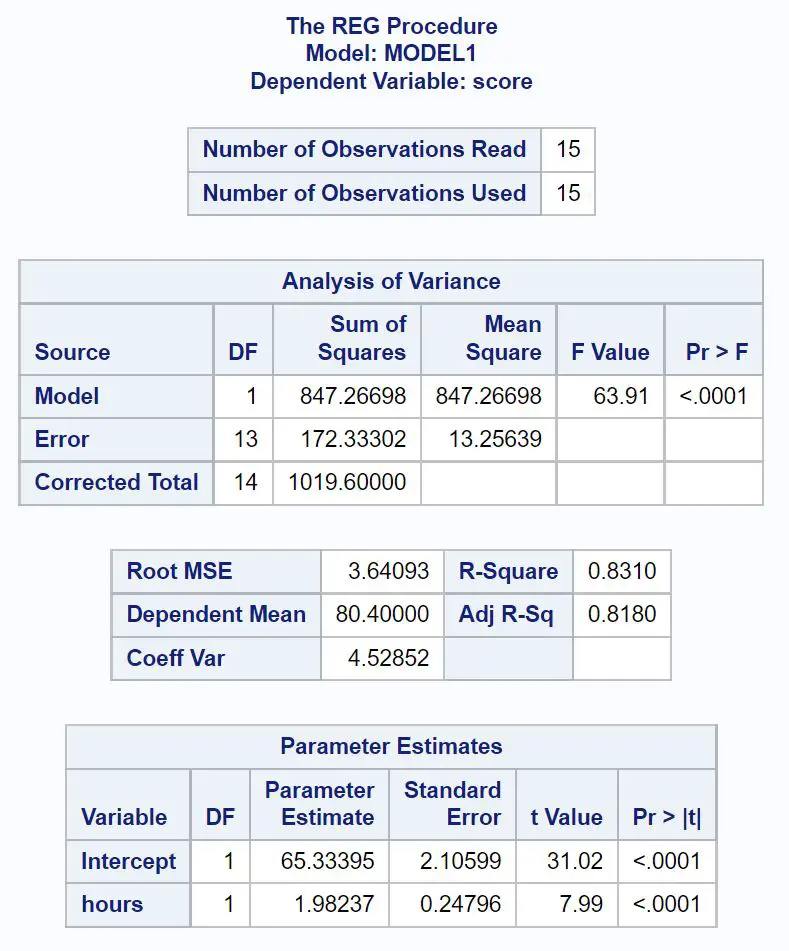
Oto jak zinterpretować w wyniku najważniejsze wartości z każdej tabeli:

Tabela analizy luk:

Ogólna wartość F modelu regresji wynosi 63,91 , a odpowiadająca jej wartość p wynosi <0,0001 .

Ponieważ ta wartość p jest mniejsza niż 0,05, dochodzimy do wniosku, że model regresji jako całość jest istotny statystycznie. Innymi słowy, godziny są użyteczną zmienną do przewidywania wyników egzaminu.

Tabela dopasowania modelu:

Wartość R-Square informuje nas o procentowym zróżnicowaniu wyników egzaminu, które można wytłumaczyć liczbą godzin nauki.

Ogólnie rzecz biorąc, im większa wartość R-kwadrat modelu regresji, tym lepiej zmienne predykcyjne przewidują wartość zmiennej odpowiedzi.

W tym przypadku 83,1% różnic w wynikach egzaminów można wytłumaczyć liczbą godzin nauki. Wartość ta jest dość wysoka, co wskazuje, że przepracowane godziny są bardzo przydatną zmienną w przewidywaniu wyników egzaminu.

Tabela oszacowań parametrów:

Z tej tabeli możemy zobaczyć dopasowane równanie regresji:

Wynik = 65,33 + 1,98*(godziny)

Interpretujemy to w ten sposób, że każda dodatkowa godzina nauki wiąże się ze średnim wzrostem wyniku egzaminu o 1,98 punktu .

Oryginalna wartość mówi nam, że średni wynik egzaminu dla studenta studiującego zero godzin wynosi 65,33 .

Możemy również użyć tego równania, aby znaleźć oczekiwany wynik egzaminu na podstawie liczby godzin spędzonych przez studenta.

Przykładowo student studiujący 10 godzin powinien uzyskać z egzaminu wynik 85,13 :

Wynik = 65,33 + 1,98*(10) = 85,13

Ponieważ wartość p (<0,0001) dla godzin jest w tej tabeli mniejsza niż 0,05, dochodzimy do wniosku, że jest to statystycznie istotna zmienna predykcyjna.

Krok 3: Przeanalizuj wykresy reszt

Prosta regresja liniowa przyjmuje dwa ważne założenia dotyczące reszt modelu:

• Reszty mają rozkład normalny.
• Reszty mają równą wariancję („ homoscedastyczność ”) na każdym poziomie zmiennej predykcyjnej.

Jeżeli te założenia nie zostaną spełnione, wyniki naszego modelu regresji mogą nie być wiarygodne.

Aby sprawdzić, czy te założenia są spełnione, możemy przeanalizować wykresy reszt, które SAS automatycznie wyświetla w wynikach:

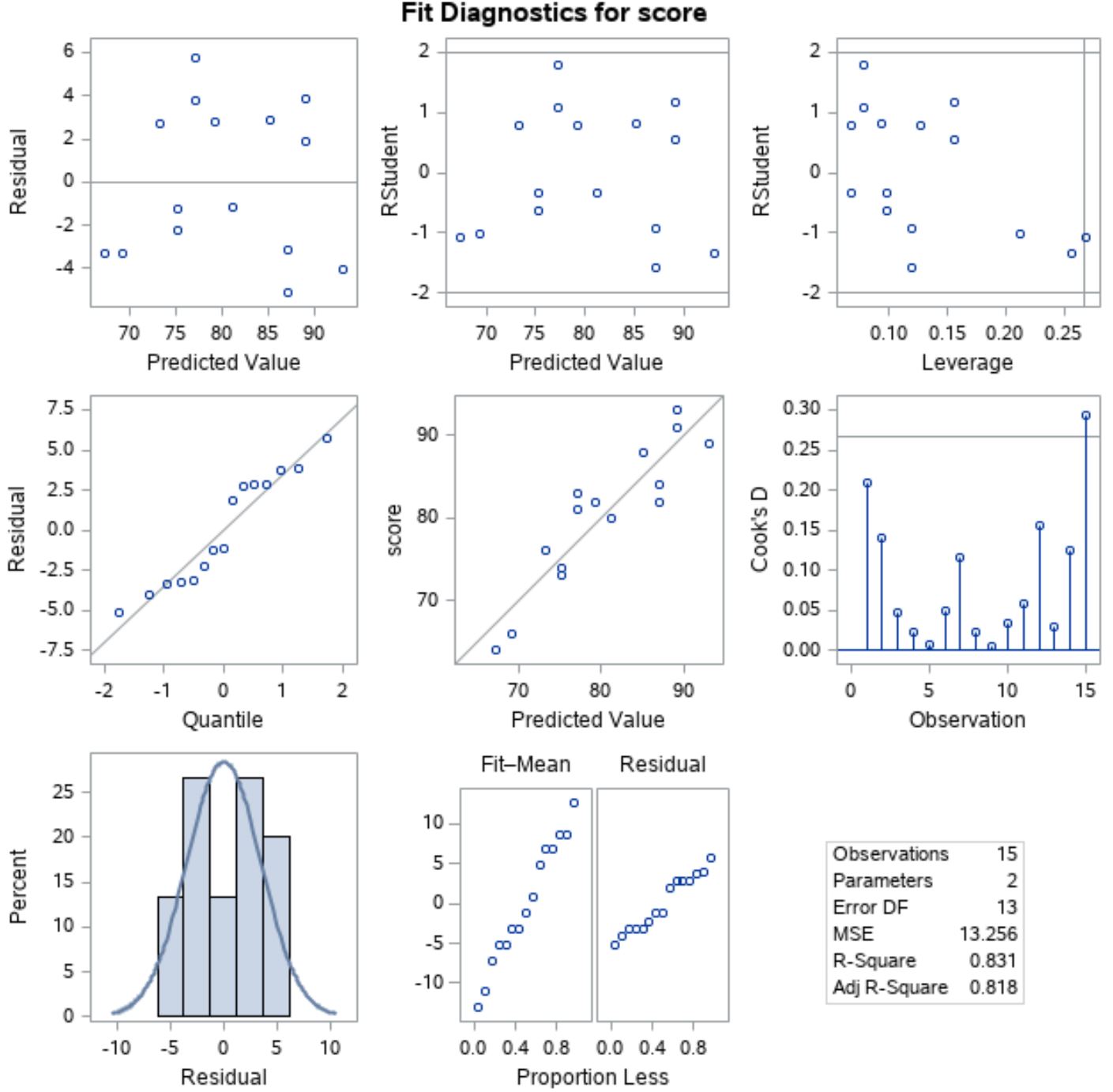
Aby sprawdzić, czy reszty mają rozkład normalny , możemy przeanalizować wykres po lewej stronie środkowej linii z „kwantylem” na osi x i „resztą” na osi y.

Wykres ten nazywany jest wykresem QQ , w skrócie „kwantyl-kwantyl”, i służy do określenia, czy dane mają rozkład normalny, czy nie. Jeśli dane mają rozkład normalny, punkty na wykresie QQ będą leżeć na prostej ukośnej.

Z wykresu widać, że punkty leżą mniej więcej na prostej ukośnej, zatem możemy założyć, że reszty mają rozkład normalny.

Następnie, aby sprawdzić, czy reszty są homoskedastyczne , możemy spojrzeć na wykres po lewej stronie pierwszego wiersza z wartością „przewidywaną” na osi x i wartością „resztową” na osi y.

Jeśli punkty wykresu są losowo rozproszone wokół zera i nie ma wyraźnego wzoru, wówczas możemy założyć, że reszty są homoskedastyczne.

Z wykresu widać, że punkty są losowo rozproszone wokół zera z w przybliżeniu równą wariancją na każdym poziomie na całym wykresie, zatem możemy założyć, że reszty są homoskedastyczne.

Ponieważ oba założenia są spełnione, możemy założyć, że wyniki prostego modelu regresji liniowej są wiarygodne.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w SAS-ie:

Jak wykonać jednokierunkową ANOVA w SAS
Jak wykonać dwukierunkową ANOVA w SAS
Jak obliczyć korelację w SAS-ie