Proste losowe pobieranie próbek
W tym artykule dowiesz się, czym jest prosta próbka losowa i jakie istnieją rodzaje prostych próbek losowych. Dodatkowo na przykładzie wyjaśniamy, jak przeprowadzane jest proste losowe pobieranie próbek. Wreszcie będziesz mógł zobaczyć, jakie są zalety i wady prostego losowego pobierania próbek.
Co to jest proste próbkowanie losowe?
W statystyce dobór losowy prosty jest metodą probabilistyczną stosowaną do doboru próby do badania. Główną cechą prostego doboru losowego jest to, że daje każdemu elementowi populacji statystycznej takie samo prawdopodobieństwo znalezienia się w badanej próbie.
W przypadku prostego próbkowania losowego elementy próbki dobierane są losowo, zatem otrzymana próbka jest całkowicie losowa.
Zatem stosując dobór losowy prosty, prawdopodobieństwo otrzymania danej próbki jest równe prawdopodobieństwu otrzymania dowolnej innej próbki. Zobaczymy poniżej, jak obliczane jest to prawdopodobieństwo.
Należy pamiętać, że istnieją inne sposoby selekcji osób z próby. Najczęściej stosowane rodzaje pobierania próbek to głównie:
- Proste losowe pobieranie próbek
- Próbkowanie warstwowe
- Systematyczne pobieranie próbek
- Próbkowanie klastrów
Koncepcja prostego próbkowania losowego jest z pewnością najłatwiejsza do zrozumienia, ale czasami okazuje się najbardziej skomplikowana w realizacji, właśnie ze względu na jej losowy charakter.
Jak wykonać proste losowe pobieranie próbek
Procedura prostego losowego pobierania próbek jest następująca:
- Zrób listę wszystkich elementów populacji.
- Przypisz numer kolejny (1, 2, 3,…, n) każdemu elementowi populacji.
- Ustaw żądaną wielkość próbki .
- Użyj generatora liczb losowych , aby wygenerować tyle liczb, ile wynosi wybrana wielkość próby.
- Osoby przypisane do wygenerowanych liczb to osoby wybrane do próby.
Aby wygenerować liczby losowe, istnieje kilka metod, najbardziej tradycyjne to metoda loteryjna i metoda tabeli liczb:
- Metoda loterii polega na umieszczeniu wszystkich liczb w pudełku, przetasowaniu ich, a następnie losowaniu liczb.
- Metoda tabeli liczb polega na losowym wybieraniu liczb z tabeli zawierającej wszystkie możliwe liczby.
Chociaż można również zastosować dowolną z dwóch poprzednich metod, wymagają one więcej czasu i lepiej nadają się do mniejszych próbek. Obecnie do szybszego generowania liczb losowych służą programy komputerowe , można na przykład skorzystać z programu Excel.
Z drugiej strony należy wziąć pod uwagę, że wielkość próby musi być odpowiednia, aby uzyskać minimalny możliwy błąd próbkowania. Znalezienie idealnej wielkości próbki nie jest proste; Jeśli masz co do tego jakiekolwiek wątpliwości, możesz poszukać na naszej stronie artykułu, w którym wyjaśniamy, jak to zrobić.
Prosty przykład losowego pobierania próbek
Kiedy już zapoznamy się z definicją prostego próbkowania losowego, zobaczymy rozwiązany przykład przeprowadzania tego typu próbkowania.
Przykładowo, jeśli w firmie jest 2000 pracowników i chcemy przeprowadzić badanie statystyczne na próbie 400 pracowników, aby w drodze losowania prostego wybrać osoby, które wejdą do próby, w pierwszej kolejności należy: przypisanie każdemu pracownikowi numeru od 1 do 2000.
Po przypisaniu liczb musimy losowo wybrać 400 liczb. W tym przypadku wielkość próby jest dość duża, dlatego najlepiej jest skorzystać z oprogramowania komputerowego, takiego jak Excel.
Następnie do badania zostanie wybranych 400 pracowników, których przydzielona liczba została ustalona w poprzednim kroku.
W tym przykładzie uznano, że 400 pozycji stanowi wystarczająco reprezentatywną wielkość próby, ale logicznie rzecz biorąc, liczba ta będzie się zmieniać w zależności od eksperymentu.
Rodzaje prostego próbkowania losowego
Istnieją dwa rodzaje prostego pobierania próbek losowych:
- Próbkowanie losowe proste z zastępowaniem : zwracany jest wybrany element operatu losowania i można go wybrać ponownie.
- Proste pobieranie losowego bez zastępowania : element wybrany jako część próbki zostaje usunięty i nie można go już wybrać.
Dobór losowy prosty z zastępowaniem jest najprostszym rodzajem doboru próby, ponieważ w celu wybrania elementu z próby zawsze powtarza się dokładnie ten sam proces. Jednakże proste losowe pobieranie próbek bez zastępowania jest szerzej stosowane, ponieważ jest bardziej precyzyjne. Obydwa typy opisano bardziej szczegółowo poniżej.
Proste losowe pobieranie próbek z zastępowaniem
Dobór losowy prosty ze zastępowaniem polega na powrocie każdej wybranej pozycji do operatu losowania, tak aby istniała możliwość jej ponownego wybrania.
Istnieje zatem możliwość uzyskania próbki z tym samym elementem wybranym wielokrotnie, choć jest to oczywiście bardzo mało prawdopodobne.
Matematycznie jest to bardzo prosty rodzaj pobierania próbek, ponieważ prawdopodobieństwa każdej ekstrakcji są takie same. Z tego powodu zwykle rozpoczyna się naukę tej techniki próbkowania przed innymi.
W prostym doborze losowym z zastępowaniem prawdopodobieństwo otrzymania próbki o określonej kolejności można obliczyć za pomocą następującego wzoru:
![]()
Być
![]()
całkowita liczba elementów populacji i
![]()
liczba niezależnych ekstrakcji, które zostaną wykonane.
Natomiast gdy kolejność nie ma znaczenia, prawdopodobieństwo otrzymania próbki oblicza się za pomocą następującego wyrażenia:
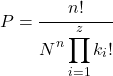
Złoto
![]()
to liczba niezależnych ekstrakcji,
![]()
liczba różnych elementów w próbce i
![]()
ile razy chcesz, aby element się pojawił
![]()
w próbce.
Na koniec, aby znaleźć prawdopodobieństwo włączenia elementu
![]()
, czyli prawdopodobieństwo włączenia elementu
![]()
W przykładzie należy zastosować następującą formułę:
![]()
Proste losowe pobieranie próbek bez zastępowania
Dobór losowy prosty bez zastępowania polega na wybraniu z próby takiej liczby osobników, na ile wskazuje pożądana wielkość próby, tak aby po wybraniu żadna osoba nie mogła zostać wybrana ponownie. Dlatego każdy wybrany element jest usuwany, a nie zastępowany.
Kiedy mówimy o prostym próbkowaniu losowym, zwykle mamy na myśli próbkę, w której poszczególne osoby nie są zastępowane, ponieważ jest to metoda najczęściej stosowana w praktyce.
Aby określić prawdopodobieństwo otrzymania próbki o określonej kolejności w prostym doborze losowym ze zastępowaniem, stosuje się następujący wzór:
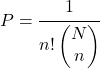
Być
![]()
całkowita liczba elementów w populacji i
![]()
liczba zależnych ekstrakcji do wykonania.
Jeżeli natomiast nie należy brać pod uwagę kolejności pobrania, prawdopodobieństwo otrzymania próbki wynosi:
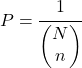
Na koniec prawdopodobieństwo włączenia elementu do prostego losowania bez zastępowania oblicza się, stosując regułę Laplace’a:
![]()
Zalety i wady prostego próbkowania losowego
Proste losowe pobieranie próbek ma następujące zalety i wady:
| korzyść | Niedogodności |
|---|---|
| Łatwy do zrozumienia. | Niezbędna jest lista wszystkich elementów populacji. |
| Wszystkie możliwe próbki są jednakowo prawdopodobne. | Może to być bardzo kosztowne w przypadku dużych próbek. |
| Zwykle uzyskuje się reprezentatywne próbki. | Zwykle charakteryzuje się większymi błędami próbkowania. |
| Do pobrania próbek nie jest wymagana żadna wiedza techniczna. | Nie wykorzystuje się wiedzy, jaką badacz może posiadać w badanym obszarze. |
| Pozwala szybko obliczyć średnie i odchylenia. | Próbka może nie być reprezentatywna, jeśli jest zbyt mała. |
| Istnieje oprogramowanie statystyczne do analizy danych. | Nie nadaje się na studia wymagające indywidualnych rozmów kwalifikacyjnych. |
Jak widzieliśmy, jedną z głównych cech prostego próbkowania losowego jest to, że jest łatwe do zrozumienia i wyjaśnienia. Rzeczywiście osoba pobierająca próbki nie musi być ekspertem w dziedzinie analiz. Jest to jednak zarówno mocna, jak i słaba strona, ponieważ w przypadku innych typów próbkowania można wykorzystać wiedzę analityka w celu uzyskania lepszego próbkowania.
Podobnie, ponieważ próbkowanie jest losowe, prawdopodobieństwo uznania tego czy innego elementu za badaną próbkę jest jednakowo prawdopodobne, w przeciwieństwie do innych rodzajów próbkowania.
Chociaż zwykle uzyskuje się reprezentatywne próbki populacji, błąd próbkowania w przypadku prostego losowego doboru próby jest duży w porównaniu z innymi rodzajami doboru próby. Ponadto próbka może nie być nawet reprezentatywna, jeśli wielkość osobników jest niewielka.
Bardzo atrakcyjną właściwością prostego doboru losowego jest to, że można go przeprowadzić za pomocą programów komputerowych, co pozwala na szybkie przeprowadzenie obliczeń statystycznych.
Na koniec należy zauważyć, że prosty dobór losowy może być droższy niż inne rodzaje doboru próby, szczególnie w szeroko rozproszonych populacjach, ponieważ może wymagać zaangażowania większych zasobów na badania. Na przykład, ponieważ jest to dobór losowy, osoby wybrane do przeprowadzenia badania mogą być bardzo rozproszone geograficznie, w związku z czym przeprowadzenie wywiadów bezpośrednich byłoby znacznie droższe.