Jak skonstruować przedział przewidywania w programie excel

W statystyce prosta regresja liniowa jest techniką, którą możemy zastosować do ilościowego określenia związku między zmienną predykcyjną x i zmienną odpowiedzi y.

Kiedy przeprowadzamy prostą regresję liniową, otrzymujemy „linię najlepszego dopasowania”, która opisuje relację między x i y, co można zapisać jako:

ŷ = b ₀ + b ₁ x

Złoto:

• ŷ jest przewidywaną wartością zmiennej odpowiedzi
• b ₀ jest punktem przecięcia z y
• b ₁ jest współczynnikiem regresji
• x jest wartością zmiennej predykcyjnej

Czasami chcemy użyć tej linii najlepszego dopasowania do skonstruowania przedziału przewidywania dla danej wartości x ₀ , który jest przedziałem wokół przewidywanej wartości × ₀ takim, że istnieje 95% prawdopodobieństwo, że prawdziwa wartość y w populacji odpowiadający x ₀ jest zawarty w tym przedziale.

Zapisuje się wzór na obliczenie przedziału predykcji dla danej wartości x ₀ :

ŷ ₀ +/- t _α/2,df=n-2 * se

Złoto:

se = S _yx √(1 + 1/n + (x ₀ – x ) ² /SS _x )

Formuła może wydawać się nieco onieśmielająca, ale w rzeczywistości można ją łatwo obliczyć w programie Excel. Następnie zobaczymy przykład użycia tej formuły do obliczenia przedziału przewidywania dla danej wartości w programie Excel.

Przykład: Jak skonstruować przedział przewidywania w programie Excel

Poniższy zbiór danych przedstawia liczbę godzin nauki oraz wynik egzaminu uzyskany przez 15 różnych uczniów:

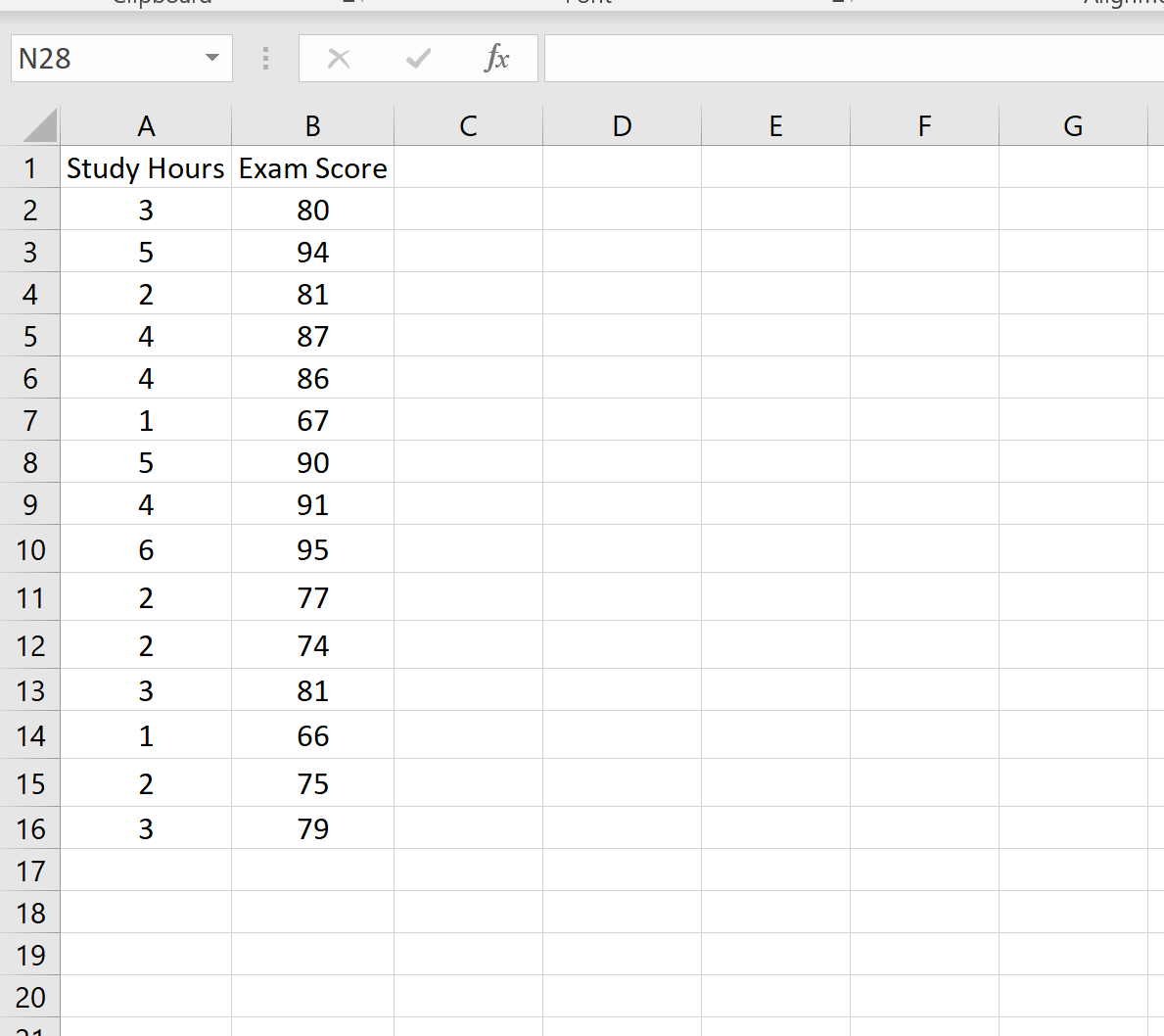
Załóżmy, że chcemy utworzyć 95% przedział przewidywań dla wartości x ₀ = 3. Oznacza to, że chcemy utworzyć taki przedział, aby istniało 95% prawdopodobieństwo, że wynik egzaminu będzie mieścić się w tym przedziale dla studenta studiującego 3 godziny.

Poniższy zrzut ekranu pokazuje, jak obliczyć wszystkie wartości potrzebne do uzyskania tego przedziału predykcji.

Uwaga: Wzory w kolumnie F pokazują, jak obliczono wartości w kolumnie E.

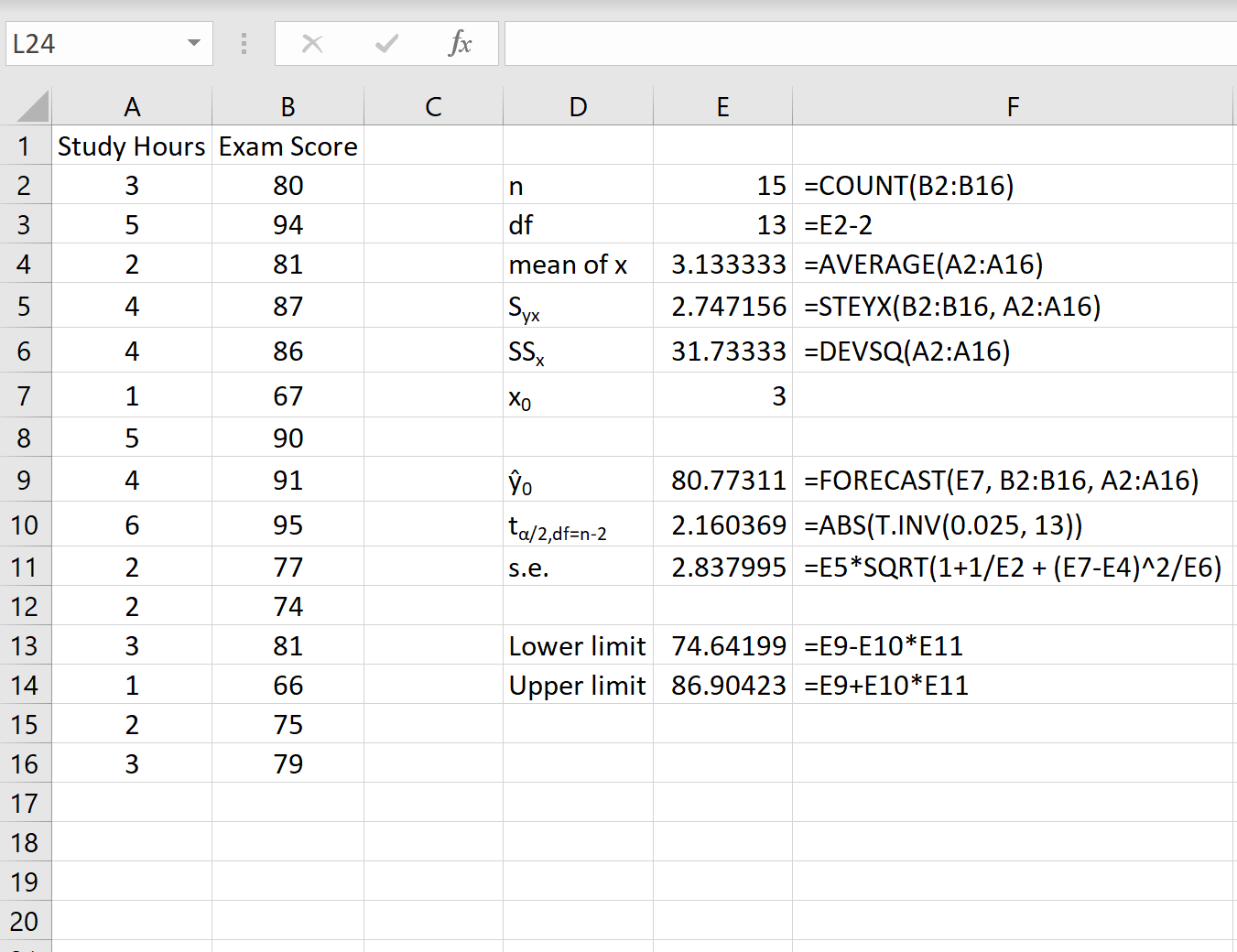
95% przedział przewidywania dla wartości x ₀ = 3 wynosi (74,64; 86,90) . Oznacza to, że z 95% prawdopodobieństwem przewidujemy, że student studiujący 3 godziny uzyska wynik pomiędzy 74,64 a 86,90.

Kilka uwag na temat zastosowanych obliczeń:

• Aby obliczyć wartość krytyczną t t _α/2,df=n-2, użyliśmy α/2 = 0,05/2 = 0,25, ponieważ chcieliśmy przedziału predykcji wynoszącego 95%. Należy zauważyć, że wyższe przedziały przewidywania (np. 99% przedział przewidywania) prowadzą do szerszych przedziałów. I odwrotnie, mniejszy przedział przewidywania (np. 90% przedział przewidywania) będzie prowadził do węższego przedziału.
• Użyliśmy wzoru =PROGNOZA() , aby uzyskać przewidywaną wartość dla ŷ ₀ , ale formuła =PROGNOZA.LINEAR() zwróci dokładnie tę samą wartość.