Jak obliczyć przedziały ufności w sas-ie

Przedział ufności to zakres wartości, który prawdopodobnie będzie zawierał parametr populacji z pewnym poziomem ufności.

W tym samouczku wyjaśniono, jak obliczyć następujące przedziały ufności w R:

1. Przedział ufności dla średniej populacji

2. Przedział ufności dla różnicy średnich z populacji

Chodźmy!

Przykład 1: Przedział ufności dla średniej populacji w SAS

Załóżmy, że mamy następujący zestaw danych zawierający wysokość (w calach) losowej próbki 12 roślin należących do tego samego gatunku:

 /*create dataset*/
data my_data;
    inputHeight ;
    datalines ;
14
14
16
13
12
17
15
14
15
13
15
14
;
run ;

/*view dataset*/
proc print data =my_data; 

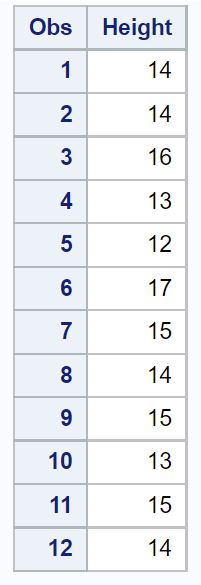
Załóżmy, że chcemy obliczyć 95% poziom ufności dla prawdziwej średniej wielkości populacji tego gatunku.

W tym celu możemy użyć następującego kodu w SAS-ie:

 /*generate 95% confidence interval for population mean*/
proc ttest data =my_data alpha = 0.05 ;
    varHeight ;
run ;

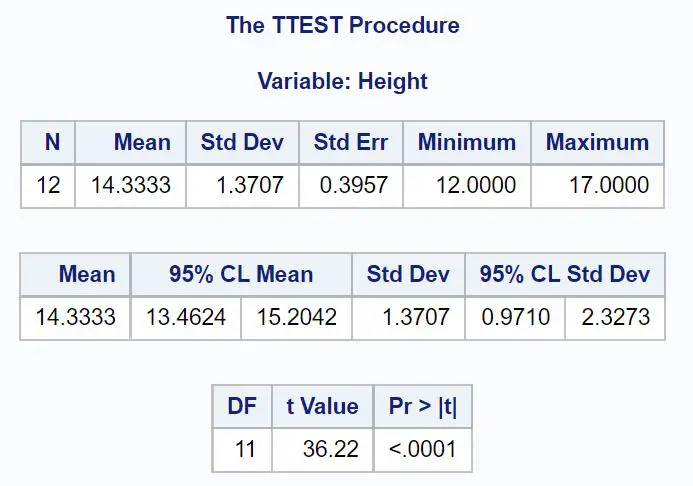
Wartość średniej wskazuje średnią próbki, a wartości mniejsze niż 95% CL Mean pokazują 95% przedział ufności dla średniej populacji.

Z wyników widzimy, że 95% przedział ufności dla średniej masy rośliny w tej populacji wynosi [13,4624 cala, 15,2042 cala] .

Przykład 2: Przedział ufności dla różnicy średnich populacji w SAS

Załóżmy, że mamy następujący zbiór danych zawierający wysokość (w calach) losowej próbki roślin należących do dwóch różnych gatunków:

 /*create dataset*/
data my_data2;
    input Species $Height;
    datalines ;
At 14
At 14
At 16
At 13
AT 12
At 17
At 15
At 14
At 15
At 13
B15
B14
B 19
B 19
B17
B 18
B20
B 19
B17
B15
;
run ;

/*view dataset*/
proc print data =my_data2; 

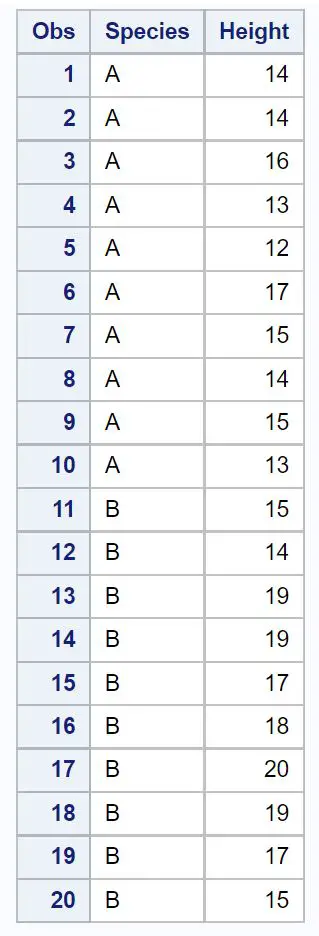
Załóżmy, że chcemy obliczyć 95% poziom ufności dla różnicy w średniej wielkości populacji między gatunkami A i gatunkami B.

W tym celu możemy użyć następującego kodu w SAS-ie:

 /*sort data by Species to ensure confidence interval is calculated correctly*/
proc sort data =my_data2;
    by Species;
run ;

/*generate 95% confidence interval for difference in population means*/
proc ttest data =my_data2 alpha = 0.05 ;
    class Species;
    varHeight ;
run ;

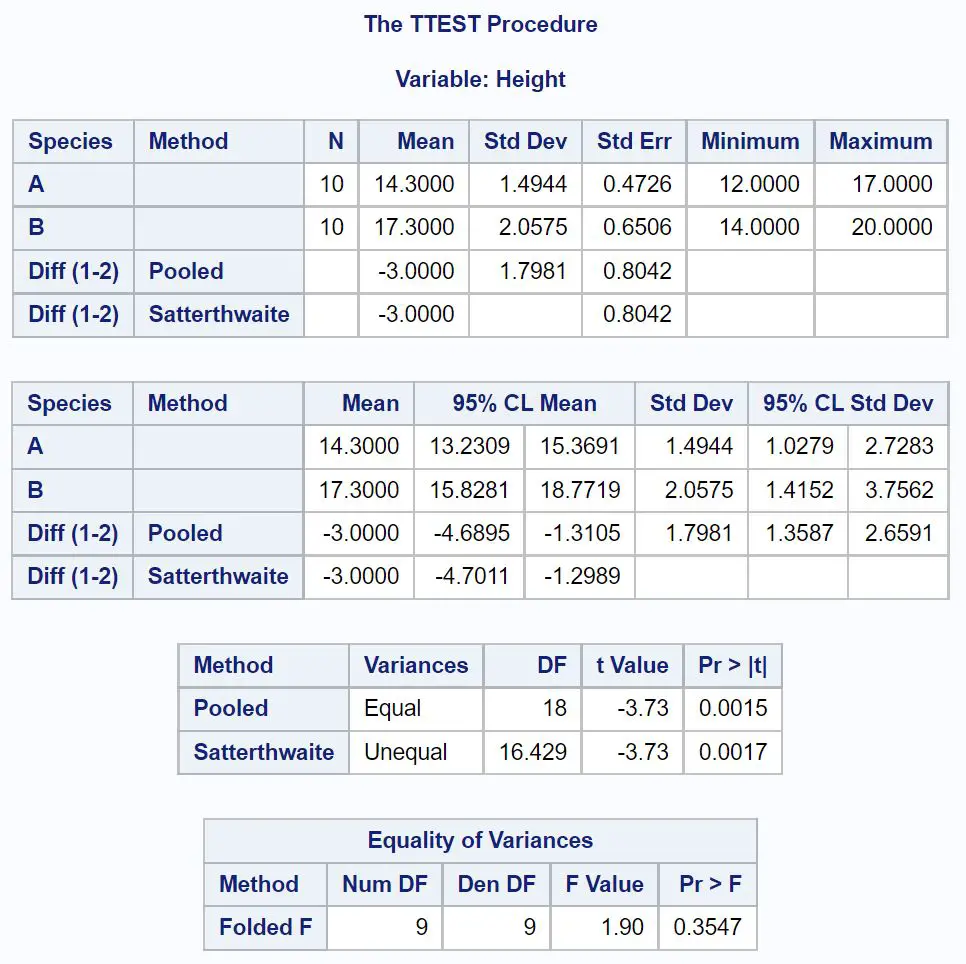
Pierwszą tabelą, na którą musimy zwrócić uwagę w wynikach, jest Równość wariancji , która sprawdza, czy wariancja między każdą próbą jest równa, czy nie.

Ponieważ wartość p w tej tabeli jest nie mniejsza niż 0,05, możemy założyć, że różnice między obiema grupami są równe.

Możemy więc spojrzeć na linię wykorzystującą łączną wariancję do znalezienia 95% przedziału ufności dla różnicy średnich z populacji.

Z wyniku widzimy, że 95% przedział ufności dla różnicy między średnimi z populacji wynosi [-4,6895 cala, -1,1305 cala] .

To mówi nam, że możemy być pewni w 95%, że prawdziwa różnica między średnią wysokością roślin gatunku A i gatunku B wynosi od -4,6895 cala do -1,1305 cala.

Ponieważ0 nie mieści się w tym przedziale ufności , oznacza to, że istnieje statystycznie istotna różnica między średnimi z obu populacji.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w SAS-ie:

Jak wykonać test t dla jednej próby w SAS
Jak wykonać test t dla dwóch próbek w SAS
Jak wykonać test t dla sparowanych próbek w SAS