Jak obliczyć przedziały ufności w programie excel
Przedział ufności to zakres wartości, który prawdopodobnie będzie zawierał parametr populacji z pewnym poziomem ufności. Oblicza się go według następującego ogólnego wzoru:
Przedział ufności = (oszacowanie punktowe) +/- (wartość krytyczna)* (błąd standardowy)
Ta formuła tworzy przedział z dolną i górną granicą, który prawdopodobnie zawiera parametr populacji z pewnym poziomem ufności:
Przedział ufności = [dolna granica, górna granica]
W tym samouczku wyjaśniono, jak obliczyć następujące przedziały ufności w programie Excel:
1. Przedział ufności dla średniej
2. Przedział ufności dla różnicy średnich
3. Przedział ufności dla proporcji
4. Przedział ufności dla różnicy proporcji
Chodźmy!
Przykład 1: Przedział ufności dla średniej
Do obliczenia przedziału ufności dla średniej używamy następującego wzoru:
Przedział ufności = x +/- z*(s/√n)
Złoto:
- x : przykładowe środki
- z: wybrana wartość z
- s: odchylenie standardowe próbki
- n: wielkość próbki
Przykład: Załóżmy, że zbieramy losową próbkę żółwi z następującymi informacjami:
- Wielkość próby n = 25
- Średnia masa próbki x = 300
- Próbka odchylenie standardowe s = 18,5
Poniższy zrzut ekranu pokazuje, jak obliczyć 95% przedział ufności dla prawdziwej średniej masy populacji żółwi:
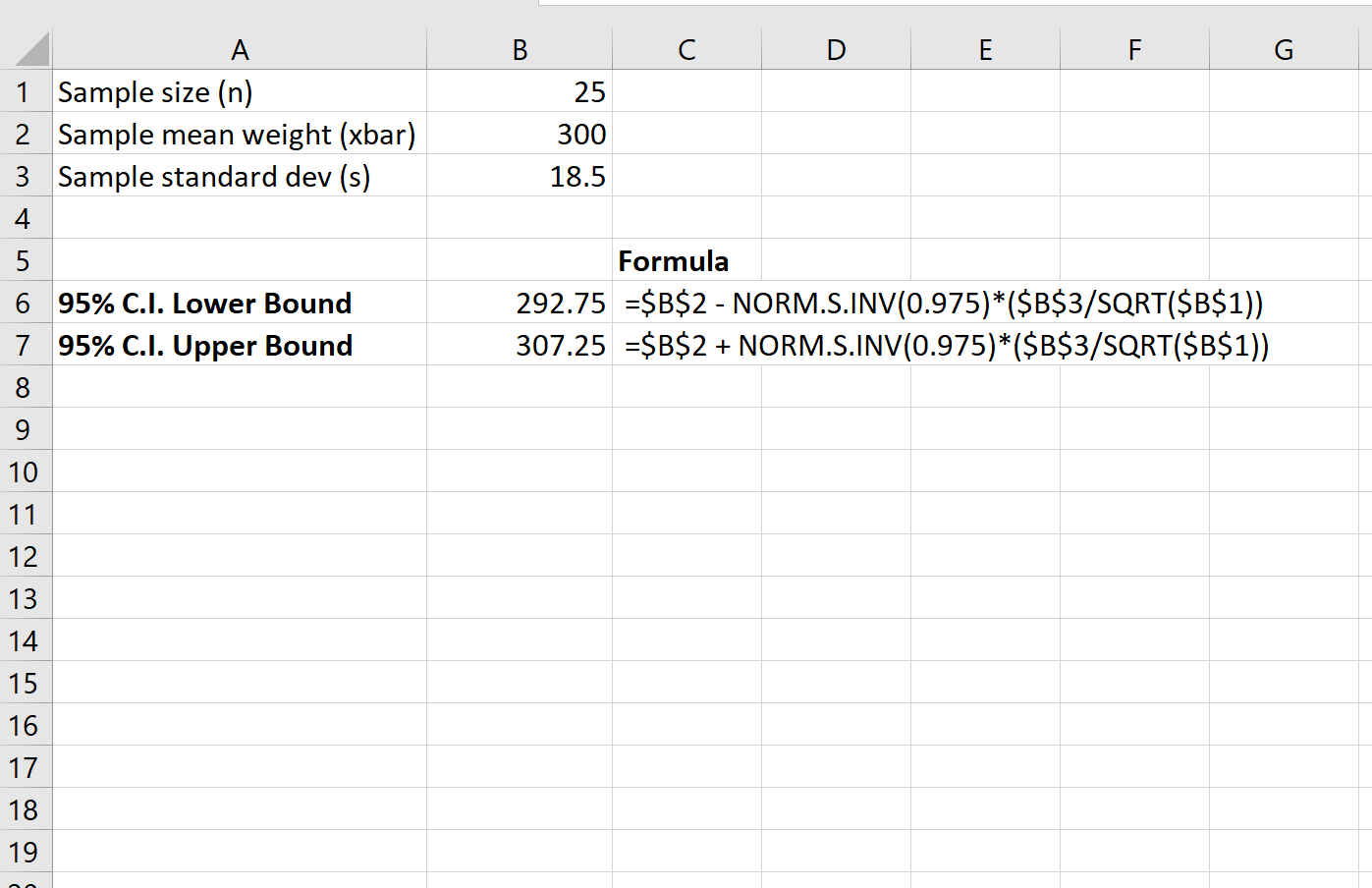
95% przedział ufności dla prawdziwej średniej masy populacji żółwi wynosi [292,75, 307,25] .
Przykład 2: Przedział ufności dla różnicy średnich
Do obliczenia przedziału ufności dla różnicy średnich populacji stosujemy następujący wzór:
Przedział ufności = ( x 1 – x 2 ) +/- t*√((s p 2 /n 1 ) + (s p 2 /n 2 ))
Złoto:
- x 1 , x 2 : średnia z próbki 1, średnia z próbki 2
- t: wartość krytyczna t oparta na poziomie ufności i (n 1 + n 2 -2) stopniach swobody
- s p 2 : wariancja zbiorcza, obliczona jako ((n 1 -1) s 1 2 + (n 2 -1) s 2 2 ) / (n 1 + n 2 -2)
- t: wartość krytyczna t
- n 1 , n 2 : wielkość próby 1, wielkość próby 2
Przykład: Załóżmy, że chcemy oszacować różnicę w średniej masie dwóch różnych gatunków żółwi. Dlatego pobieramy losową próbkę 15 żółwi z każdej populacji. Oto podsumowanie danych dla każdej próbki:
Próbka 1:
- x1 = 310
- s 1 = 18,5
- n 1 = 15
Próbka 2:
- x2 = 300
- s2 = 16,4
- n2 = 15
Poniższy zrzut ekranu pokazuje, jak obliczyć 95% przedział ufności dla prawdziwej różnicy średnich z populacji:
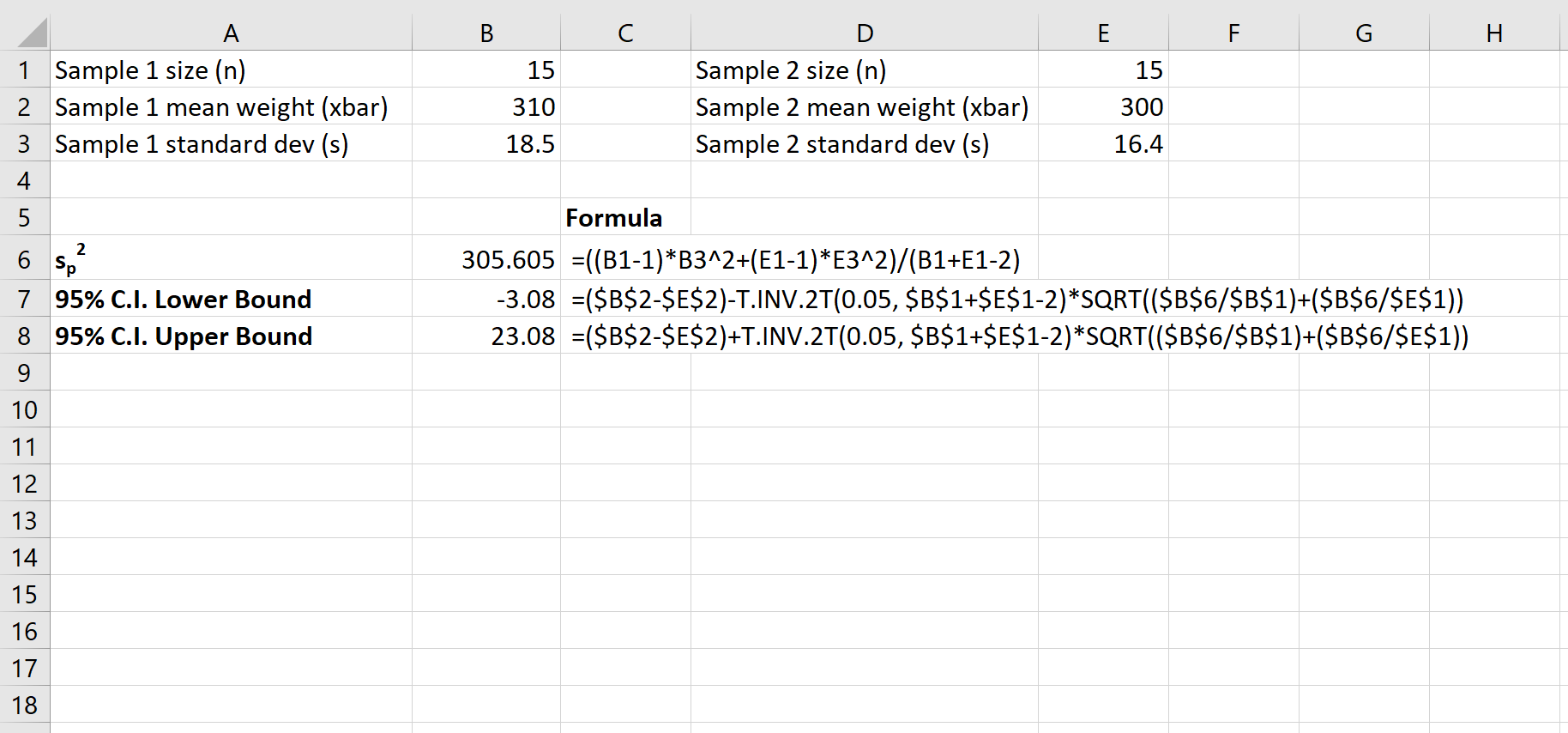
95% przedział ufności dla prawdziwej różnicy między średnimi populacji wynosi [-3,08; 23,08] .
Przykład 3: Przedział ufności dla proporcji
Do obliczenia przedziału ufności dla proporcji używamy następującego wzoru:
Przedział ufności = p +/- z*√ p(1-p) / n
Złoto:
- p: proporcja próbki
- z: wybrana wartość z
- n: wielkość próbki
Przykład: Załóżmy, że chcemy oszacować odsetek mieszkańców hrabstwa, którzy opowiadają się za określonym prawem. Wybieramy losową próbę 100 mieszkańców i pytamy ich, jakie jest ich stanowisko w świetle prawa. Oto wyniki:
- Wielkość próby n = 100
- Proporcja na korzyść prawa p = 0,56
Poniższy zrzut ekranu pokazuje, jak obliczyć 95% przedział ufności dla prawdziwego odsetka mieszkańców całego hrabstwa, którzy opowiadają się za prawem:
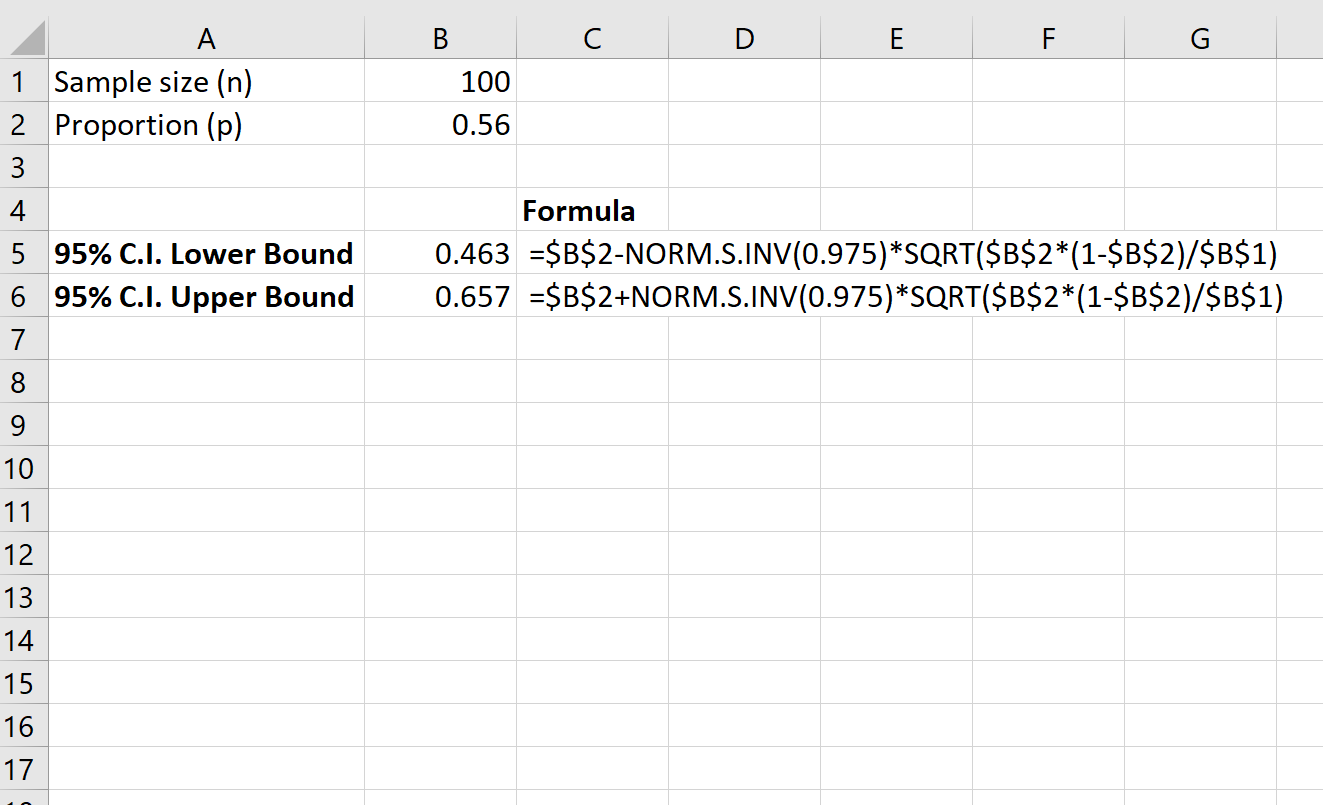
95% przedział ufności dla prawdziwego odsetka mieszkańców całego hrabstwa, którzy opowiadają się za prawem, wynosi [0,463, 0,657] .
Przykład 4: Przedział ufności dla różnicy proporcji
Do obliczenia przedziału ufności dla różnicy proporcji używamy następującego wzoru:
Przedział ufności = (p 1 –p 2 ) +/- z*√(p 1 (1-p 1 )/n 1 + p 2 (1-p 2 )/n 2 )
Złoto:
- p 1 , p 2 : proporcja próbki 1, proporcja próbki 2
- z: wartość krytyczna z oparta na poziomie ufności
- n 1 , n 2 : wielkość próby 1, wielkość próby 2
Przykład: Załóżmy, że chcemy oszacować różnicę między odsetkiem mieszkańców popierających określone prawo w hrabstwie A w porównaniu z odsetkiem popierającym prawo w hrabstwie B. Oto podsumowanie danych dla każdej próby:
Próbka 1:
- n 1 = 100
- p 1 = 0,62 (tj. 62 mieszkańców na 100 popiera ustawę)
Próbka 2:
- n2 = 100
- p 2 = 0,46 (tj. 46 mieszkańców na 100 popiera ustawę)
Poniższy zrzut ekranu pokazuje, jak obliczyć 95% przedział ufności dla prawdziwej różnicy w odsetku mieszkańców popierających prawo pomiędzy powiatami:
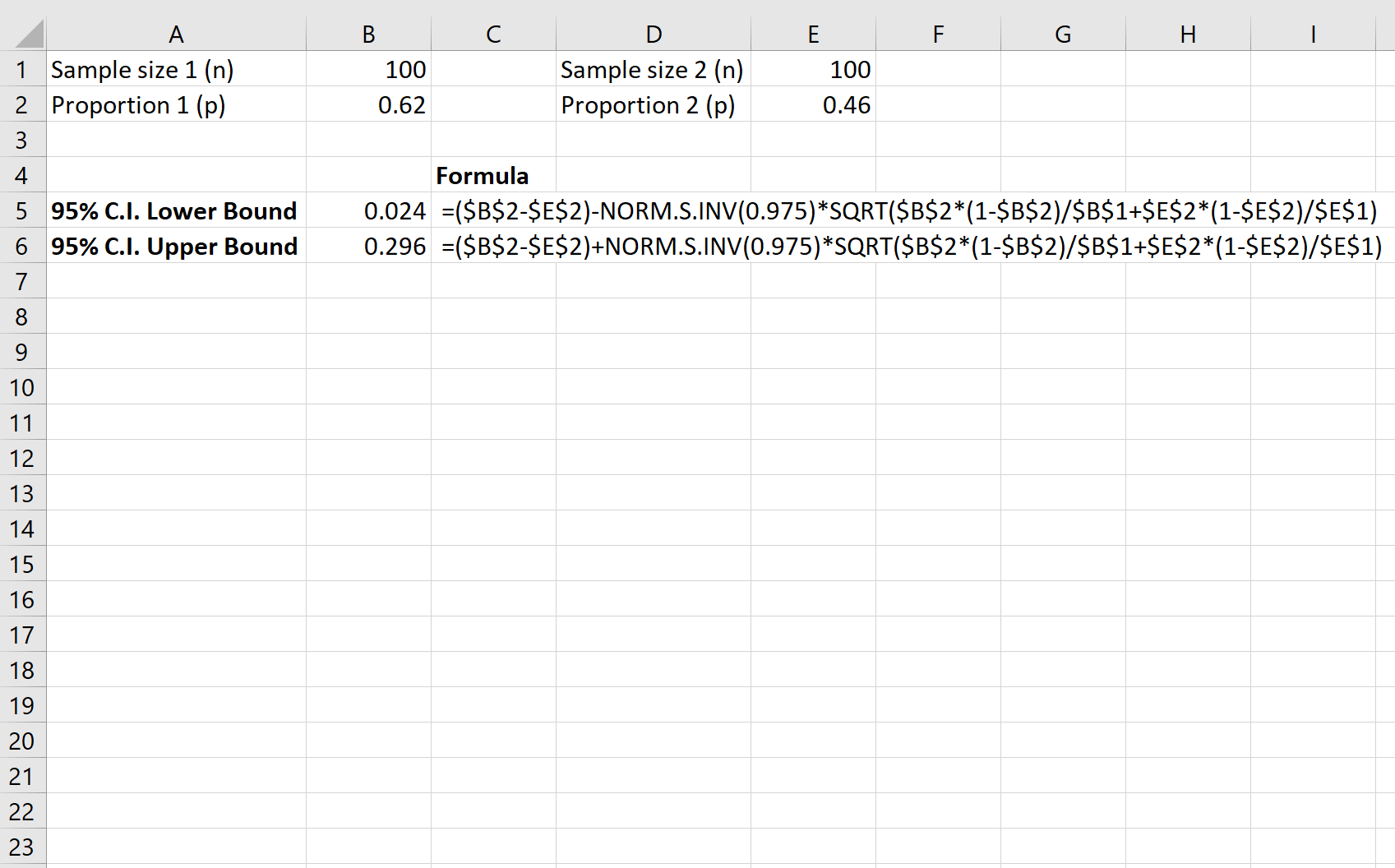
9,5% przedział ufności dla prawdziwej różnicy w odsetku mieszkańców popierających prawo pomiędzy powiatami wynosi [0,024; 0,296] .
Więcej samouczków dotyczących Excela znajdziesz tutaj .
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej