Jak konwertować wyniki z i percentyle w programie excel

Wynik z mówi nam, ile odchyleń standardowych ma dana wartość od średniej zbioru danych.

Percentyl mówi nam, jaki procent obserwacji spada poniżej określonej wartości w zbiorze danych.

Często chcemy dokonać konwersji między wynikami Z i percentylami, w zależności od rodzaju pytania, na które staramy się odpowiedzieć. Na szczęście Excel ma dwie wbudowane funkcje, które ułatwiają konwersję między nimi.

Jak przekonwertować wyniki Z na percentyle w programie Excel

Możemy użyć następującej wbudowanej funkcji programu Excel, aby przekonwertować wynik az na percentyl:

= ROZKŁAD.NORMALNY(z, skumulowany)

Złoto:

• z = wynik z określonej wartości danych
• skumulowany = PRAWDA zwraca funkcję rozkładu skumulowanego; FAŁSZ zwraca funkcję rozkładu prawdopodobieństwa. Do obliczenia percentyli użyjemy wartości TRUE.

Na przykład, oto jak przekonwertować wynik Z wynoszący 1,78 na percentyl:

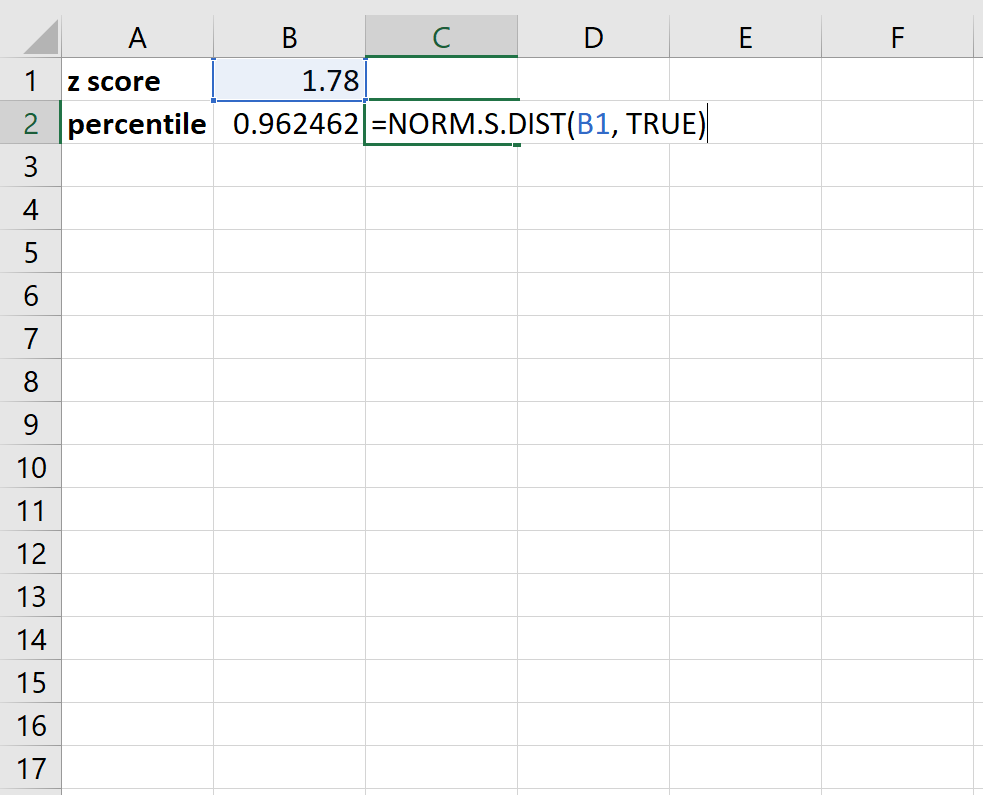
Okazuje się, że wynik z wynoszący 1,78 odpowiada percentylowi wynoszącemu w przybliżeniu 96,2 . W prostym języku angielskim oznacza to, że wartość danych o wyniku Z wynoszącym 1,78 jest większa niż około 96,2% wszystkich innych wartości danych w zbiorze danych.

Jak przekonwertować percentyle na wyniki Z w programie Excel

Możemy użyć następującej wbudowanej funkcji programu Excel, aby przekonwertować percentyl na wynik az:

=NORMALNY.S.INV(prawdopodobieństwo)

Złoto:

• prawdopodobieństwo = percentyl, który chcesz przekonwertować.

Na przykład, oto jak przekonwertować percentyl 0,85 na wynik Z:

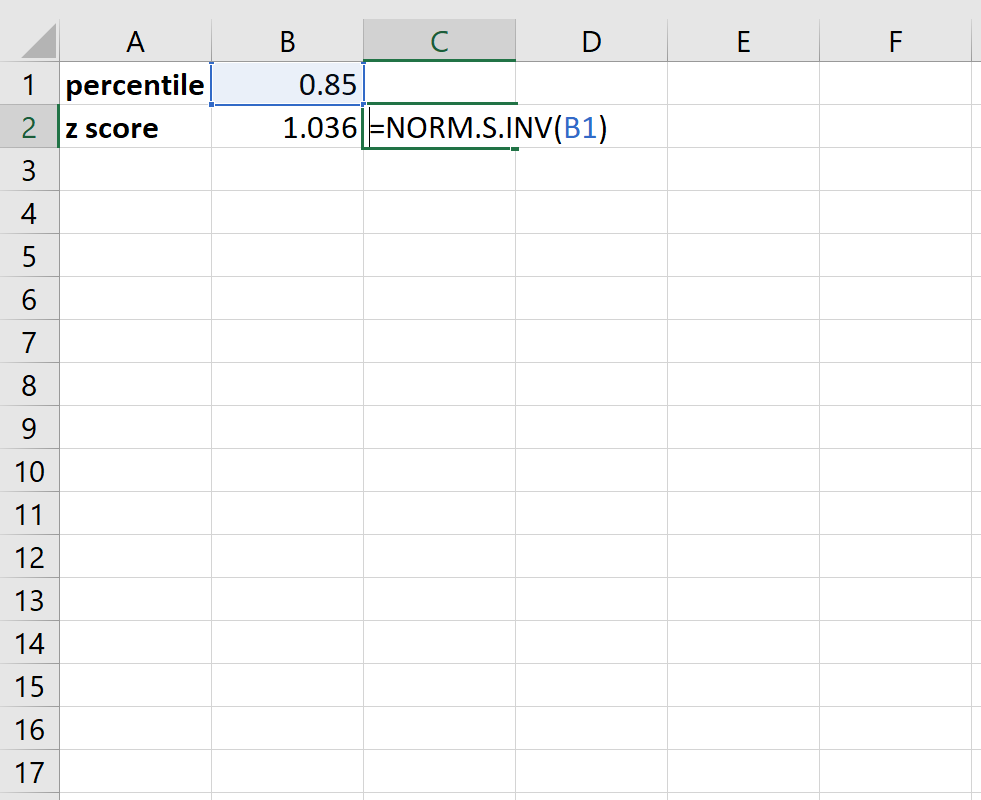
Okazuje się, że percentyl 0,85 odpowiada wynikowi Z wynoszącemu około 1,036 . Mówiąc wprost, oznacza to, że wartość danych na 85. percentylu w zbiorze danych ma wynik z wynoszący 1,036.

Zależność między percentylami a wynikami Z

Wyniki Z mogą przyjmować dowolną wartość pomiędzy ujemną nieskończonością a nieskończonością. Jednak percentyle mogą przyjmować tylko wartości z zakresu od 0 do 100.

Wynik Z wynoszący 0 odpowiada percentylowi wynoszącemu dokładnie 0,50. Zatem każdy wynik z większy niż 0 odpowiada percentylowi większemu niż 0,50, a każdy wynik z mniejszy niż 0 odpowiada percentylowi mniejszemu niż 0,50.

W zależności od rodzaju pytania, na które próbujesz odpowiedzieć, bardziej przydatna może być znajomość wyniku Z lub percentyla.

Załóżmy na przykład, że Jessica uzyskuje 90% z pewnego egzaminu. Może się to wydawać wysokim wynikiem, ale co by było, gdyby egzamin był naprawdę łatwy i cała jego klasa wypadła dobrze? Aby określić, jak dobra jest jego ocena w porównaniu ze wszystkimi innymi ocenami w klasie, możemy obliczyć zarówno wynik Z, jak i percentyl jego oceny z egzaminu.

Jeśli jej wynik egzaminu odpowiada punktowi Z wynoszącemu 1,23, oznacza to, że jej wynik egzaminu był o 1,23 odchylenia standardowego wyższy od średniego wyniku egzaminu. Ten wynik z odpowiada również percentylowi około 0,89, co oznacza, że uzyskała wyższy wynik niż 89% jej kolegów z klasy. Zwróć uwagę, jak wynik Z i percentyl dostarczają nam przydatnych informacji o wynikach jej egzaminu.