Co to jest przestrzeń próbna? definicja i przykłady
Przestrzeń próbki eksperymentu to zbiór wszystkich możliwych wyników eksperymentu.
Załóżmy na przykład, że rzucamy kostką raz. Przykładowa przestrzeń możliwych wyników obejmuje:
Przestrzeń próbki = 1, 2, 3, 4, 5, 6
Korzystając z notacji, zapisujemy symbol przestrzeni próbek jako kursywę S, a wyniki w nawiasach w następujący sposób:
S = {1, 2, 3, 4, 5, 6}
Przykłady przykładowych przestrzeni
Oto kilka dodatkowych przykładów przykładowych przestrzeni:
Przykład 1: losowanie
Załóżmy, że raz rzucamy monetą. Jeśli przyjmiemy, że H = moneta wyląduje na reszce i T = moneta wyląduje na reszce, wówczas przykładowa przestrzeń dla tego rzutu monetą będzie wynosić:
S = {H., T.}
Przykład 2: Kulki w torbie
Załóżmy, że losowo wybieramy kulkę z worka zawierającego trzy kulki: czerwoną, zieloną i niebieską. Jeśli przyjmiemy, że R = czerwony, G = zielony i B = niebieski, wówczas przestrzeń próbek wynosi:
S = {R, G, B}
Przykład 3: Rzut monetą i kostką
Załóżmy, że rzucamy monetą i jednocześnie rzucamy kostką. Jeśli pozwolimy, aby H1 reprezentował wynik „głowy” i „1”, wówczas przestrzeń próbna dla wyników będzie następująca:
S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}
Podstawowa zasada liczenia
Podstawową zasadą liczenia jest sposób obliczania całkowitej liczby potencjalnych wyników eksperymentu.
Zasada ta stwierdza, że jeśli zdarzenie A ma n różnych wyników, a zdarzenie B ma m różnych wyników, wówczas całkowitą liczbę potencjalnych wyników można obliczyć w następujący sposób:
Wyniki ogółem = m * n
Przykład 1: Rzut monetą i kostką
Na przykład, jeśli jednocześnie rzucimy monetą i kostką, wówczas całkowitą liczbę wyników w przestrzeni próbki można obliczyć w następujący sposób:
Suma wyników = (2 sposoby, w jakie może wylądować moneta) * (6 sposobów, w jakie może wylądować kość) = 12 możliwych wyników.
W poprzednim przykładzie napisaliśmy te 12 wyników:
S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}
Przykład 2: Liczenie kombinacji strojów
Zasadę tę można również zastosować do obliczenia całkowitych wyników w przestrzeni próbki dla więcej niż dwóch zdarzeń.
Załóżmy na przykład, że w losowej szufladzie znajdują się 3 różne koszule, 4 różne spodnie i 2 różne skarpetki. Jeśli losowo wybierzemy po jednym elemencie garderoby, bez patrzenia, łączna liczba możliwych strojów zostanie obliczona w następujący sposób:
Łączna liczba strojów = 3 * 4 * 2 = 24 możliwe stroje
Wizualizacja przykładowych przestrzeni za pomocą diagramów drzewiastych
Gdy liczba wyników w przestrzeni próbek jest duża, przydatne może być skonstruowanie diagramu drzewa w celu wizualizacji różnych kombinacji wyników.
Załóżmy na przykład, że w szafie znajdują się 2 różne koszule, 2 różne spodnie i 2 różne skarpetki. Jeśli losowo wybierzemy po jednym elemencie garderoby, bez patrzenia, całkowitą liczbę możliwych strojów można zwizualizować w następujący sposób:
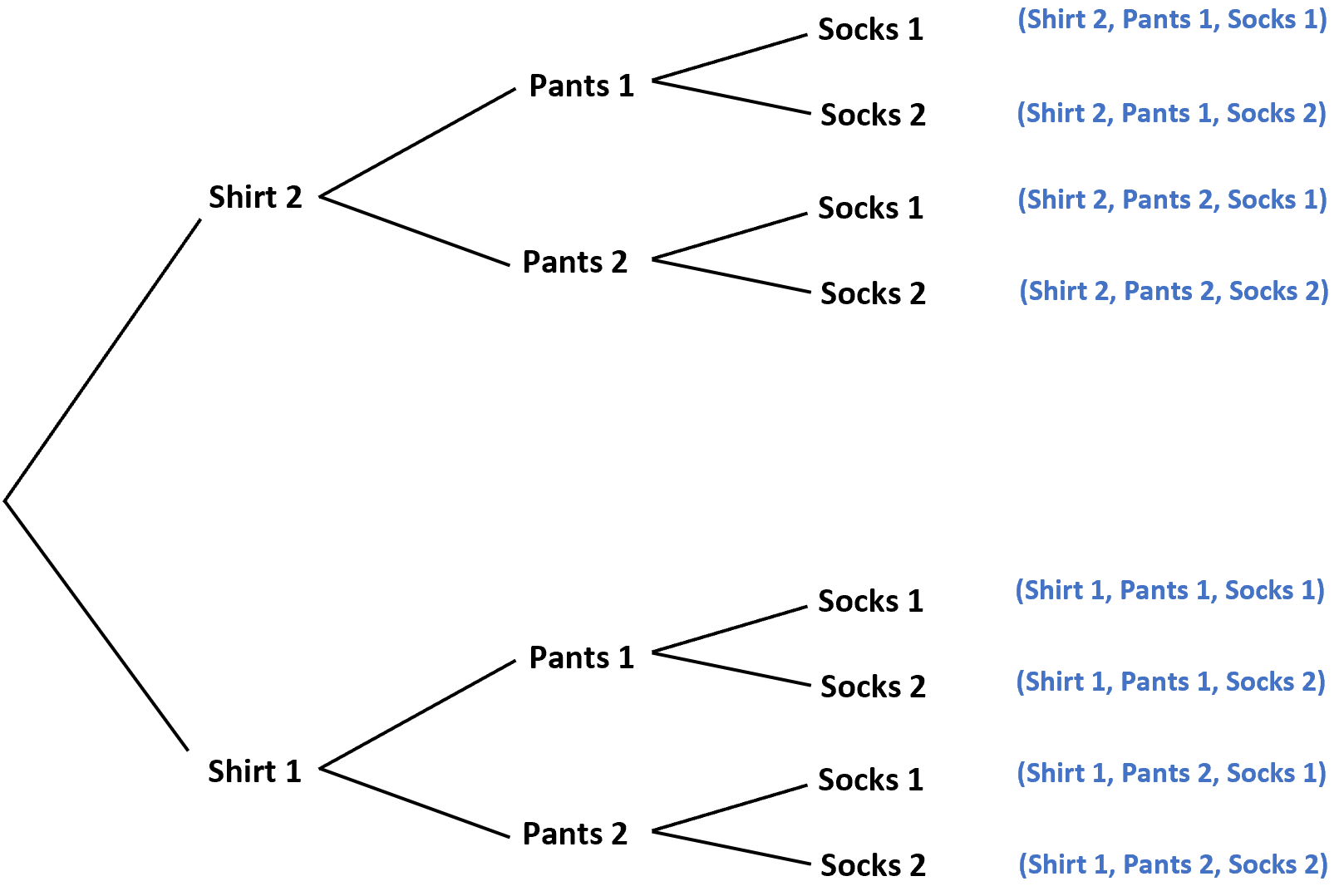
Ten diagram pomaga nam zwizualizować osiem różnych potencjalnych wyników w przestrzeni próbki.
Możemy również skorzystać z podstawowej zasady liczenia, aby potwierdzić, że musi istnieć osiem różnych wyników:
Łączne wyniki = 2 koszule * 2 spodnie * 2 skarpetki = 8 możliwych zestawów
Obliczanie prawdopodobieństw wyników w przestrzeniach próbnych
Po zidentyfikowaniu przestrzeni próbnej eksperymentu możemy obliczyć prawdopodobieństwo wystąpienia zdarzenia A , korzystając z następującego wzoru:
P(A) = (Przestrzeń próbki A) / (Całkowita przestrzeń próbki)
Załóżmy na przykład, że rzucamy kostką raz. Przestrzeń próbki można zapisać w postaci:
S = {1, 2, 3, 4, 5, 6}
Jeśli zdefiniujemy zdarzenie A jako lądowanie kostką na liczbie „2”, to przestrzeń próbną zdarzenia A można zapisać w następujący sposób:
S = {2}
Zatem prawdopodobieństwo wystąpienia zdarzenia A można obliczyć w następujący sposób:
P(A) = 1/6
Jeśli zdefiniujemy zdarzenie A jako lądowanie kostką na parzystej liczbie, to przestrzeń próbną zdarzenia A można zapisać w następujący sposób:
S = {2, 4, 6}
Zatem prawdopodobieństwo wystąpienia zdarzenia A można obliczyć w następujący sposób:
P(A) = 3/6