Jak wykonać testy t w arkuszach google

Ogólnie rzecz biorąc, istnieją trzy typy testów t:

• Próbny test t
• Test T dla dwóch próbek
• Test t dla sparowanych próbek

W tym samouczku znajdziesz przykłady wykonania każdego z tych testów w Arkuszach Google.

Przykład: test t dla jednej próby

Definicja: Test t dla jednej próby służy do sprawdzenia, czy średnia populacji jest równa określonej wartości.

Przykład: Botanik chce wiedzieć, czy średnia wysokość określonego gatunku rośliny wynosi 15 cali. Bierze losową próbkę 12 roślin i zapisuje wysokość każdej z nich w calach.

Poniższy zrzut ekranu pokazuje, jak wykonać test t dla jednej próby, aby określić, czy prawdziwy średni wzrost populacji jest równy 15 cali:

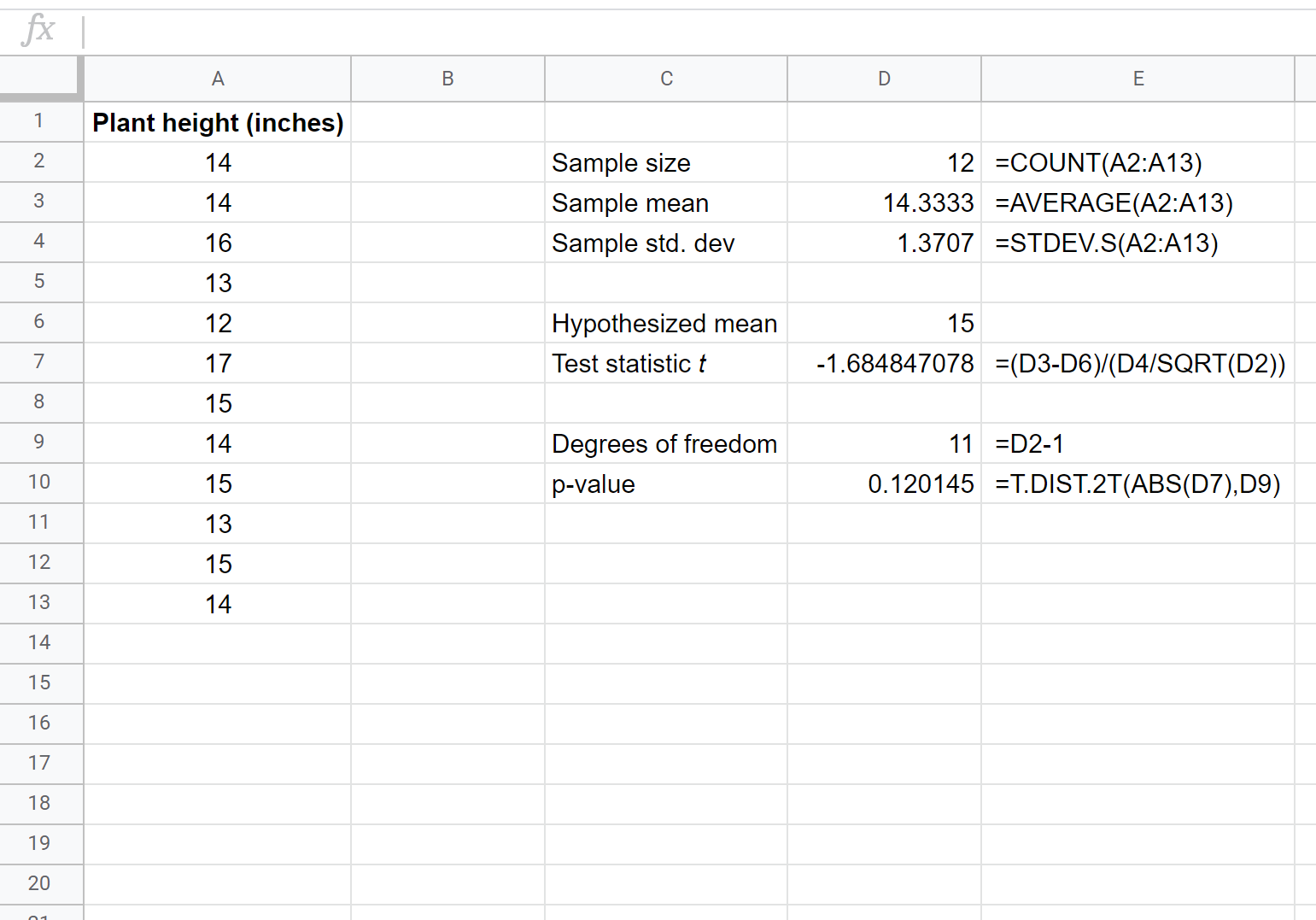
Dwie hipotezy dotyczące tego testu t na konkretnej próbie są następujące:

H ₀ : µ = 15 (średnia wysokość tego gatunku rośliny wynosi 15 cali)

H _A : µ ≠15 (średnia wysokość nie wynosi 15 cali)

Wartość p naszego testu (0,120145) jest większa niż alfa = 0,05, więc nie możemy odrzucić hipotezy zerowej testu. Nie mamy wystarczających dowodów, aby stwierdzić, że średnia wysokość tego konkretnego gatunku rośliny jest inna niż 15 cali.

Przykład: test t dla dwóch próbek

Definicja: Test t dla dwóch prób służy do sprawdzenia, czy średnie z dwóch populacji są równe, czy nie.

Przykład: Naukowcy chcą wiedzieć, czy dwa różne gatunki roślin w danym kraju mają tę samą średnią wysokość. Zbierają losową próbkę 20 roślin z każdego gatunku i rejestrują wysokość każdej rośliny w calach.

Poniższy zrzut ekranu pokazuje, jak wykonać test t dla dwóch próbek przy użyciu funkcji T.TEST() w celu ustalenia, czy średnie wzrosty w dwóch populacjach są równe:

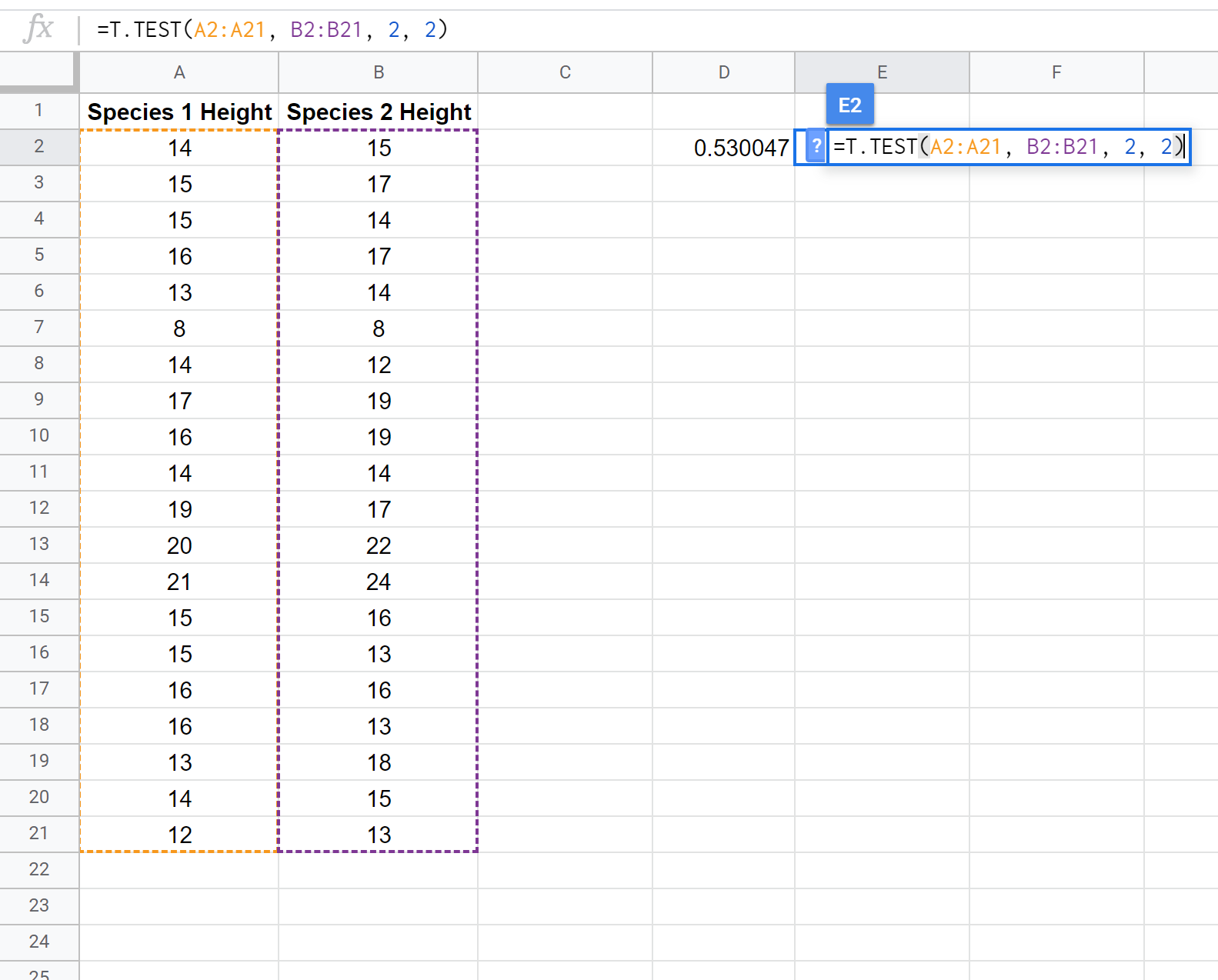
Uwaga: Możliwe jest również wykonanie jednostronnego testu t dla dwóch próbek z założeniem lub bez założenia, że obie próbki mają tę samą wariancję. Aby dowiedzieć się, jak dostosować założenia testu, zapoznaj się z dokumentacją T.TEST .

Dwie hipotezy dotyczące tego testu t dla dwóch próbek to:

H ₀ : μ ₁ = μ ₂ (średnie z obu populacji są równe)

H ₁ : μ ₁ ≠ μ ₂ (średnie z obu populacji nie są równe)

Ponieważ wartość p naszego testu (0,530047) jest większa niż alfa = 0,05, nie udało nam się odrzucić hipotezy zerowej testu. Nie mamy wystarczających dowodów, aby stwierdzić, że średnia wysokość tego konkretnego gatunku rośliny jest inna niż 15 cali.

Przykład: test t dla sparowanych próbek

Definicja: Test t dla par prób służy do porównywania średnich z dwóch próbek, gdy każdą obserwację z jednej próbki można powiązać z obserwacją z drugiej próbki.

Przykład: Chcemy wiedzieć, czy kierunek studiów ma znaczący wpływ na wyniki uczniów na konkretnym egzaminie. Aby to sprawdzić, prosimy 20 uczniów w klasie o przystąpienie do testu wstępnego. Następnie każdy z uczniów uczestniczy w programie nauczania przez dwa tygodnie. Następnie uczniowie ponownie przystępują do testu o podobnym stopniu trudności.

Poniższy zrzut ekranu pokazuje, jak wykonać test t dla par próbnych, aby porównać różnicę między średnimi wynikami pierwszego i drugiego testu:

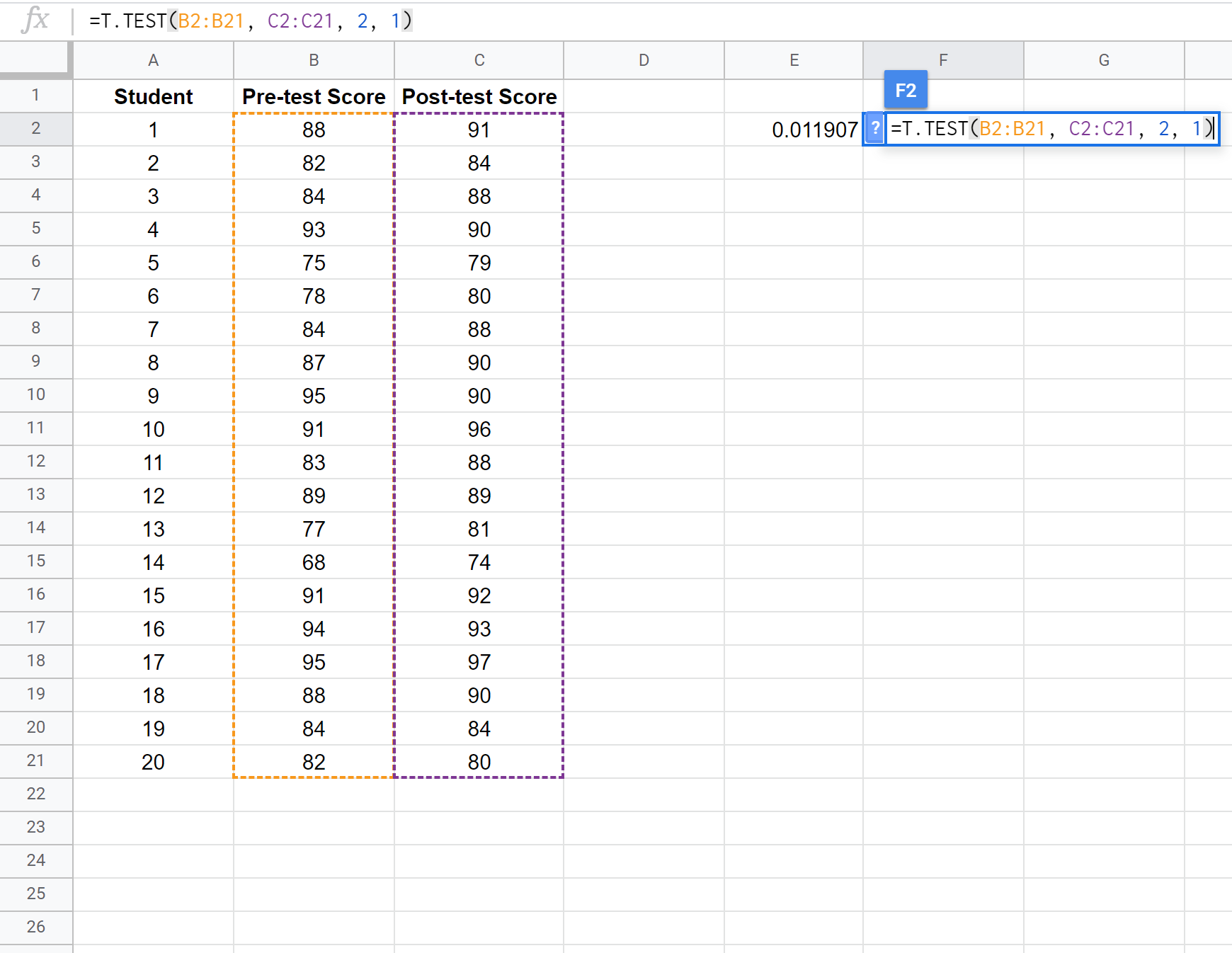
Uwaga: Możliwe jest również wykonanie jednostronnego testu t dla dwóch próbek z założeniem lub bez założenia, że obie próbki mają tę samą wariancję. Aby dowiedzieć się, jak dostosować założenia testu, zapoznaj się z dokumentacją T.TEST .

Dwa założenia tego testu t dla par próbek są następujące:

H ₀ : μ ₁ = μ ₂ (średnie z obu populacji są równe)

H ₁ : μ ₁ ≠ μ ₂ (średnie z obu populacji nie są równe)

Ponieważ wartość p naszego testu (0,011907) jest mniejsza niż alfa = 0,05, odrzucamy hipotezę zerową testu. Mamy wystarczające dowody, aby stwierdzić, że istnieje statystycznie istotna różnica pomiędzy średnim wynikiem przed i po teście.