Co to jest ocena punktowa w statystyce?
Często w statystyce interesuje nas pomiar parametrów populacji , czyli liczb opisujących pewne cechy całej populacji.
Dwa z najczęstszych parametrów populacji to:
1. Średnia populacji: średnia wartość zmiennej w populacji (na przykład średni wzrost mężczyzn w danym mieście)
2. Proporcja populacji: proporcja zmiennej w populacji (na przykład odsetek mieszkańców powiatu, którzy popierają określone prawo)
Nawet jeśli chcemy zmierzyć te parametry, gromadzenie danych na temat każdej osoby w populacji jest zazwyczaj zbyt kosztowne i czasochłonne.
Zamiast tego pobieramy losową próbkę z populacji i wykorzystujemy próbne dane do oszacowania parametru populacji.
Liczba, której używamy w próbie do oszacowania parametru populacji, nazywa się estymacją punktową . Jest to nasze najlepsze możliwe oszacowanie prawdziwego parametru populacji.
Poniższa tabela przedstawia estymację punktową, której używamy do estymacji parametrów populacji:
| Pomiar | Parametr populacji | Punktowe oszacowanie |
|---|---|---|
| Mieć na myśli | μ (średnia populacji) | x (średnia próbki) |
| Proporcja | π (proporcja populacji) | p (proporcja próbki) |
Chcemy obliczyć parametry populacji, ale ponieważ trwa to zbyt długo i kosztuje zbyt wiele, zamiast tego do obliczenia szacunków punktowych używamy próbek.
Załóżmy na przykład, że chcemy oszacować średnią wagę określonego gatunku żółwia na Florydzie. Ponieważ na Florydzie żyją tysiące żółwi, obchodzenie i ważenie każdego żółwia z osobna byłoby niezwykle czasochłonne i kosztowne. Zamiast tego moglibyśmy pobrać prostą losową próbkę 50 żółwi i użyć średniej masy żółwi w tej próbie do oszacowania prawdziwej średniej populacji:

Jeśli średnia próbki wynosi 150,4 funta, wówczas nasze oszacowanie punktowe prawdziwej średniej populacji całego gatunku wyniesie 150,4 funta.
Znaczenie próbek reprezentatywnych
Kiedy zbieramy próbkę z populacji, w idealnym przypadku chcielibyśmy, aby próbka przypominała „miniwersję” naszej populacji.
Próbkę uznaje się za reprezentatywną dla populacji , jeżeli cechy osób w próbie ściśle odpowiadają cechom osób w całej populacji.
Kiedy tak się stanie, możemy z całą pewnością uogólnić wyniki z próby na całą populację i możemy powiedzieć, że estymacja punktu próbkowania jest bezstronnym oszacowaniem prawdziwego parametru populacji.
Oszacowania punktowe i przedziały ufności
Chociaż estymacja punktowa reprezentuje nasze najlepsze możliwe oszacowanie prawdziwego parametru populacji, jest mało prawdopodobne, aby dokładnie odpowiadała parametrowi populacji.
W naszym poprzednim przykładzie nie ma gwarancji, że średnia waga żółwi w próbie dokładnie odpowiada średniej masie żółwi w całej populacji. Na przykład możemy wybrać próbkę pełną żółwi o małej wadze lub próbkę pełną żółwi ciężkich.
Aby więc uchwycić tę niepewność, możemy utworzyć przedział ufności – zakres wartości, który prawdopodobnie będzie zawierał parametr populacji z pewnym poziomem ufności.
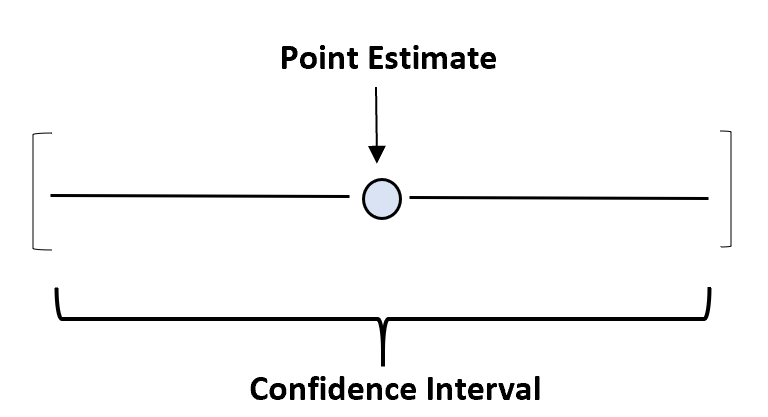
Na przykład możemy użyć naszej średniej próbki wynoszącej 150,4 funta, aby oszacować rzeczywistą średnią wagę gatunku żółwia. Nasz przedział ufności byłby wówczas zakresem wartości – być może od 145 funtów do 155,8 funtów.
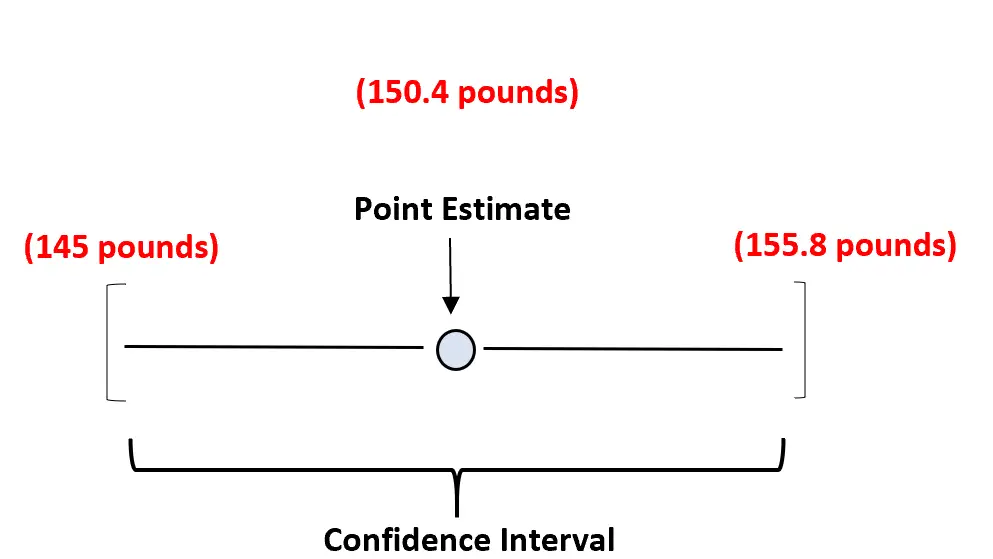
Nasze oszacowanie punktowe jest naszym najlepszym oszacowaniem prawdziwej średniej masy populacji, a przedział ufności zapewnia zakres wartości, które prawdopodobnie zawierają prawdziwą średnią masę populacji.
Więcej informacji na temat przedziałów ufności można znaleźć tutaj .
Dodatkowe zasoby
Statystyki vs. parametry: jaka jest różnica?
Populacja vs. próbka: jaka jest różnica?
Wprowadzenie do przedziałów ufności