Jak wykonać regresję kwadratową w pythonie

Regresja kwadratowa to rodzaj regresji, którego możemy użyć do ilościowego określenia związku między zmienną predykcyjną a zmienną odpowiedzi, gdy prawdziwe relacje są kwadratowe, co może wyglądać jak „U” lub odwrócone „U” na wykresie.

Oznacza to, że wraz ze wzrostem zmiennej predykcyjnej zmienna odpowiedzi również ma tendencję do wzrostu, ale po pewnym momencie zmienna odpowiedzi zaczyna się zmniejszać w miarę dalszego wzrostu zmiennej predykcyjnej.

W tym samouczku wyjaśniono, jak przeprowadzić regresję kwadratową w języku Python.

Przykład: regresja kwadratowa w Pythonie

Załóżmy, że mamy dane dotyczące liczby godzin przepracowanych tygodniowo i zgłoszonego poziomu szczęścia (w skali od 0 do 100) dla 16 różnych osób:

 import numpy as np
import scipy.stats as stats

#define variables
hours = [6, 9, 12, 12, 15, 21, 24, 24, 27, 30, 36, 39, 45, 48, 57, 60]
happ = [12, 18, 30, 42, 48, 78, 90, 96, 96, 90, 84, 78, 66, 54, 36, 24]

Jeśli stworzymy prosty wykres punktowy tych danych, zobaczymy, że związek między dwiema zmiennymi ma kształt litery „U”:

 import matplotlib.pyplot as plt

#create scatterplot
plt.scatter(hours, happ) 

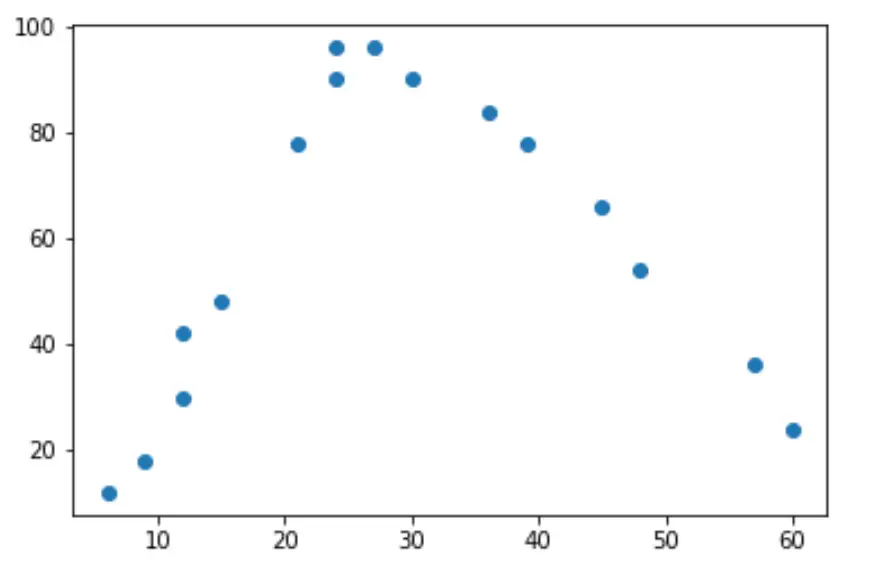
Wraz ze wzrostem liczby przepracowanych godzin wzrasta również szczęście, ale gdy przepracowane godziny przekraczają około 35 godzin tygodniowo, szczęście zaczyna spadać.

Ze względu na kształt litery „U” oznacza to, że regresja kwadratowa jest prawdopodobnie dobrym kandydatem do ilościowego określenia związku między dwiema zmiennymi.

Aby faktycznie przeprowadzić regresję kwadratową, możemy dopasować model regresji wielomianowej o stopniu 2 za pomocą funkcji numpy.polyfit() :

 import numpy as np

#polynomial fit with degree = 2
model = np.poly1d(np.polyfit(hours, happ, 2))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 60, 50)
plt.scatter(hours, happ)
plt.plot(polyline, model(polyline))
plt.show() 

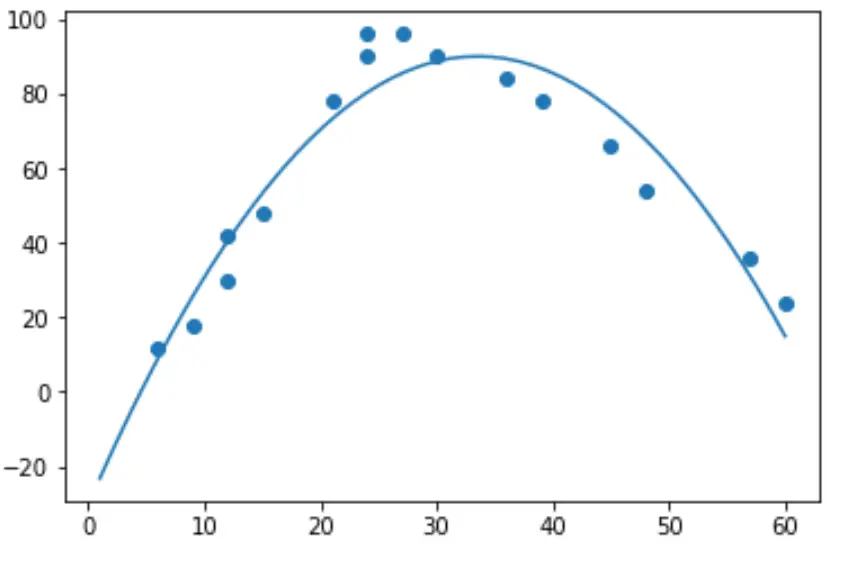
Dopasowane równanie regresji wielomianowej możemy otrzymać drukując współczynniki modelu:

 print (model)

-0.107x 2 + 7.173x - 30.25

Dopasowane równanie regresji kwadratowej to:

Szczęście = -0,107(godziny) ² + 7,173(godziny) – 30,25

Możemy użyć tego równania do obliczenia oczekiwanego poziomu szczęścia danej osoby na podstawie przepracowanych godzin. Przykładowo oczekiwany poziom szczęścia osoby pracującej 30 godzin tygodniowo wynosi:

Szczęście = -0,107(30) ² + 7,173(30) – 30,25 = 88,64 .

Możemy również napisać krótką funkcję, aby uzyskać R-kwadrat modelu, który jest proporcją wariancji zmiennej odpowiedzi, którą można wyjaśnić za pomocą zmiennych predykcyjnych.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np.polyfit(x, y, degree)
    p = np.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np.sum(y)/len(y)
    ssreg = np.sum((yhat-ybar)**2)
    sstot = np.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(hours, happ, 2)

{'r_squared': 0.9092114182131691}

W tym przykładzie kwadrat R modelu wynosi 0,9092 .

Oznacza to, że 90,92% zmienności zgłaszanych poziomów szczęścia można wyjaśnić zmiennymi predykcyjnymi.

Dodatkowe zasoby

Jak wykonać regresję wielomianową w Pythonie
Jak wykonać regresję kwadratową w R
Jak wykonać regresję kwadratową w programie Excel