Jak wykonać regresję sześcienną w pythonie

Regresja sześcienna to rodzaj regresji, którego możemy użyć do ilościowego określenia związku między zmienną predykcyjną a zmienną odpowiedzi, gdy związek między zmiennymi jest nieliniowy.

W tym samouczku wyjaśniono, jak przeprowadzić regresję sześcienną w języku Python.

Przykład: regresja sześcienna w Pythonie

Załóżmy, że mamy następującą ramkę danych pandy, która zawiera dwie zmienne (x i y):

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' x ': [6, 9, 12, 16, 22, 28, 33, 40, 47, 51, 55, 60],
                   ' y ': [14, 28, 50, 64, 67, 57, 55, 57, 68, 74, 88, 110]})

#view DataFrame
print (df)

     xy
0 6 14
1 9 28
2 12 50
3 16 64
4 22 67
5 28 57
6 33 55
7 40 57
8 47 68
9 51 74
10 55 88
11 60 110

Jeśli zrobimy prosty wykres rozrzutu tych danych, zobaczymy, że związek między dwiema zmiennymi jest nieliniowy:

 import matplotlib. pyplot as plt

#create scatterplot
plt. scatter (df. x , df. y ) 

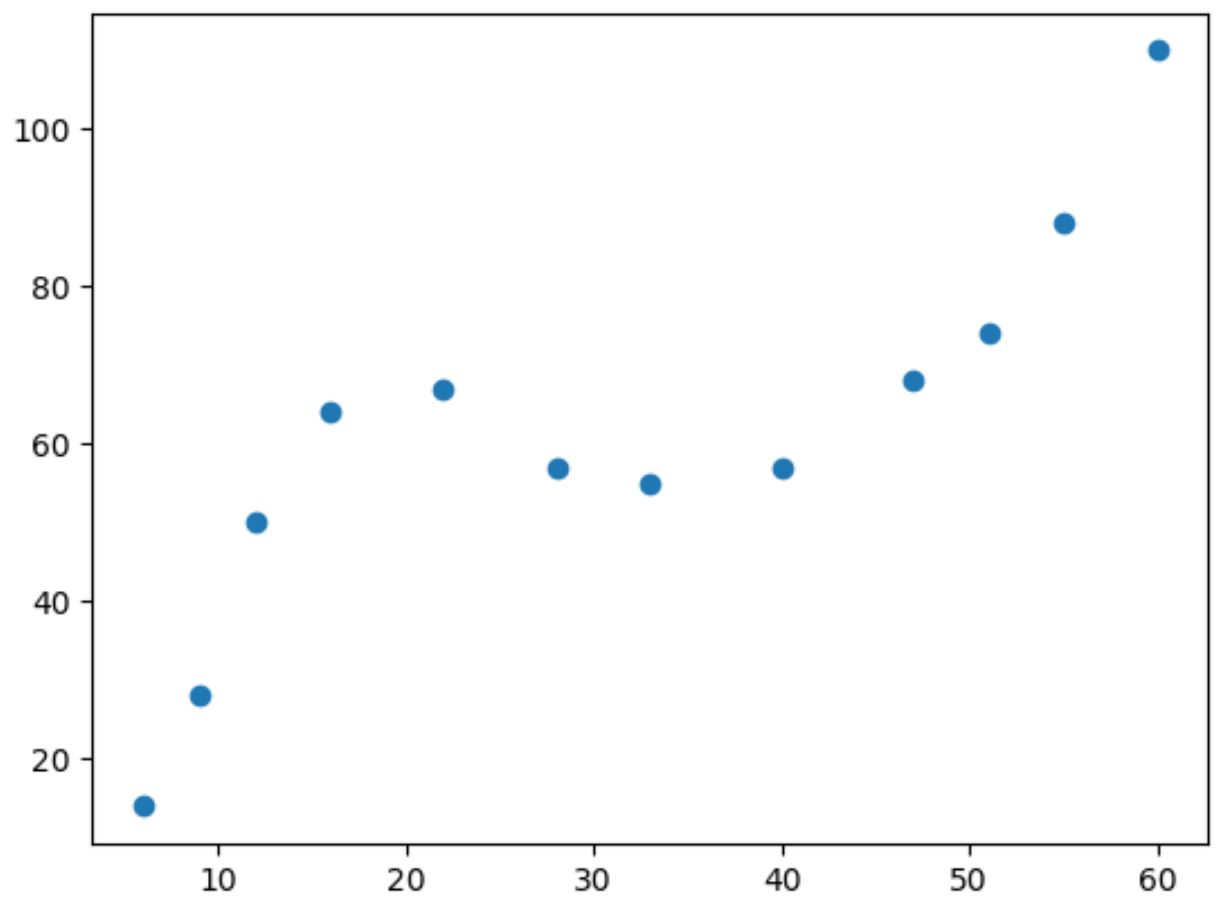
Wraz ze wzrostem wartości x y wzrasta do pewnego punktu, następnie maleje i ponownie rośnie.

Ten wzór z dwiema „krzywymi” na wykresie wskazuje na sześcienną zależność między dwiema zmiennymi.

Oznacza to, że model regresji sześciennej jest dobrym kandydatem do ilościowego określenia związku między dwiema zmiennymi.

Aby wykonać regresję sześcienną, możemy dopasować model regresji wielomianowej stopnia 3 za pomocą funkcji numpy.polyfit() :

 import numpy as np

#fit cubic regression model
model = np. poly1d (np. polyfit (df. x , df. y , 3))

#add fitted cubic regression line to scatterplot
polyline = np. linspace (1, 60, 50)
plt. scatter (df. x , df. y )
plt. plot (polyline, model(polyline))

#add axis labels
plt. xlabel (' x ')
plt. ylabel (' y ')

#displayplot
plt. show () 

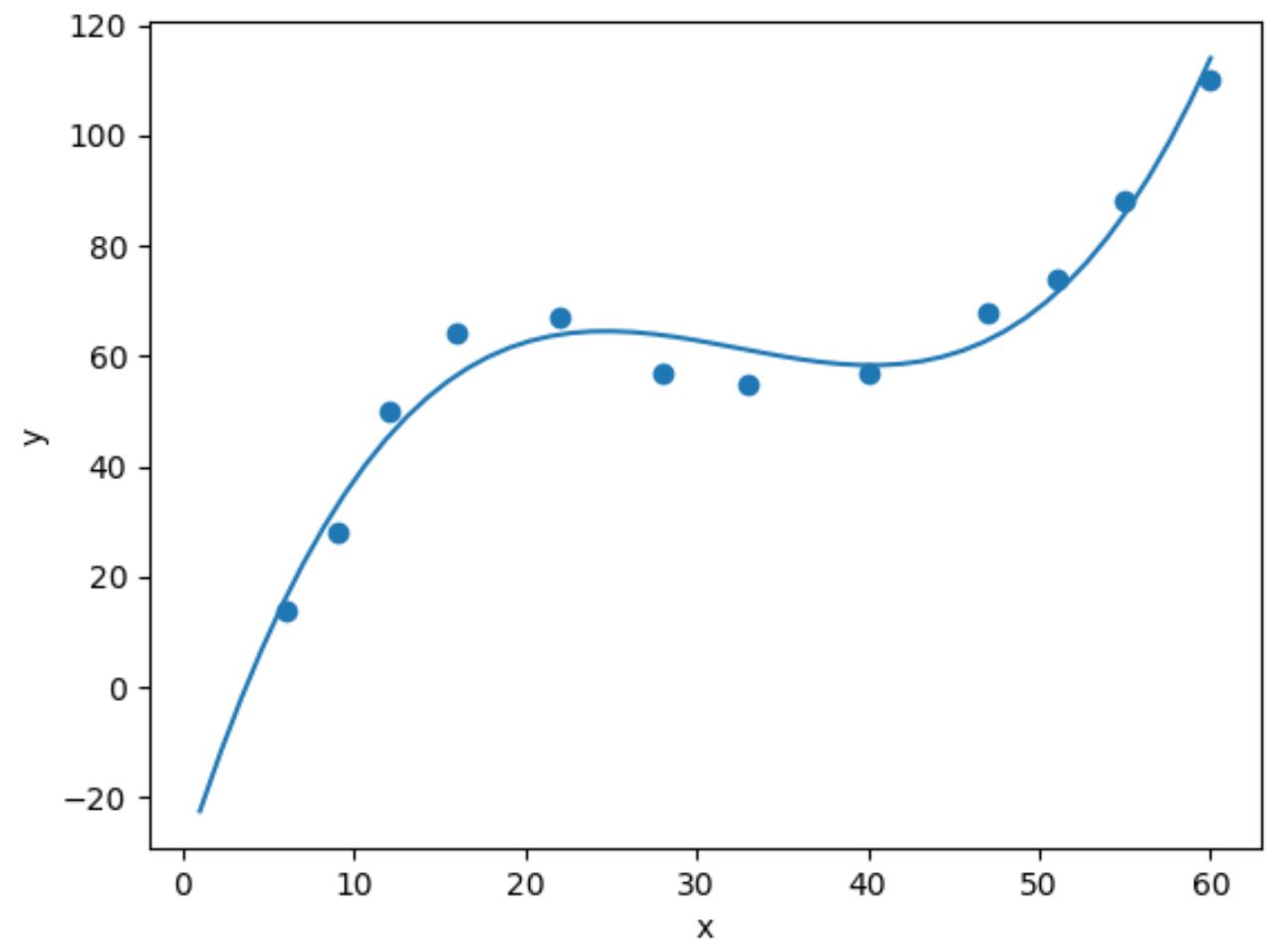
Dopasowane równanie regresji sześciennej możemy otrzymać drukując współczynniki modelu:

 print (model)

          3 2
0.003302x - 0.3214x + 9.832x - 32.01

Dopasowane równanie regresji sześciennej to:

y = 0,003302(x) ³ – 0,3214(x) ² + 9,832x – 30,01

Możemy użyć tego równania do obliczenia oczekiwanej wartości y na podstawie wartości x.

Na przykład, jeśli x wynosi 30, wówczas oczekiwana wartość y wynosi 64,844:

y = 0,003302(30) ³ – 0,3214(30) ² + 9,832(30) – 30,01 = 64,844

Możemy również napisać krótką funkcję, aby uzyskać R-kwadrat modelu, który jest proporcją wariancji zmiennej odpowiedzi, którą można wyjaśnić za pomocą zmiennych predykcyjnych.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar) ** 2)
    sstot = np. sum ((y - ybar) ** 2)
    results[' r_squared '] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(df. x , df. y , 3)

{'r_squared': 0.9632469890057967}

W tym przykładzie kwadrat R modelu wynosi 0,9632 .

Oznacza to, że 96,32% zmienności zmiennej odpowiedzi można wyjaśnić zmienną predykcyjną.

Ponieważ wartość ta jest tak wysoka, mówi nam to, że model regresji sześciennej dobrze określa ilościowo związek między dwiema zmiennymi.

Powiązane: Jaka jest dobra wartość R-kwadrat?

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w Pythonie:

Jak wykonać prostą regresję liniową w Pythonie
Jak wykonać regresję kwadratową w Pythonie
Jak wykonać regresję wielomianową w Pythonie