Jak wykonać regresję wielomianową w pythonie

Analizę regresji stosuje się do ilościowego określenia związku między jedną lub większą liczbą zmiennych objaśniających a zmienną odpowiedzi.

Najpopularniejszym rodzajem analizy regresji jest prosta regresja liniowa , stosowana, gdy zmienna predykcyjna i zmienna odpowiedzi mają liniową zależność.

Czasami jednak związek między zmienną predykcyjną a zmienną odpowiedzi jest nieliniowy.

Na przykład prawdziwa zależność może być kwadratowa:

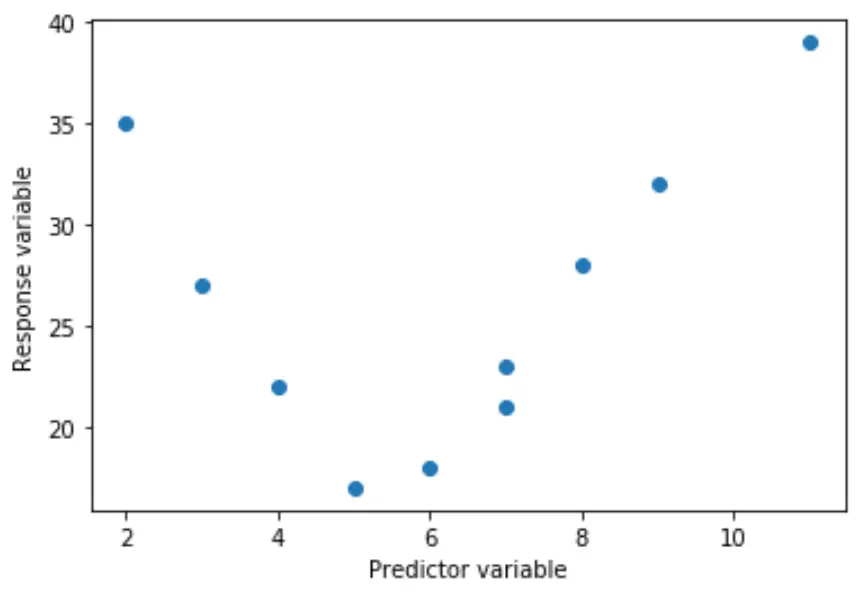
Lub może być sześcienny:

W takich przypadkach sensowne jest zastosowanie regresji wielomianowej , która może wyjaśnić nieliniową zależność między zmiennymi.

W tym samouczku wyjaśniono, jak przeprowadzić regresję wielomianową w języku Python.

Przykład: regresja wielomianowa w Pythonie

Załóżmy, że w Pythonie mamy następującą zmienną predykcyjną (x) i zmienną odpowiedzi (y):

 x = [2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12]
y = [18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29]

Jeśli utworzymy prosty wykres rozrzutu tych danych, zobaczymy, że związek między x i y wyraźnie nie jest liniowy:

 import matplotlib.pyplot as plt

#create scatterplot 
plt.scatter(x, y)

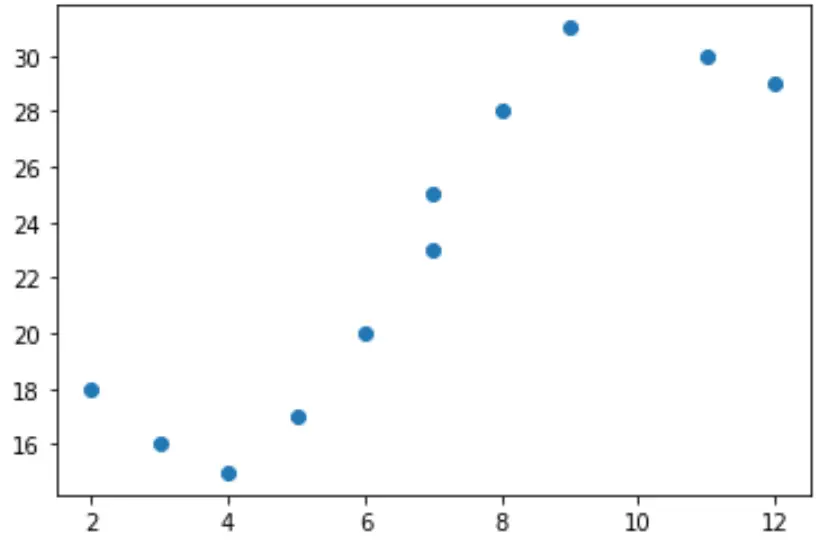
Dopasowanie modelu regresji liniowej do tych danych nie miałoby zatem sensu. Zamiast tego możemy spróbować dopasować model regresji wielomianowej o stopniu 3 za pomocą funkcji numpy.polyfit() :

 import numpy as np

#polynomial fit with degree = 3
model = np.poly1d(np.polyfit(x, y, 3))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 12, 50)
plt.scatter(x, y)
plt.plot(polyline, model(polyline))
plt.show() 

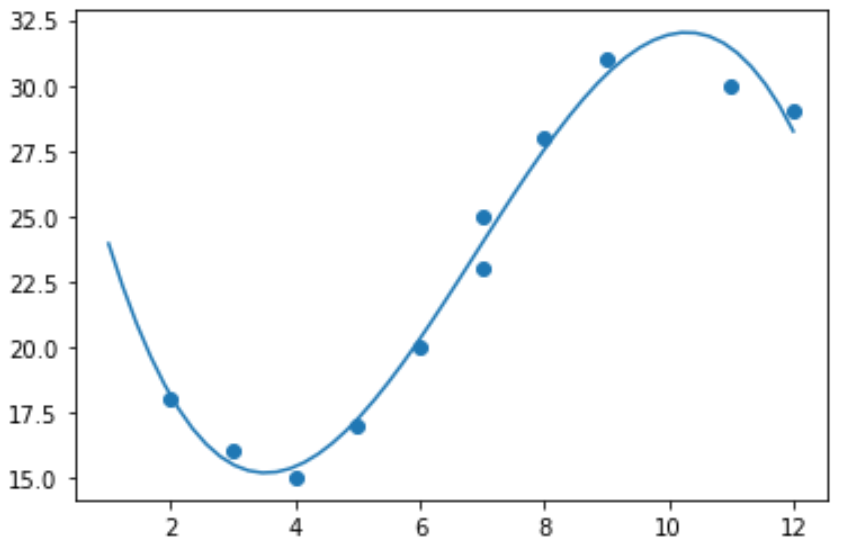
Dopasowane równanie regresji wielomianowej możemy otrzymać drukując współczynniki modelu:

 print(model)

poly1d([ -0.10889554, 2.25592957, -11.83877127, 33.62640038])

Dopasowane równanie regresji wielomianowej to:

y = -0,109x ³ + 2,256x ² – 11,839x + 33,626

Równanie to można wykorzystać do znalezienia oczekiwanej wartości zmiennej odpowiedzi przy danej wartości zmiennej objaśniającej.

Załóżmy na przykład, że x = 4. Oczekiwana wartość zmiennej odpowiedzi y będzie wynosić:

y = -0,109(4) ³ + 2,256(4) ² – 11,839(4) + 33,626= 15,39 .

Możemy również napisać krótką funkcję, aby uzyskać R-kwadrat modelu, który jest proporcją wariancji zmiennej odpowiedzi, którą można wyjaśnić za pomocą zmiennych predykcyjnych.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = numpy.polyfit(x, y, degree)
    p = numpy.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = numpy.sum(y)/len(y)
    ssreg = numpy.sum((yhat-ybar)**2)
    sstot = numpy.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(x, y, 3)

{'r_squared': 0.9841113454245183}

W tym przykładzie kwadrat R modelu wynosi 0,9841 .

Oznacza to, że 98,41% zmienności zmiennej odpowiedzi można wyjaśnić zmiennymi predykcyjnymi.