Jak wykonać transformację boxa-coxa w pythonie

Transformacja Boxa-Coxa jest powszechnie stosowaną metodą przekształcania zbioru danych o rozkładzie normalnym w zbiór o bardziej normalnym rozkładzie.

Podstawową ideą tej metody jest znalezienie takiej wartości λ, aby przekształcone dane były jak najbardziej zbliżone do rozkładu normalnego, korzystając ze wzoru:

• y(λ) = (y ^λ – 1) / λ jeśli y ≠ 0
• y(λ) = log(y), jeśli y = 0

Transformację box-cox możemy wykonać w Pythonie za pomocą funkcji scipy.stats.boxcox() .

Poniższy przykład pokazuje, jak w praktyce wykorzystać tę funkcję.

Przykład: transformacja Boxa-Coxa w Pythonie

Załóżmy, że generujemy losowy zbiór 1000 wartości z rozkładu wykładniczego :

 #load necessary packages
import numpy as np 
from scipy. stats import boxcox 
import seaborn as sns 

#make this example reproducible
n.p. random . seeds (0)

#generate dataset
data = np. random . exponential (size= 1000 )

#plot the distribution of data values
sns. distplot (data, hist= False , kde= True ) 

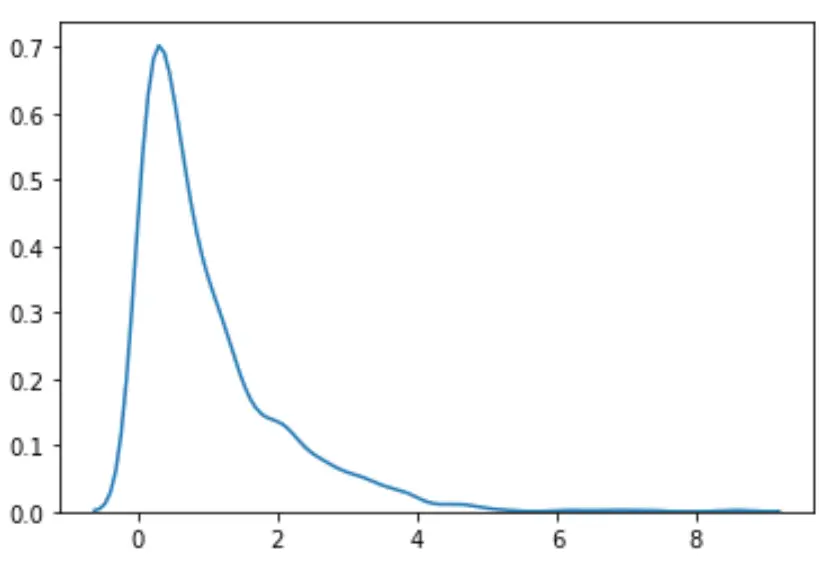
Widzimy, że rozkład nie wydaje się normalny.

Możemy użyć funkcji boxcox() , aby znaleźć optymalną wartość lambda, która daje bardziej normalny rozkład:

 #perform Box-Cox transformation on original data
transformed_data, best_lambda = boxcox(data) 

#plot the distribution of the transformed data values
sns. distplot (transformed_data, hist= False , kde= True ) 

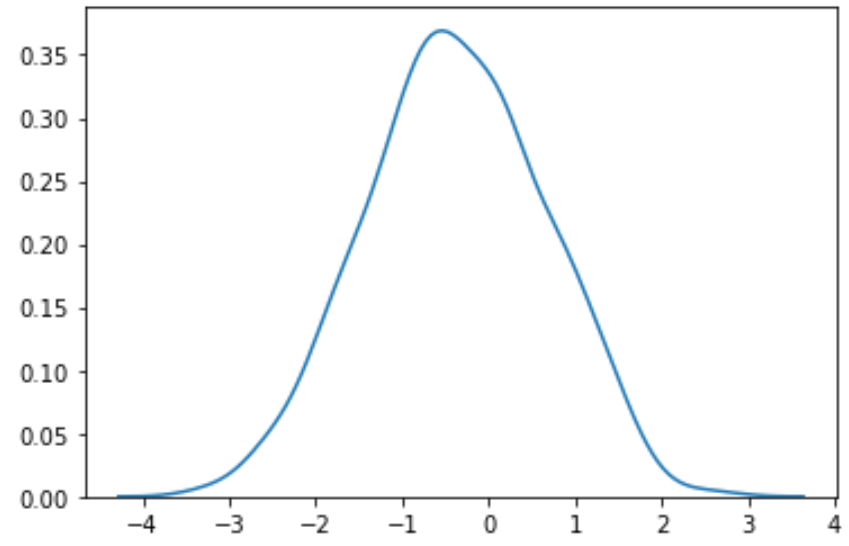
Widzimy, że przekształcone dane mają znacznie bardziej normalny rozkład.

Możemy również znaleźć dokładną wartość lambda użytą do wykonania transformacji Boxa-Coxa:

 #display optimal lambda value
print (best_lambda)

0.2420131978174143

Stwierdzono, że optymalna lambda wynosi około 0,242 .

Zatem każdą wartość danych przekształcono przy użyciu następującego równania:

Nowy = (stary ^0,242 – 1) / 0,242

Możemy to potwierdzić, patrząc na wartości danych oryginalnych w porównaniu z danymi przekształconymi:

 #view first five values of original dataset
data[0:5]

array([0.79587451, 1.25593076, 0.92322315, 0.78720115, 0.55104849])

#view first five values of transformed dataset
transformed_data[0:5]

array([-0.22212062, 0.23427768, -0.07911706, -0.23247555, -0.55495228])

Pierwsza wartość w oryginalnym zbiorze danych wynosiła 0,79587 . Zastosowaliśmy więc następujący wzór do przekształcenia tej wartości:

Nowy = (0,79587 ^0,242 – 1) / 0,242 = -0,222

Możemy potwierdzić, że pierwsza wartość w przekształconym zbiorze danych rzeczywiście wynosi -0,222 .

Dodatkowe zasoby

Jak utworzyć i zinterpretować wykres QQ w Pythonie
Jak wykonać test normalności Shapiro-Wilka w Pythonie