Jak korzystać z rozkładu dwumianowego w pythonie

Rozkład dwumianowy jest jednym z najczęściej stosowanych rozkładów w statystyce. Opisuje prawdopodobieństwo uzyskania k sukcesów w n eksperymentach dwumianowych.

Jeśli zmienna losowa X ma rozkład dwumianowy, prawdopodobieństwo, że X = k powodzenia można obliczyć za pomocą następującego wzoru:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Złoto:

• n: liczba prób
• k: liczba sukcesów
• p: prawdopodobieństwo sukcesu w danej próbie
• _n C _k : liczba sposobów uzyskania k sukcesów w n próbach

W tym samouczku wyjaśniono, jak używać rozkładu dwumianowego w Pythonie.

Jak wygenerować rozkład dwumianowy

Możesz wygenerować tablicę wartości, która ma rozkład dwumianowy, korzystając z funkcji random.binomial biblioteki numpy:

 from numpy import random

#generate an array of 10 values that follows a binomial distribution
random.binomial(n=10, p=.25, size=10)

array([5, 2, 1, 3, 3, 3, 2, 2, 1, 4])

Każda liczba w wynikowej tabeli reprezentuje liczbę „sukcesów” odniesionych w ciągu 10 prób, gdzie prawdopodobieństwo sukcesu w danej próbie wynosiło 0,25 .

Jak obliczyć prawdopodobieństwa za pomocą rozkładu dwumianowego

Możesz także odpowiedzieć na pytania dotyczące prawdopodobieństwa dwumianu, korzystając z funkcji binom biblioteki scipy.

Pytanie 1: Nathan wykonuje 60% swoich prób rzutów wolnych. Jeśli wykona 12 rzutów wolnych, jakie jest prawdopodobieństwo, że trafi dokładnie 10?

 from scipy.stats import binom

#calculate binomial probability
binom.pmf(k= 10 , n= 12 , p= 0.6 )

0.0639

Prawdopodobieństwo, że Nathan wykona dokładnie 10 rzutów wolnych, wynosi 0,0639 .

Pytanie 2: Marty rzuca 5 razy uczciwą monetą. Jakie jest prawdopodobieństwo, że na monecie wypadnie reszka 2 lub mniej?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 2 , n= 5 , p= 0.5 )

0.5

Prawdopodobieństwo, że na monecie wypadnie reszka 2 lub mniej, wynosi 0,5 .

Pytanie 3: Wiemy, że 70% osób popiera określone prawo. Jeśli losowo wybranych zostanie 10 osób, jakie jest prawdopodobieństwo, że od 4 do 6 z nich poprze prawo?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 6 , n= 10 , p= 0.7 ) - binom.cdf(k= 3 , n= 10 , p= 0.7 )

0.3398

Prawdopodobieństwo, że od 4 do 6 losowo wybranych osób popiera to prawo, wynosi 0,3398 .

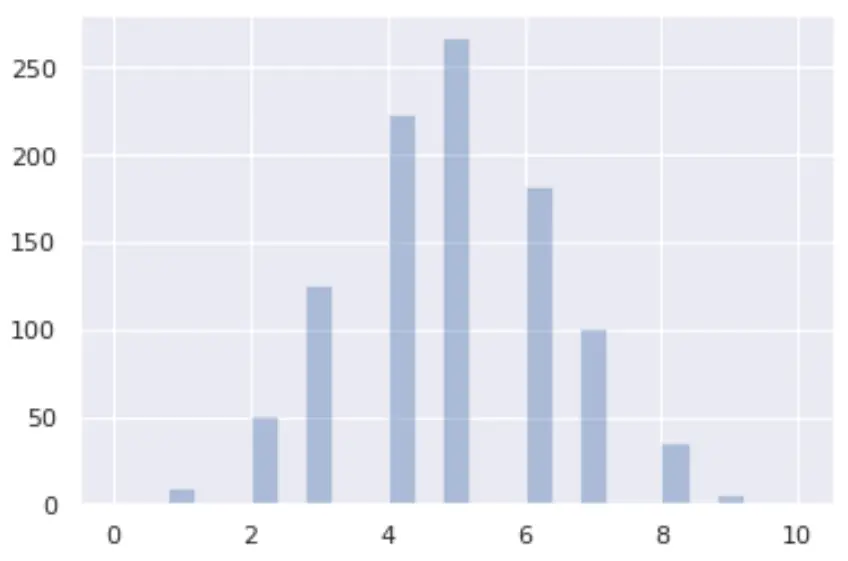
Jak wizualizować rozkład dwumianowy

Możesz wizualizować rozkład dwumianowy w Pythonie, korzystając z bibliotek seaborn i matplotlib :

 from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

x = random.binomial(n= 10 , p= 0.5 , size= 1000 )

sns.distplot(x, hist= True , kde= False )

plt.show()

Herbata