Jak narysować krzywą roc w pythonie (krok po kroku)

Regresja logistyczna to metoda statystyczna, której używamy do dopasowania modelu regresji, gdy zmienna odpowiedzi jest binarna. Aby ocenić, jak dobrze model regresji logistycznej pasuje do zbioru danych, możemy przyjrzeć się następującym dwóm metrykom:

• Czułość: prawdopodobieństwo, że model przewiduje pozytywny wynik obserwacji, gdy wynik jest rzeczywiście pozytywny. Nazywa się to również „prawdziwie dodatnią stopą procentową”.
• Specyficzność: prawdopodobieństwo, że model przewiduje negatywny wynik obserwacji, gdy wynik jest faktycznie negatywny. Nazywa się to również „prawdziwie ujemną stopą”.

Jednym ze sposobów wizualizacji tych dwóch pomiarów jest utworzenie krzywej ROC , która oznacza krzywą „charakterystyki działania odbiornika”. To jest wykres przedstawiający czułość i swoistość modelu regresji logistycznej.

Poniższy przykład krok po kroku pokazuje, jak utworzyć i zinterpretować krzywą ROC w Pythonie.

Krok 1: Zaimportuj niezbędne pakiety

Najpierw zaimportujemy niezbędne pakiety, aby wykonać regresję logistyczną w Pythonie:

 import pandas as pd
import numpy as np
from sklearn. model_selection import train_test_split
from sklearn. linear_model import LogisticRegression
from sklearn import metrics
import matplotlib. pyplot as plt

Krok 2: Dopasuj model regresji logistycznej

Następnie zaimportujemy zbiór danych i dopasujemy do niego model regresji logistycznej:

 #import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv"
data = pd. read_csv (url)

#define the predictor variables and the response variable
X = data[[' student ',' balance ',' income ']]
y = data[' default ']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0) 

#instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression. fit (X_train,y_train)

Krok 3: Narysuj krzywą ROC

Następnie obliczymy współczynnik prawdziwie dodatni i współczynnik fałszywie dodatni i utworzymy krzywą ROC za pomocą pakietu wizualizacji danych Matplotlib:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr)
plt. ylabel (' True Positive Rate ')
plt. xlabel (' False Positive Rate ')
plt. show () 

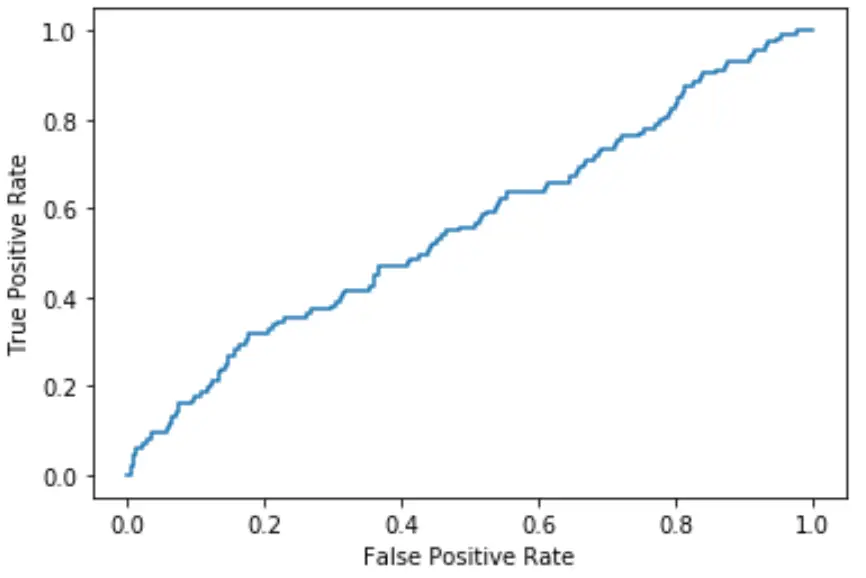
Im bardziej krzywa pasuje do lewego górnego rogu wykresu, tym lepiej model jest w stanie sklasyfikować dane w kategorie.

Jak widać na powyższym wykresie, ten model regresji logistycznej dość słabo radzi sobie z sortowaniem danych na kategorie.

Aby to określić ilościowo, możemy obliczyć AUC – obszar pod krzywą – który mówi nam, jaka część wykresu znajduje się pod krzywą.

Im AUC jest bliższe 1, tym lepszy model. Model z AUC równym 0,5 nie jest lepszy od modelu przeprowadzającego losową klasyfikację.

Krok 4: Oblicz AUC

Możemy użyć poniższego kodu do obliczenia AUC modelu i wyświetlenia go w prawym dolnym rogu wykresu ROC:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. ylabel (' True Positive Rate ')
plt. xlabel (' False Positive Rate ')
plt. legend (loc=4)
plt. show () 

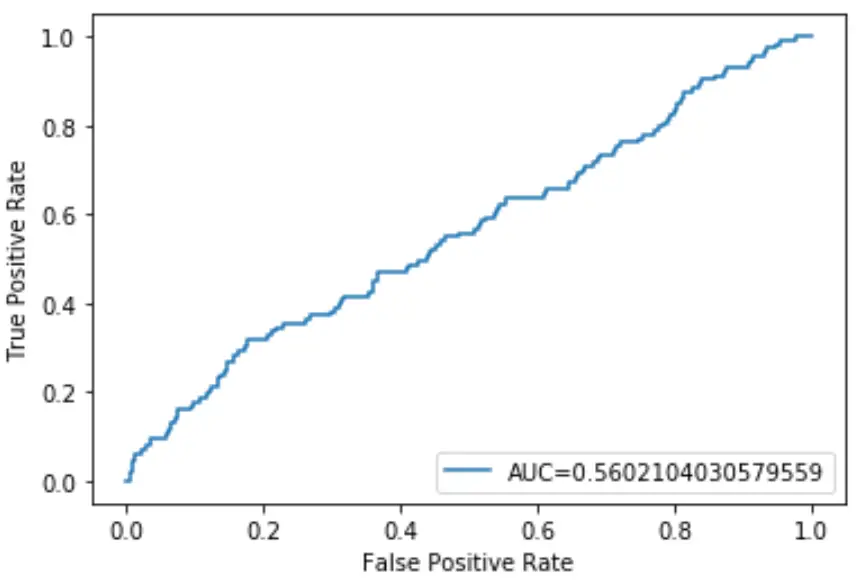
Okazuje się, że AUC tego modelu regresji logistycznej wynosi 0,5602 . Ponieważ liczba ta jest zamknięta do 0,5, potwierdza to, że model słabo radzi sobie z klasyfikacją danych.

Powiązane: Jak wykreślić wiele krzywych ROC w Pythonie