Jak korzystać z rozkładu poissona w pythonie

Rozkład Poissona opisuje prawdopodobieństwo uzyskania k sukcesów w zadanym przedziale czasu.

Jeśli zmienna losowa X ma rozkład Poissona, prawdopodobieństwo, że X = k powodzenia można obliczyć za pomocą następującego wzoru:

P(X=k) = λ ^k * e ^{– λ} / k!

Złoto:

• λ: średnia liczba sukcesów występujących w określonym przedziale czasu
• k: liczba sukcesów
• e: stała równa około 2,71828

W tym samouczku wyjaśniono, jak używać rozkładu Poissona w języku Python.

Jak wygenerować rozkład Poissona

Możesz użyć funkcji Poisson.rvs(mu, size) do wygenerowania losowych wartości z rozkładu Poissona o określonej wartości średniej i wielkości próbki:

 from scipy. stats import fish

#generate random values from Poisson distribution with mean=3 and sample size=10
fish. rvs (mu=3, size=10)

array([2, 2, 2, 0, 7, 2, 1, 2, 5, 5])

Jak obliczyć prawdopodobieństwa za pomocą rozkładu Poissona

Za pomocą funkcji Poisson.pmf(k, mu) i Poisson.cdf(k, mu) można obliczyć prawdopodobieństwa związane z rozkładem Poissona.

Przykład 1: Prawdopodobieństwo równe określonej wartości

Sklep sprzedaje średnio 3 jabłka dziennie. Jakie jest prawdopodobieństwo, że danego dnia sprzedają 5 jabłek?

 from scipy. stats import fish

#calculate probability
fish. pmf (k=5, mu=3)

0.100819

Prawdopodobieństwo, że w danym dniu sklep sprzeda 5 jabłek wynosi 0,100819 .

Przykład 2: Prawdopodobieństwo mniejsze niż pewna wartość

W pewnym sklepie sprzedaje się średnio siedem piłek dziennie. Jakie jest prawdopodobieństwo, że w danym dniu ten sklep sprzeda cztery lub mniej piłek?

 from scipy. stats import fish

#calculate probability
fish. cdf (k=4, mu=7)

0.172992

Prawdopodobieństwo, że danego dnia sklep sprzeda cztery lub mniej piłek wynosi 0,172992 .

Przykład 3: Prawdopodobieństwo większe niż pewna wartość

W pewnym sklepie sprzedaje się średnio 15 puszek tuńczyka dziennie. Jakie jest prawdopodobieństwo, że w tym sklepie danego dnia sprzeda się więcej niż 20 puszek tuńczyka?

 from scipy. stats import fish

#calculate probability
1-fish. cdf (k=20, mu=15)

0.082971

Prawdopodobieństwo, że w danym dniu sklep sprzeda więcej niż 20 puszek tuńczyka, wynosi 0,082971 .

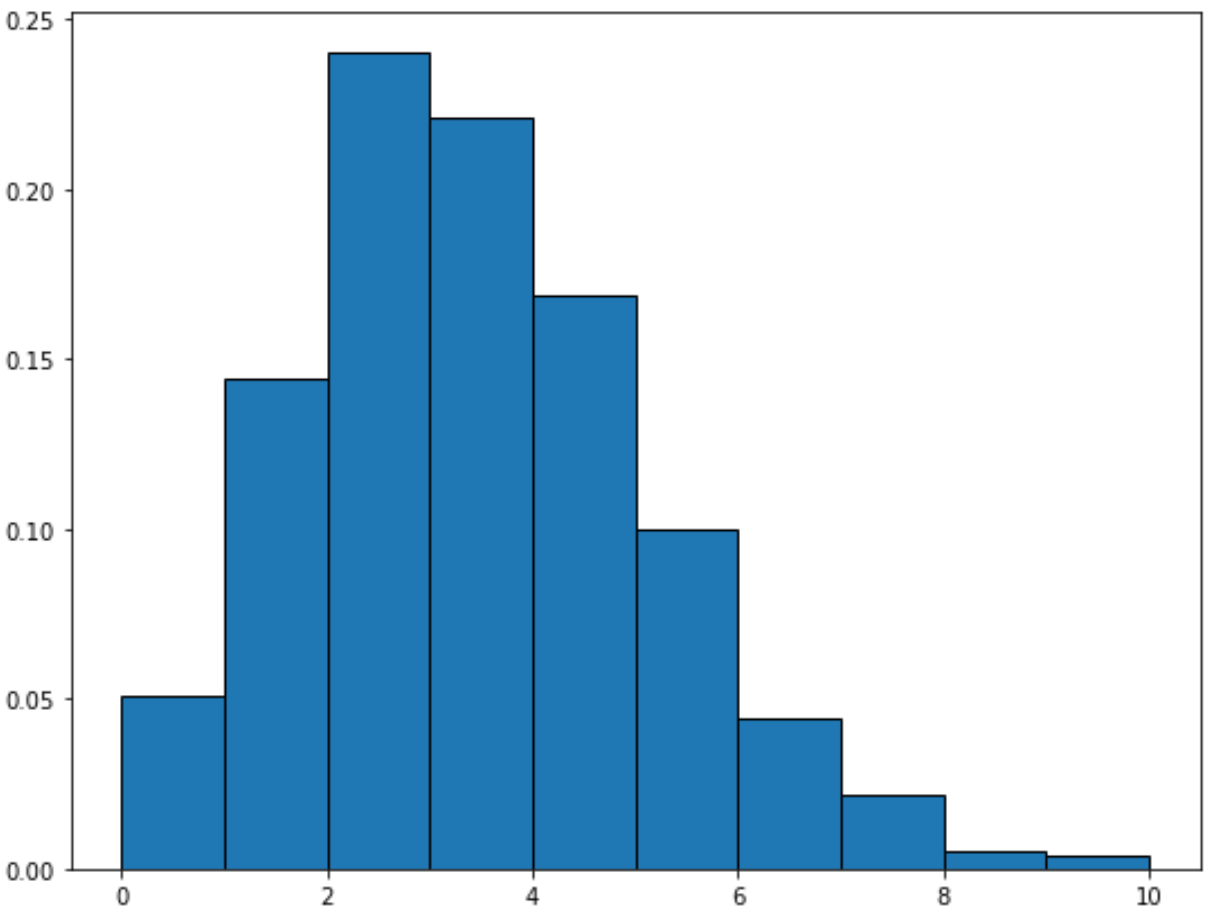
Jak wykreślić rozkład Poissona

Aby wykreślić rozkład Poissona z daną średnią, można zastosować następującą składnię:

 from scipy. stats import fish
import matplotlib. pyplot as plt

#generate Poisson distribution with sample size 10000
x = fish. rvs (mu=3, size=10000)

#create plot of Poisson distribution
plt. hist (x, density= True , edgecolor=' black ')

Dodatkowe zasoby

Wprowadzenie do rozkładu Poissona
5 konkretnych przykładów rozkładu Poissona
Kalkulator dystrybucji ryb online