Jak ręcznie wykonać sparowany test t

Test t dla par prób służy do porównania średnich z dwóch próbek, gdy każdą obserwację w jednej próbie można powiązać z obserwacją w drugiej próbie.

Poniższy przykład pokazuje krok po kroku, jak przeprowadzić test t dla par próbek, aby ustalić, czy średnie populacji są równe w następujących dwóch grupach:

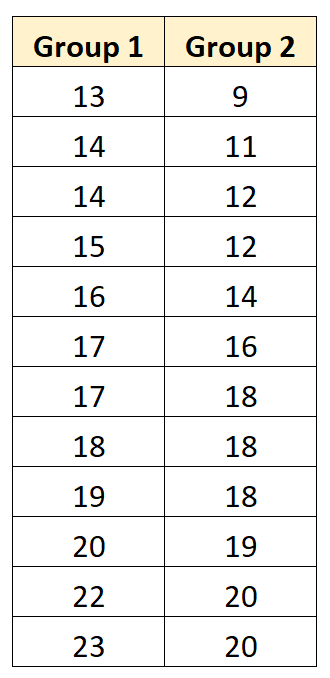
Krok 1: Oblicz statystykę testową

Statystykę testową sparowanego testu t oblicza się w następujący sposób:

t = x _różnica / (s _różnica /√ n )

Złoto:

• x _diff : przykład średniej różnic
• s: przykład odchylenia standardowego różnic
• n: wielkość próby (tj. liczba par)

Obliczymy średnią różnic między obiema grupami i odchylenie standardowe różnic między obiema grupami:

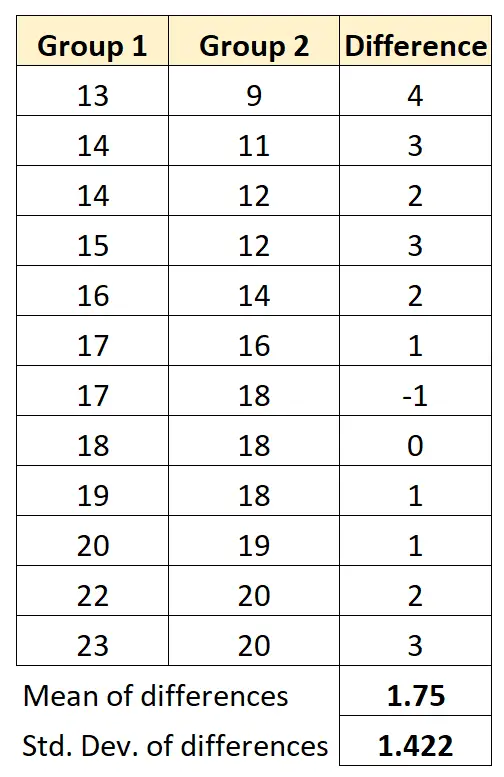
Zatem naszą statystykę testową można obliczyć w następujący sposób:

• t = x _różnica / (s _różnica /√ n )
• t = 1,75 / (1,422/√ 12 )
• t = 4,26

Krok 2: Oblicz wartość krytyczną

Następnie musimy znaleźć wartość krytyczną, z którą będziemy mogli porównać nasze statystyki testowe.

W tym przykładzie użyjemy testu dwustronnego z α = 0,05 i df = n-1 stopniami swobody.

Zgodnie z tabelą rozkładu t wartość krytyczna odpowiadająca tym wartościom wynosi 2,201 :

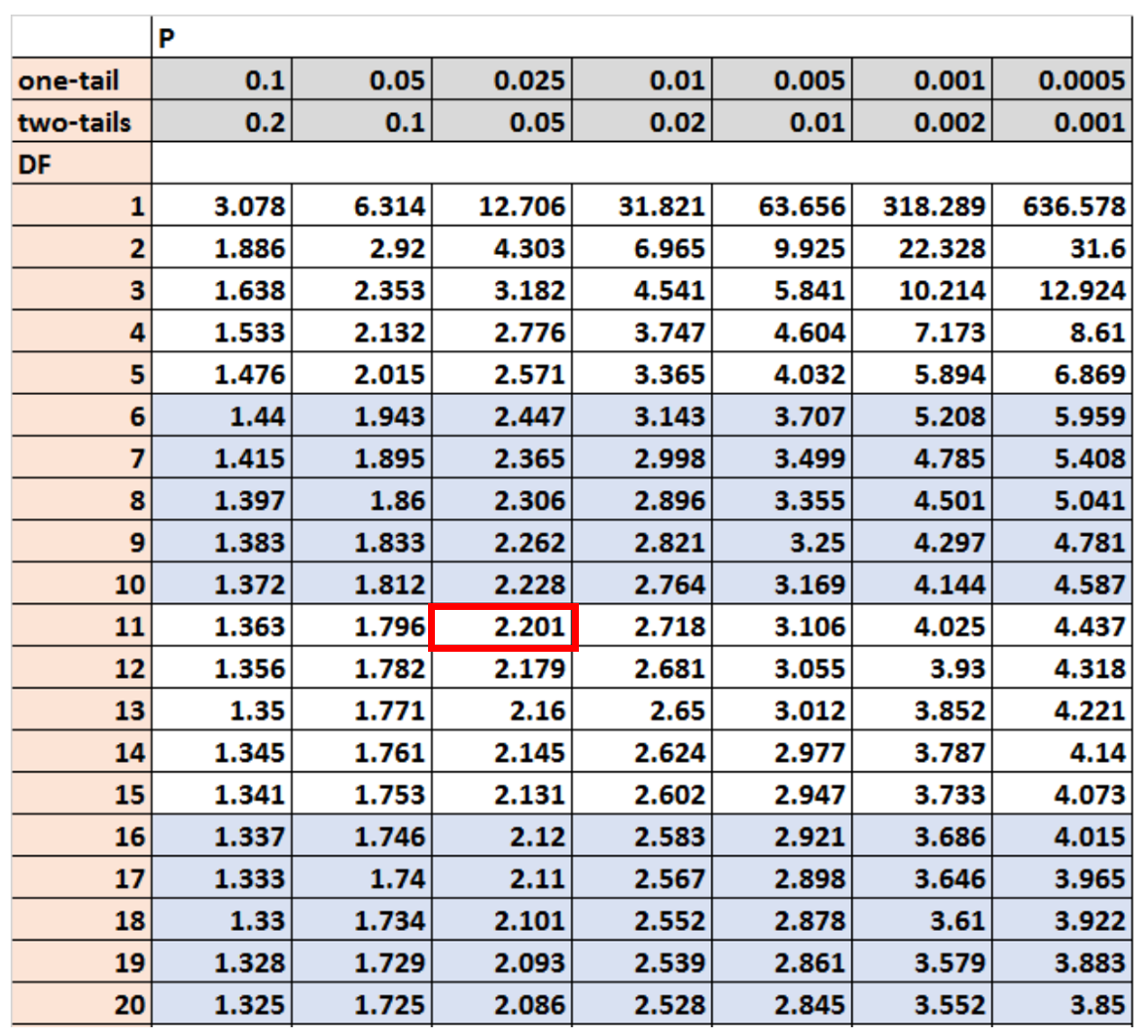
Krok 3: Odrzuć lub nie odrzuć hipotezę zerową

Nasz test t dla sparowanych próbek wykorzystuje następującą hipotezę zerową i alternatywną:

• H ₀ : μ ₁ = μ ₂ (średnie z obu populacji są równe)
• H _A : μ ₁ ≠ μ ₂ (średnie z obu populacji nie są równe)

Ponieważ wartość bezwzględna naszej statystyki testowej ( 4,26 ) jest większa niż wartość krytyczna znaleziona w tabeli t ( 2,201 ), odrzucamy hipotezę zerową.

Oznacza to, że mamy wystarczające dowody, aby stwierdzić, że średnia między obiema grupami nie jest równa.

Bonus: możesz skorzystać z kalkulatora testu t dla par próbek, aby potwierdzić swoje wyniki.