Regresja głównych komponentów w pythonie (krok po kroku)

Biorąc pod uwagę zbiór p zmiennych predykcyjnych i zmienną odpowiedzi, wielokrotna regresja liniowa wykorzystuje metodę znaną jako metoda najmniejszych kwadratów, aby zminimalizować resztową sumę kwadratów (RSS):

RSS = Σ(y _i – ŷ _i ) ²

Złoto:

• Σ : Grecki symbol oznaczający sumę
• y _i : rzeczywista wartość odpowiedzi dla ^i-tej obserwacji
• ŷ _i : Przewidywana wartość odpowiedzi na podstawie modelu wielokrotnej regresji liniowej

Jednakże, gdy zmienne predykcyjne są silnie skorelowane, współliniowość może stać się problemem. Może to sprawić, że szacunki współczynników modelu będą niewiarygodne i będą wykazywać dużą wariancję.

Jednym ze sposobów uniknięcia tego problemu jest zastosowanie regresji głównych składowych , która znajduje M kombinacji liniowych (zwanych „głównymi składowymi”) oryginalnych predyktorów p , a następnie wykorzystuje metodę najmniejszych kwadratów do dopasowania modelu regresji liniowej, wykorzystując główne składowe jako predyktory.

Ten samouczek zawiera przykład krok po kroku wykonywania regresji głównych składników w języku Python.

Krok 1: Zaimportuj niezbędne pakiety

Najpierw zaimportujemy pakiety potrzebne do przeprowadzenia regresji głównych składowych (PCR) w Pythonie:

 import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale 
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn.model_selection import train_test_split
from sklearn. PCA import decomposition
from sklearn. linear_model import LinearRegression
from sklearn. metrics import mean_squared_error

Krok 2: Załaduj dane

W tym przykładzie użyjemy zbioru danych o nazwie mtcars , który zawiera informacje o 33 różnych samochodach. Użyjemy hp jako zmiennej odpowiedzi i następujących zmiennych jako predyktorów:

• mpg
• wyświetlacz
• gówno
• waga
• sek

Poniższy kod pokazuje, jak załadować i wyświetlić ten zestaw danych:

 #define URL where data is located
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/mtcars.csv"

#read in data
data_full = pd. read_csv (url)

#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]

#view first six rows of data
data[0:6]


        mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105

Krok 3: Dostosuj model PCR

Poniższy kod pokazuje, jak dopasować model PCR do tych danych. Zwróć uwagę na następujące kwestie:

• pca.fit_transform(scale(X)) : Informuje Pythona, że każda zmienna predykcyjna powinna zostać przeskalowana tak, aby miała średnią 0 i odchylenie standardowe 1. Dzięki temu żadna zmienna predykcyjna nie będzie miała zbyt dużego wpływu na model, jeśli to się dzieje. mierzyć w różnych jednostkach.
• cv = RepeatedKFold() : Mówi Pythonowi, aby użył k-krotnej walidacji krzyżowej do oceny wydajności modelu. W tym przykładzie wybieramy k = 10 fałd, powtórzonych 3 razy.

 #define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]

#scale predictor variables
pca = pca()
X_reduced = pca. fit_transform ( scale (X))

#define cross validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )

regr = LinearRegression()
mse = []

# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (regr,
           n.p. ones ((len(X_reduced),1)), y, cv=cv,
           scoring=' neg_mean_squared_error '). mean ()    
mse. append (score)

# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
    score = -1*model_selection. cross_val_score (regr,
               X_reduced[:,:i], y, cv=cv, scoring=' neg_mean_squared_error '). mean ()
    mse. append (score)
    
# Plot cross-validation results    
plt. plot (mse)
plt. xlabel ('Number of Principal Components')
plt. ylabel ('MSE')
plt. title ('hp') 

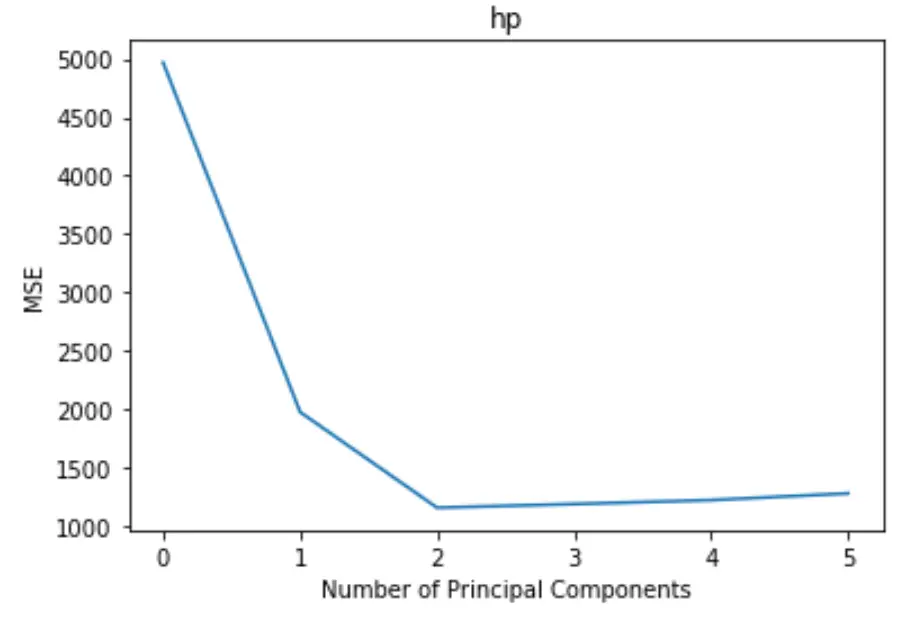
Wykres przedstawia liczbę głównych składników wzdłuż osi x oraz test MSE (średni błąd kwadratowy) wzdłuż osi y.

Z wykresu widzimy, że MSE testu maleje po dodaniu dwóch głównych składników, ale zaczyna rosnąć po dodaniu więcej niż dwóch głównych składników.

Zatem optymalny model obejmuje tylko dwa pierwsze główne elementy.

Możemy również użyć poniższego kodu, aby obliczyć procent wariancji zmiennej odpowiedzi wyjaśnionej poprzez dodanie każdego głównego składnika do modelu:

 n.p. cumsum (np. round (pca. explained_variance_ratio_ , decimals= 4 )* 100 )

array([69.83, 89.35, 95.88, 98.95, 99.99])

Możemy zobaczyć co następuje:

• Używając tylko pierwszego składnika głównego, możemy wyjaśnić 69,83% zmienności zmiennej odpowiedzi.
• Dodając drugi główny składnik, możemy wyjaśnić 89,35% zmienności zmiennej odpowiedzi.

Należy zauważyć, że nadal będziemy w stanie wyjaśnić większą wariancję, używając większej liczby głównych składników, ale widzimy, że dodanie więcej niż dwóch głównych składników w rzeczywistości nie zwiększa znacząco procentu wyjaśnionej wariancji.

Krok 4: Użyj ostatecznego modelu do przewidywania

Możemy wykorzystać ostateczny dwugłówny model PCR do przewidywania nowych obserwacji.

Poniższy kod pokazuje, jak podzielić oryginalny zbiór danych na zbiór uczący i testowy oraz użyć modelu PCR z dwoma głównymi składnikami do przewidywania zbioru testowego.

 #split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size= 0.3 , random_state= 0 ) 

#scale the training and testing data
X_reduced_train = pca. fit_transform ( scale (X_train))
X_reduced_test = pca. transform ( scale (X_test))[:,:1]

#train PCR model on training data 
regr = LinearRegression()
reg. fit (X_reduced_train[:,:1], y_train)

#calculate RMSE
pred = regr. predict (X_reduced_test)
n.p. sqrt ( mean_squared_error (y_test, pred))

40.2096

Widzimy, że test RMSE okazuje się wynosić 40,2096 . Jest to średnie odchylenie pomiędzy przewidywaną wartością KM a obserwowaną wartością KM dla obserwacji zestawu testowego.

Pełny kod Pythona użyty w tym przykładzie można znaleźć tutaj .