Jak przeprowadzić regresję krokową w sas-ie (z przykładem)

Regresja krokowa to procedura, którą możemy zastosować do zbudowania modelu regresji na podstawie zbioru zmiennych predykcyjnych poprzez stopniowe wprowadzanie i usuwanie predyktorów w modelu, aż do momentu, gdy nie będzie już statystycznie uzasadnionego powodu do wprowadzania lub usuń więcej.

Celem regresji krokowej jest utworzenie modelu regresji obejmującego wszystkie zmienne predykcyjne, które są statystycznie istotnie powiązane ze zmienną odpowiedzi .

Aby wykonać regresję krokową w SAS-ie, możesz użyć PROC REG z instrukcją SELECTION .

Poniższy przykład pokazuje, jak w praktyce przeprowadzić regresję krokową w SAS-ie.

Przykład: wykonywanie regresji krok po kroku w SAS-ie

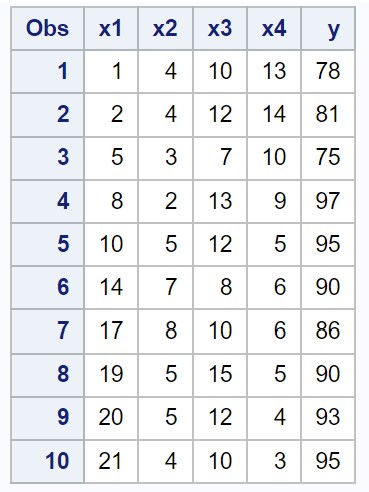
Załóżmy, że mamy następujący zbiór danych w SAS-ie, który zawiera cztery zmienne predykcyjne (x1, x2, x3, x4) i jedną zmienną odpowiedzi (y):

 /*create dataset*/
data my_data;
    input x1 x2 x3 x4 y;
    datalines ;
1 4 10 13 78
2 4 12 14 81
5 3 7 10 75
8 2 13 9 97
10 5 12 5 95
14 7 8 6 90
17 8 10 6 86 
19 5 15 5 90
20 5 12 4 93
21 4 10 3 95
;
run ;

/*view dataset*/
proc print data =my_data;

Załóżmy teraz, że chcemy określić, która kombinacja zmiennych predykcyjnych da najlepszy model regresji liniowej wielokrotnej .

Kiedy mówimy o „najlepszym” modelu regresji, mamy na myśli model, który maksymalizuje lub minimalizuje pewne miary.

Istnieją dwie metryki, których powszechnie używamy do oceny, który model regresji jest najlepszy spośród grupy potencjalnych modeli:

1. Skorygowana wartość R-kwadrat : Skorygowana wartość R-kwadrat mówi nam o użyteczności modelu, skorygowanej na podstawie liczby predyktorów w modelu. Model z najwyższą skorygowaną wartością R-kwadrat jest uważany za najlepszy.

2. AIC : Kryterium informacyjne Akaike (AIC) to metryka używana do porównywania dopasowania różnych modeli regresji. Za najlepszy uważa się model o najniższej wartości AIC.

Na szczęście możemy obliczyć zarówno dopasowane wartości R-kwadrat, jak i AIC dla modeli regresji w SAS za pomocą PROC REG z instrukcją SELECTION .

Poniższy kod pokazuje, jak to zrobić:

 /*perform stepwise multiple linear regression*/
proc reg data =my_data outest =est;
    model y=x1 x2 x3 x4 / selection=adjrsq aic ;
    output out =out p=pr=r;
run ;
quit ; 

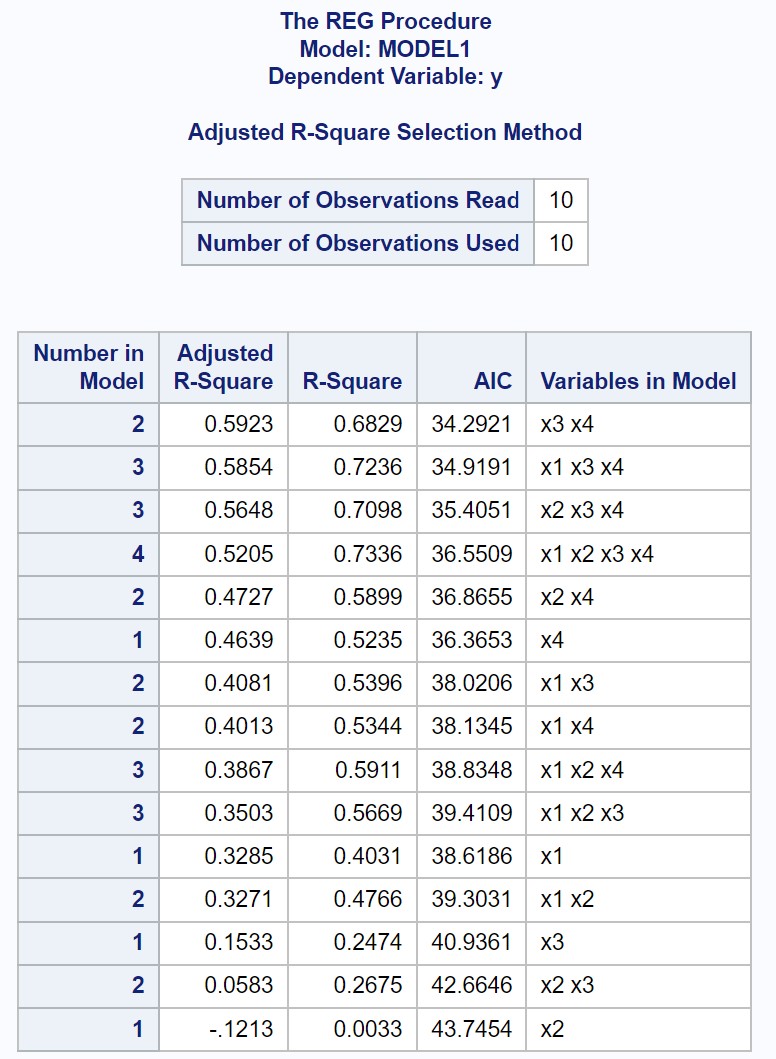
Dane wyjściowe wyświetlają dopasowane wartości R-kwadrat i AIC dla każdego możliwego modelu wielokrotnej regresji liniowej.

Z wyniku widać, że wartość o najwyższej skorygowanej wartości R-kwadrat i najniższej wartości AIC to model regresji, który wykorzystuje wyłącznie x3 i x4 jako zmienne predykcyjne.

Tym samym deklarujemy, że następujący model jest „najlepszy” spośród wszystkich możliwych modeli:

y = b ₀ + b ₁ (x3) + b ₂ (x4)

Ten konkretny model regresji ma następujące metryki:

• Skorygowana wartość R-kwadrat: 0,5923
• AI: 34,2921

Uwagi dotyczące wyboru „najlepszego” modelu regresji

Należy zauważyć, że czasami model z najwyższą skorygowaną wartością R-kwadrat nie zawsze ma również najniższą wartość AIC.

Jeśli chodzi o podjęcie decyzji, który model regresji jest najlepszy, skorygowane R-kwadrat i AIC służą jako sugestie, ale w prawdziwym świecie konieczne może być skorzystanie z wiedzy specjalistycznej w danej dziedzinie, aby określić, który model jest najlepszy.

Rozsądne może być także wybranie modelu oszczędnego , czyli takiego, który osiąga pożądany poziom dopasowania przy użyciu jak najmniejszej liczby zmiennych predykcyjnych.

Uzasadnienie tego typu modelu wywodzi się z idei brzytwy Ockhama (czasami nazywanej „zasadą oszczędności”), która mówi, że najprostsze wyjaśnienie jest prawdopodobnie właściwe.

W odniesieniu do statystyk model, który ma niewiele parametrów, ale osiąga zadowalający poziom dopasowania, powinien być preferowany w porównaniu z modelem, który ma mnóstwo parametrów i osiąga jedynie nieco wyższy poziom dopasowania.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w SAS-ie:

Jak wykonać prostą regresję liniową w SAS-ie
Jak wykonać wielokrotną regresję liniową w SAS-ie
Jak wykonać regresję wielomianową w SAS-ie
Jak przeprowadzić regresję logistyczną w SAS-ie