Jak wykonać regresję kwadratową w r

Kiedy dwie zmienne mają związek liniowy, często możemy zastosować prostą regresję liniową , aby określić ilościowo ich związek.

Jeśli jednak dwie zmienne mają związek kwadratowy, możemy zastosować regresję kwadratową do ilościowego określenia ich związku.

W tym samouczku wyjaśniono, jak przeprowadzić regresję kwadratową w języku R.

Przykład: regresja kwadratowa w R

Załóżmy, że chcemy zrozumieć związek pomiędzy liczbą przepracowanych godzin a zgłaszanym szczęściem. Mamy następujące dane dotyczące liczby godzin przepracowanych tygodniowo i zgłaszanego poziomu szczęścia (w skali od 0 do 100) dla 11 różnych osób:

Wykonaj poniższe kroki, aby dopasować model regresji kwadratowej w R.

Krok 1: Wprowadź dane.

Najpierw utworzymy ramkę danych zawierającą nasze dane:

 #createdata
data <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                   happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))

#viewdata 
data

   hours happiness
1 6 14
2 9 28
3 12 50
4 14 70
5 30 89
6 35 94
7 40 90
8 47 75
9 51 59
10 55 44
11 60 27

Krok 2: Wizualizuj dane.

Następnie utworzymy prosty wykres rozrzutu do wizualizacji danych.

 #create scatterplot
plot(data$hours, data$happiness, pch=16) 

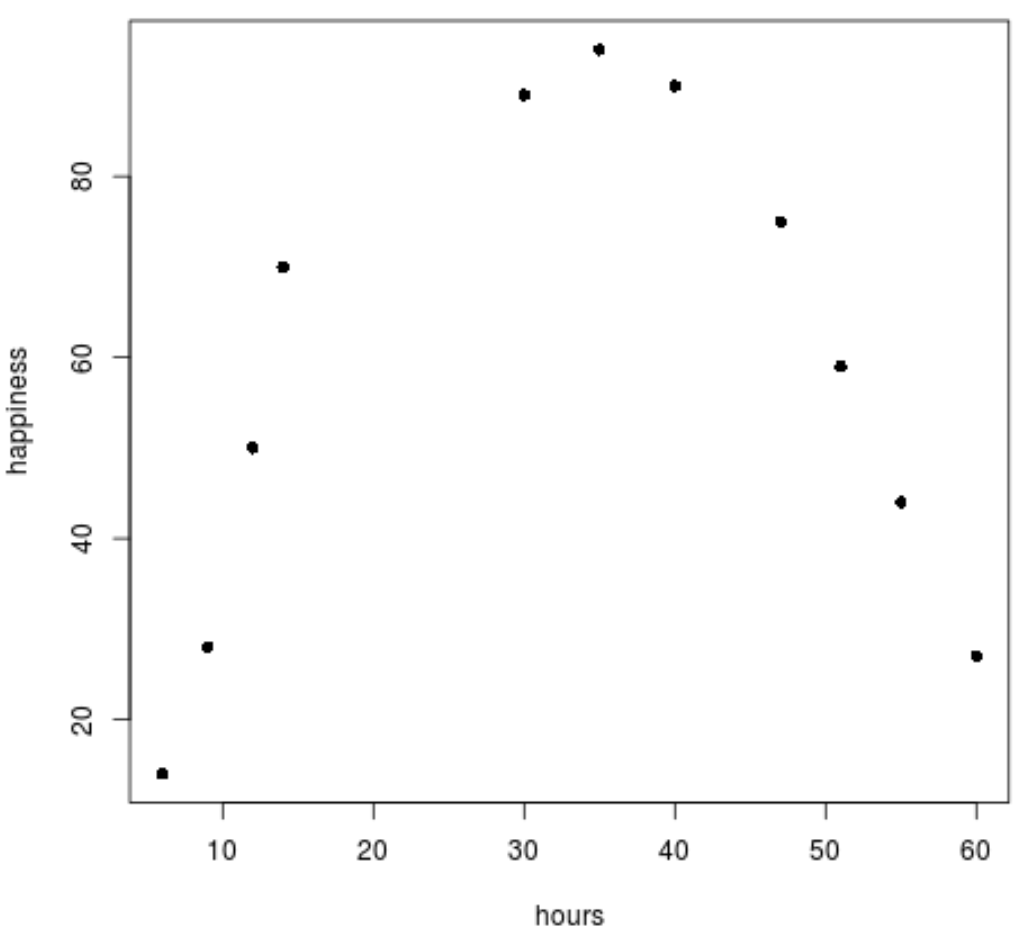
Wyraźnie widać, że dane nie układają się według liniowego wzorca.

Krok 3: Dopasuj prosty model regresji liniowej.

Następnie dopasujemy prosty model regresji liniowej, aby sprawdzić, jak dobrze pasuje on do danych:

 #fit linear model
linearModel <- lm(happiness ~ hours, data=data)

#view model summary
summary(linearModel)

Call:
lm(formula = happiness ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-39.34 -21.99 -2.03 23.50 35.11 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept) 48.4531 17.3288 2.796 0.0208 *
hours 0.2981 0.4599 0.648 0.5331  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 28.72 on 9 degrees of freedom
Multiple R-squared: 0.0446, Adjusted R-squared: -0.06156 
F-statistic: 0.4201 on 1 and 9 DF, p-value: 0.5331

Całkowita wariancja szczęścia wyjaśniona przez model wynosi tylko 4,46% , jak pokazuje wielokrotna wartość R-kwadrat.

Krok 4: Dopasuj model regresji kwadratowej.

Następnie dopasujemy model regresji kwadratowej.

 #create a new variable for hours 2
data$hours2 <- data$hours^2

#fit quadratic regression model
quadraticModel <- lm(happiness ~ hours + hours2, data=data)

#view model summary
summary(quadraticModel)

Call:
lm(formula = happiness ~ hours + hours2, data = data)

Residuals:
    Min 1Q Median 3Q Max 
-6.2484 -3.7429 -0.1812 1.1464 13.6678 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.218 on 8 degrees of freedom
Multiple R-squared: 0.9602, Adjusted R-squared: 0.9502 
F-statistic: 96.49 on 2 and 8 DF, p-value: 2.51e-06

Całkowita wariancja szczęścia wyjaśniona przez model wzrosła do 96,02% .

Możemy użyć poniższego kodu, aby zwizualizować stopień dopasowania modelu do danych:

 #create sequence of hour values
hourValues <- seq(0, 60, 0.1)

#create list of predicted happiness levels using quadratic model
happinessPredict <- predict(quadraticModel, list(hours=hourValues, hours2=hourValues^2))

#create scatterplot of original data values
plot(data$hours, data$happiness, pch=16)
#add predicted lines based on quadratic regression model
lines(hourValues, happinessPredict, col='blue')

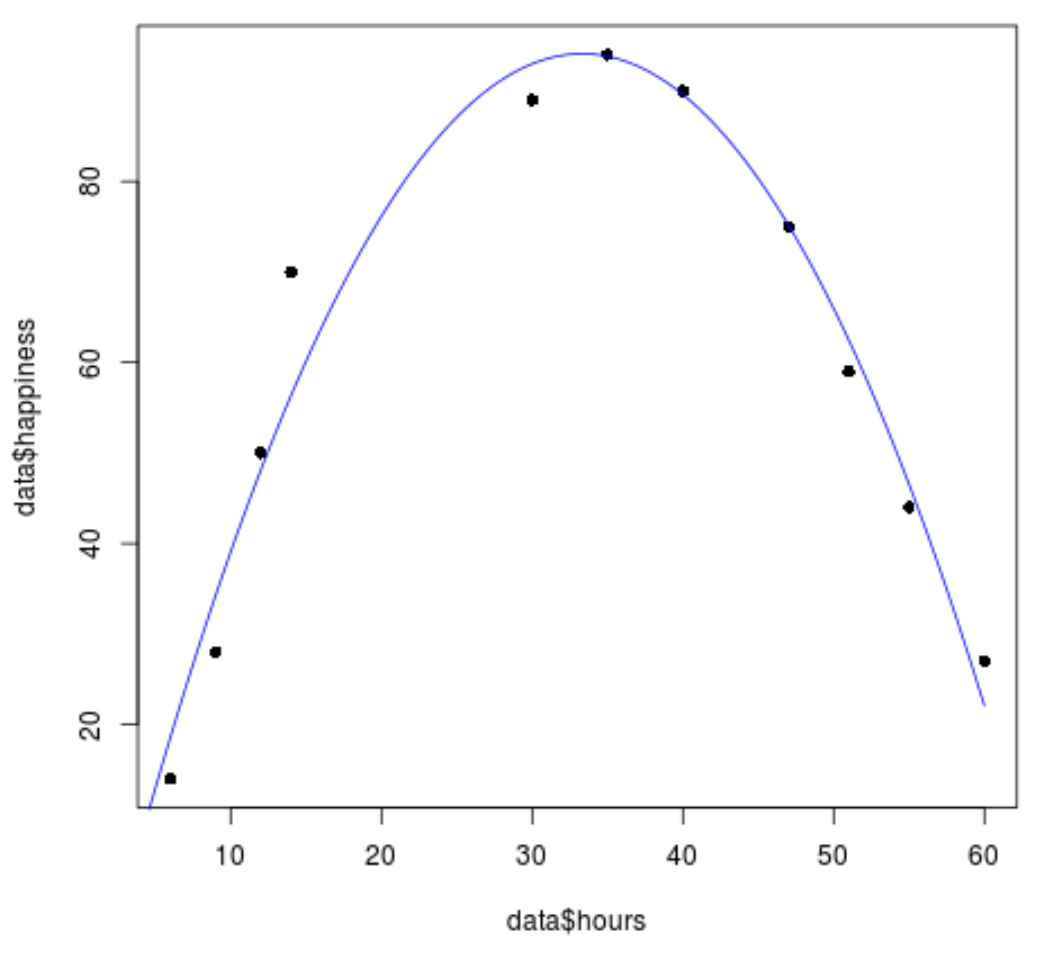
Widzimy, że linia regresji kwadratowej całkiem dobrze pasuje do wartości danych.

Krok 5: Interpretacja modelu regresji kwadratowej.

W poprzednim kroku widzieliśmy, że wynikiem modelu regresji kwadratowej był:

 Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***

W oparciu o przedstawione tutaj współczynniki skorygowana regresja kwadratowa będzie wynosić:

Szczęście = -0,1012 (godziny) ² + 6,7444 (godziny) – 18,2536

Możemy użyć tego równania, aby znaleźć przewidywane szczęście danej osoby, biorąc pod uwagę liczbę godzin przepracowanych w tygodniu.

Na przykład osoba pracująca 60 godzin tygodniowo miałaby poziom szczęścia równy 22,09 :

Szczęście = -0,1012(60) ² + 6,7444(60) – 18,2536 = 22,09

I odwrotnie, osoba pracująca 30 godzin tygodniowo powinna mieć poziom szczęścia na poziomie 92,99 :

Szczęście = -0,1012(30) ² + 6,7444(30) – 18,2536 = 92,99