Jak wykonać regresję kwantylową w pythonie

Regresja liniowa to metoda, którą możemy wykorzystać do zrozumienia związku między jedną lub większą liczbą zmiennych predykcyjnych azmienną odpowiedzi .

Zwykle, gdy przeprowadzamy regresję liniową, chcemy oszacować średnią wartość zmiennej odpowiedzi.

Zamiast tego możemy jednak zastosować metodę znaną jako regresja kwantylowa , aby oszacować dowolną wartość kwantylową lub percentylową wartości odpowiedzi, taką jak 70. percentyl, 90. percentyl, 98. percentyl itp.

W tym samouczku przedstawiono krok po kroku przykład użycia tej funkcji do przeprowadzenia regresji kwantylowej w języku Python.

Krok 1: Załaduj niezbędne pakiety

Najpierw załadujemy niezbędne pakiety i funkcje:

 import numpy as np
import pandas as pd
import statsmodels. api as sm
import statsmodels. formula . api as smf
import matplotlib. pyplot as plt

Krok 2: Utwórz dane

Dla tego przykładu utworzymy zbiór danych zawierający przepracowane godziny i wyniki egzaminów uzyskane dla 100 studentów na uczelni:

 #make this example reproducible
n.p. random . seeds (0)

#create dataset
obs = 100

hours = np. random . uniform (1, 10, obs)
score = 60 + 2*hours + np. random . normal (loc=0, scale=.45*hours, size=100)

df = pd. DataFrame ({' hours ':hours, ' score ':score})

#view first five rows
df. head ()

hours score
0 5.939322 68.764553
1 7.436704 77.888040
2 6.424870 74.196060
3 5.903949 67.726441
4 4.812893 72.849046

Krok 3: Wykonaj regresję kwantylową

Następnie dopasujemy model regresji kwantylowej, wykorzystując przestudiowane godziny jako zmienną predykcyjną i wyniki egzaminów jako zmienną odpowiedzi.

Wykorzystamy ten model do przewidzenia oczekiwanego 90. percentyla wyników egzaminu na podstawie liczby przepracowanych godzin:

 #fit the model
model = smf. quantreg ('score~hours', df). fit (q= 0.9 )

#view model summary
print ( model.summary ())

                         QuantReg Regression Results                          
==================================================== ============================
Dept. Variable: Pseudo R-squared score: 0.6057
Model: QuantReg Bandwidth: 3.822
Method: Least Squares Sparsity: 10.85
Date: Tue, 29 Dec 2020 No. Observations: 100
Time: 15:41:44 Df Residuals: 98
                                        Model: 1
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
Intercept 59.6104 0.748 79.702 0.000 58.126 61.095
hours 2.8495 0.128 22.303 0.000 2.596 3.103
==================================================== ============================

Z wyniku możemy zobaczyć oszacowane równanie regresji:

90. percentyl wyniku egzaminu = 59,6104 + 2,8495*(godziny)

Na przykład 90. percentyl wyniku wszystkich uczniów, którzy uczą się 8 godzin, powinien wynosić 82,4:

90. percentyl wyniku egzaminu = 59,6104 + 2,8495*(8) = 82,4 .

Dane wyjściowe wyświetlają także górną i dolną granicę ufności dla wyrazu wolnego oraz czasy zmiennej predykcyjnej.

Krok 4: Wizualizuj wyniki

Możemy również wizualizować wyniki regresji, tworząc wykres rozrzutu z dopasowanym równaniem regresji kwantylowej nałożonym na wykres:

 #define figure and axis
fig, ax = plt.subplots(figsize=(8, 6))

#get y values
get_y = lambda a, b: a + b * hours
y = get_y( model.params [' Intercept '], model.params [' hours '])

#plot data points with quantile regression equation overlaid
ax. plot (hours, y, color=' black ')
ax. scatter (hours, score, alpha=.3)
ax. set_xlabel (' Hours Studied ', fontsize=14)
ax. set_ylabel (' Exam Score ', fontsize=14)

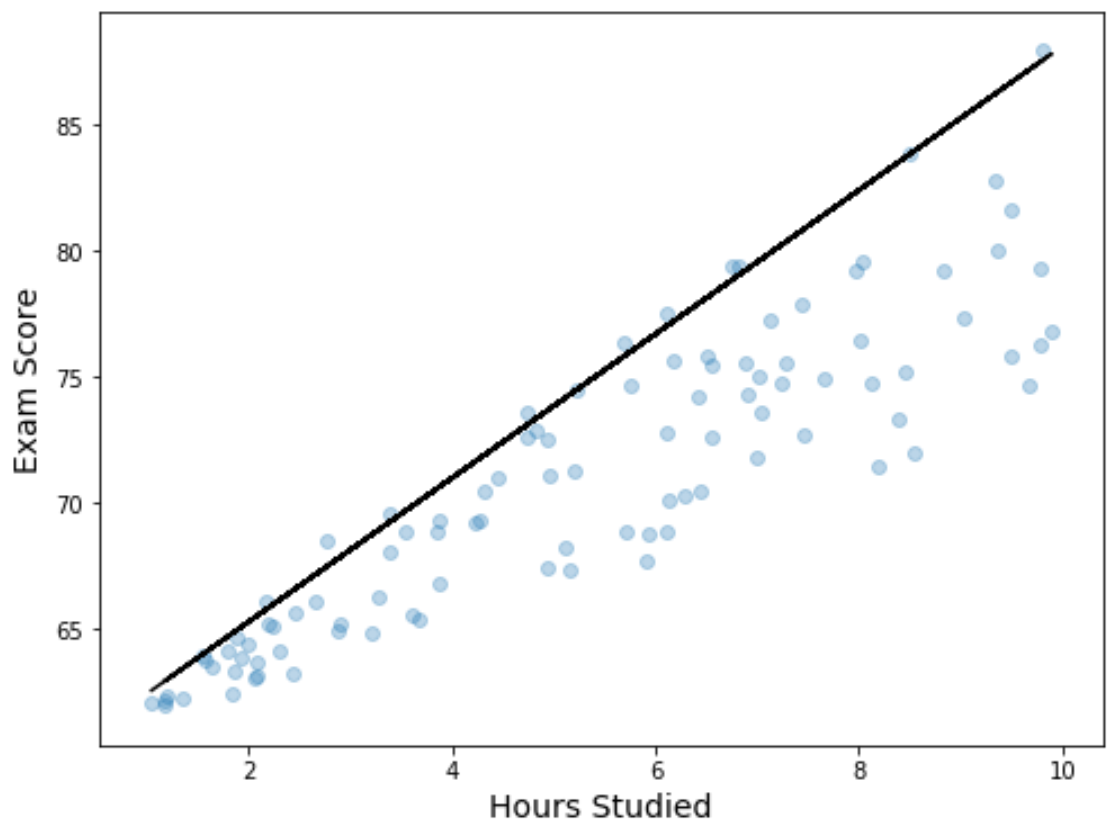
W przeciwieństwie do prostej linii regresji liniowej należy pamiętać, że ta dopasowana linia nie reprezentuje „linii najlepszego dopasowania” danych. Zamiast tego przechodzi przez szacunkowy 90. percentyl na każdym poziomie zmiennej predykcyjnej.

Dodatkowe zasoby

Jak wykonać prostą regresję liniową w Pythonie
Jak wykonać regresję kwadratową w Pythonie