Jak przeprowadzić regresję kwantylową w r

Regresja liniowa to metoda, którą możemy wykorzystać do zrozumienia związku między jedną lub większą liczbą zmiennych predykcyjnych azmienną odpowiedzi .

Zwykle, gdy przeprowadzamy regresję liniową, chcemy oszacować średnią wartość zmiennej odpowiedzi.

Zamiast tego możemy jednak zastosować metodę znaną jako regresja kwantylowa , aby oszacować dowolną wartość kwantylową lub percentylową wartości odpowiedzi, taką jak 70. percentyl, 90. percentyl, 98. percentyl itp.

Aby wykonać regresję kwantylową w R, możemy użyć funkcji rq() z pakietu quantreg , która wykorzystuje następującą składnię:

 library (quantreg)

model <- rq(y ~ x, data = dataset, tau = 0.5 )

Złoto:

• y: zmienna odpowiedzi
• x: zmienne predykcyjne
• dane: nazwa zbioru danych
• tau: percentyl do znalezienia. Wartość domyślna to mediana (tau = 0,5), ale można ją ustawić na dowolną liczbę z zakresu od 0 do 1.

W tym samouczku przedstawiono krok po kroku przykład użycia tej funkcji do przeprowadzenia regresji kwantylowej w języku R.

Krok 1: Wprowadź dane

Na potrzeby tego przykładu utworzymy zbiór danych zawierający przepracowane godziny i wyniki egzaminów uzyskane dla 100 różnych studentów na uczelni:

 #make this example reproducible
set.seed(0)

#create data frame 
hours <- runif(100, 1, 10)
score <- 60 + 2*hours + rnorm(100, mean=0, sd=.45*hours)
df <- data.frame(hours, score)

#view first six rows
head(df)

     hours score
1 9.070275 79.22682
2 3.389578 66.20457
3 4.349115 73.47623
4 6.155680 70.10823
5 9.173870 78.12119
6 2.815137 65.94716

Krok 2: Wykonaj regresję kwantylową

Następnie dopasujemy model regresji kwantylowej, wykorzystując przestudiowane godziny jako zmienną predykcyjną i wyniki egzaminów jako zmienną odpowiedzi.

Wykorzystamy ten model do przewidzenia oczekiwanego 90. percentyla wyników egzaminu na podstawie liczby przepracowanych godzin:

 library (quantreg)

#fit model
model <- rq(score ~ hours, data = df, tau = 0.9 )

#view summary of model
summary(model)

Call: rq(formula = score ~ hours, tau = 0.9, data = df)

tau: [1] 0.9

Coefficients:
            coefficients lower bd upper bd
(Intercept) 60.25185 59.27193 62.56459
hours 2.43746 1.98094 2.76989

Z wyniku możemy zobaczyć oszacowane równanie regresji:

Wynik egzaminu na 90. percentylu = 60,25 + 2,437*(godziny)

Na przykład 90. percentyl wyniku dla wszystkich uczniów, którzy uczą się 8 godzin, powinien wynosić 79,75:

90. percentyl wyniku egzaminu = 60,25 + 2,437*(8) = 79,75 .

Dane wyjściowe wyświetlają także górną i dolną granicę ufności dla wyrazu wolnego oraz czasy zmiennej predykcyjnej.

Krok 3: Wizualizuj wyniki

Możemy również wizualizować wyniki regresji, tworząc wykres rozrzutu z dopasowanym równaniem regresji kwantylowej nałożonym na wykres:

 library (ggplot2)

#create scatterplot with quantile regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) 

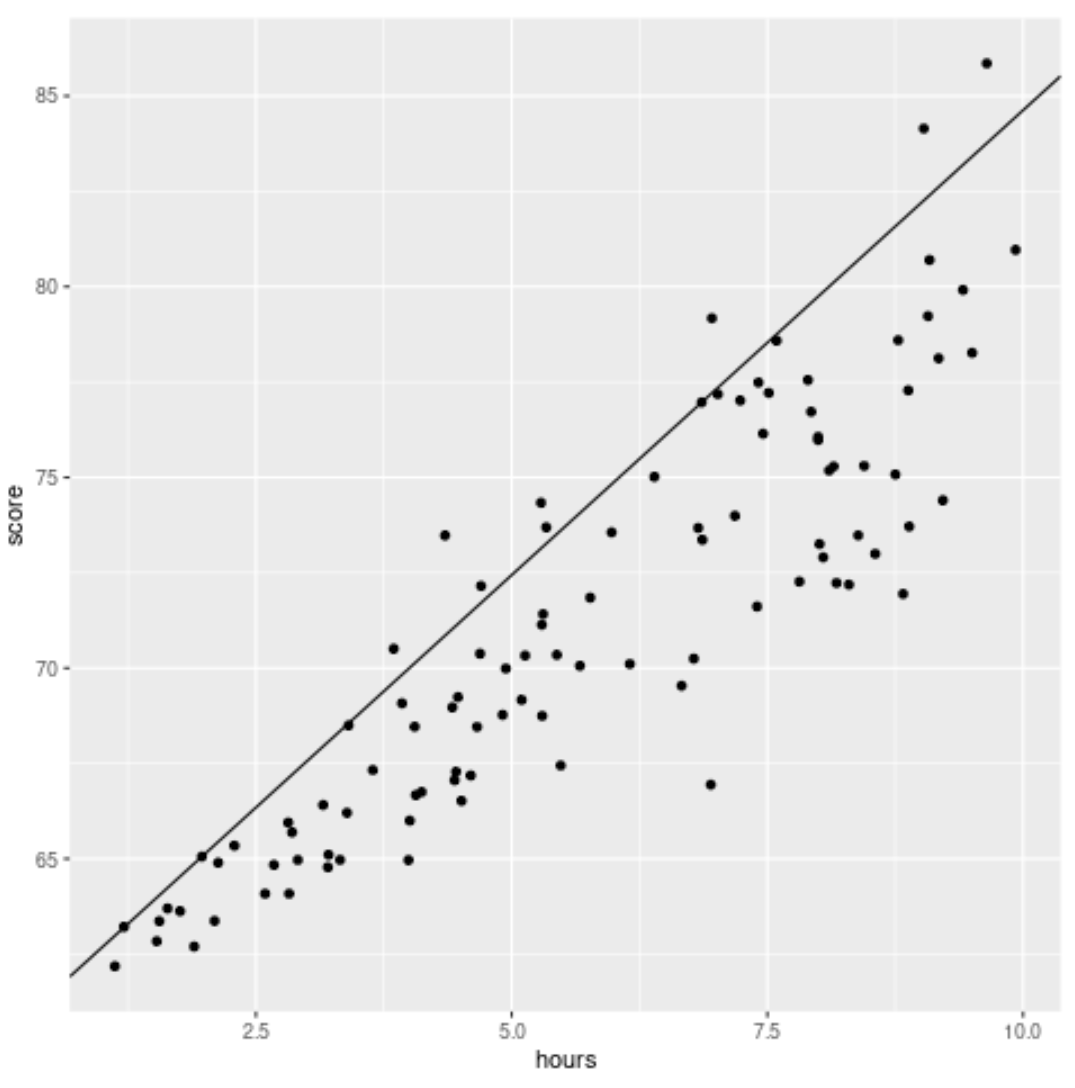
W przeciwieństwie do tradycyjnej linii regresji liniowej należy pamiętać, że dopasowana linia nie przechodzi przez serce danych. Zamiast tego przechodzi przez szacunkowy 90. percentyl na każdym poziomie zmiennej predykcyjnej.

Różnicę między dopasowanym równaniem regresji kwantylowej a prostym równaniem regresji liniowej możemy zobaczyć, dodając argument geom_smooth() :

 library (ggplot2)

#create scatterplot with quantile regression line and simple linear regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) +
  geom_smooth(method=" lm ", se= F ) 

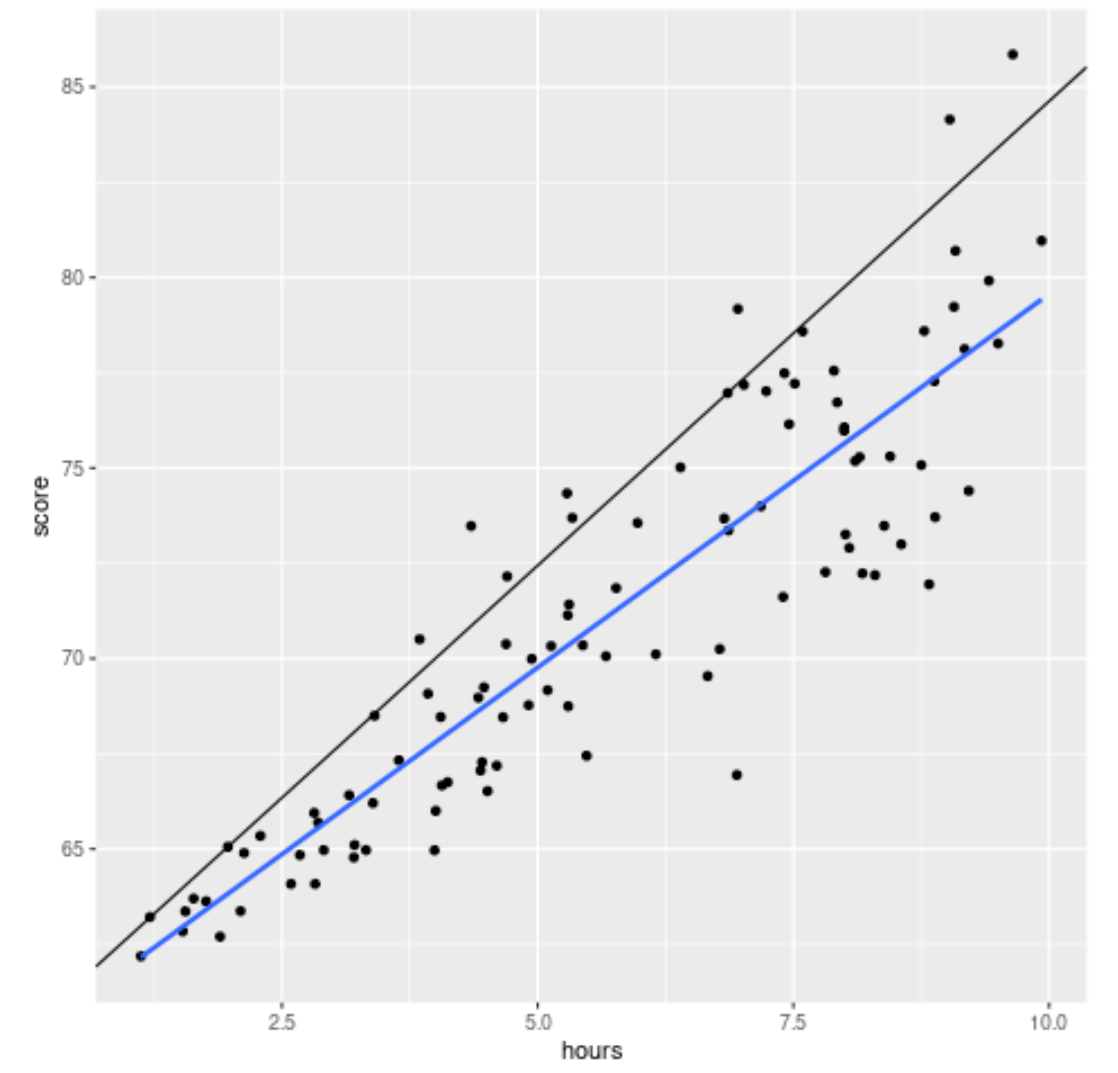
Czarna linia przedstawia linię regresji kwantylowej skorygowaną dla 90. percentyla, a niebieska linia przedstawia prostą linię regresji liniowej, która szacuje średnią wartość zmiennej odpowiedzi.

Zgodnie z oczekiwaniami prosta linia regresji liniowej przebiega przez dane i pokazuje nam szacunkową średnią wartość wyników egzaminów na każdym poziomie godzinowym.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w języku R:

Jak wykonać prostą regresję liniową w R
Jak wykonać wielokrotną regresję liniową w R
Jak wykonać regresję kwadratową w R