Wprowadzenie do regresji lasso

W zwykłej wielokrotnej regresji liniowej używamy zestawu p zmiennych predykcyjnych i zmiennej odpowiedzi , aby dopasować model w postaci:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

Złoto:

• Y : Zmienna odpowiedzi
• X _j : j- ^ta zmienna predykcyjna
• β _j : Średni wpływ na Y jednojednostkowego wzrostu X _j , przy założeniu, że wszystkie inne predyktory są stałe
• ε : Termin błędu

Wartości β ₀ , β ₁ , B ₂ , …, β _p dobieramy metodą najmniejszych kwadratów , która minimalizuje sumę kwadratów reszt (RSS):

RSS = Σ(y _i – ŷ _i ) ²

Złoto:

• Σ : Grecki symbol oznaczający sumę
• y _i : rzeczywista wartość odpowiedzi dla ^i-tej obserwacji
• ŷ _i : Przewidywana wartość odpowiedzi na podstawie modelu wielokrotnej regresji liniowej

Jednakże, gdy zmienne predykcyjne są silnie skorelowane, współliniowość może stać się problemem. Może to sprawić, że szacunki współczynników modelu będą niewiarygodne i będą wykazywać dużą wariancję. Oznacza to, że gdy model zostanie zastosowany do nowego zbioru danych, którego nigdy wcześniej nie widział, prawdopodobnie będzie działał słabo.

Jednym ze sposobów obejścia tego problemu jest użycie metody znanej jako regresja lasso , która zamiast tego ma na celu zminimalizowanie następujących elementów:

RSS + λΣ|β _j |

gdzie j przechodzi od 1 do p i λ ≥ 0.

Ten drugi człon równania nazywany jest karą za wycofanie .

Gdy λ = 0, ten składnik kary nie ma żadnego efektu, a regresja lasso daje takie same szacunki współczynników, jak metoda najmniejszych kwadratów.

Jednakże, gdy λ zbliża się do nieskończoności, kara za usunięcie staje się bardziej wpływowa, a zmienne predykcyjne, których nie można zaimportować do modelu, są redukowane do zera, a niektóre nawet usuwane z modelu.

Dlaczego warto stosować regresję Lasso?

Przewagą regresji lasso nad regresją metodą najmniejszych kwadratów jest kompromis w zakresie odchylenia i wariancji .

Przypomnijmy, że błąd średniokwadratowy (MSE) to metryka, za pomocą której możemy zmierzyć dokładność danego modelu i oblicza się go w następujący sposób:

MSE = Var( f̂( x ₀ )) + [Odchylenie( f̂( x ₀ ))] ² + Var(ε)

MSE = wariancja + błąd ² + błąd nieredukowalny

Podstawową ideą regresji lasso jest wprowadzenie małego błędu systematycznego, dzięki czemu wariancja może zostać znacznie zmniejszona, co prowadzi do niższego ogólnego MSE.

Aby to zilustrować, rozważ następujący wykres:

Należy zauważyć, że wraz ze wzrostem λ wariancja znacznie maleje przy bardzo małym wzroście obciążenia. Jednak powyżej pewnego punktu wariancja maleje wolniej, a spadek współczynników prowadzi do ich znacznego niedoszacowania, co prowadzi do gwałtownego wzrostu obciążenia systematycznego.

Z wykresu widzimy, że MSE testu jest najniższe, gdy wybierzemy wartość λ, która zapewnia optymalny kompromis między obciążeniem a wariancją.

Gdy λ = 0, składnik karny w regresji lasso nie ma żadnego efektu i dlatego daje takie same oszacowania współczynników, jak metoda najmniejszych kwadratów. Jednakże, zwiększając λ do pewnego punktu, możemy zmniejszyć całkowite MSE testu.

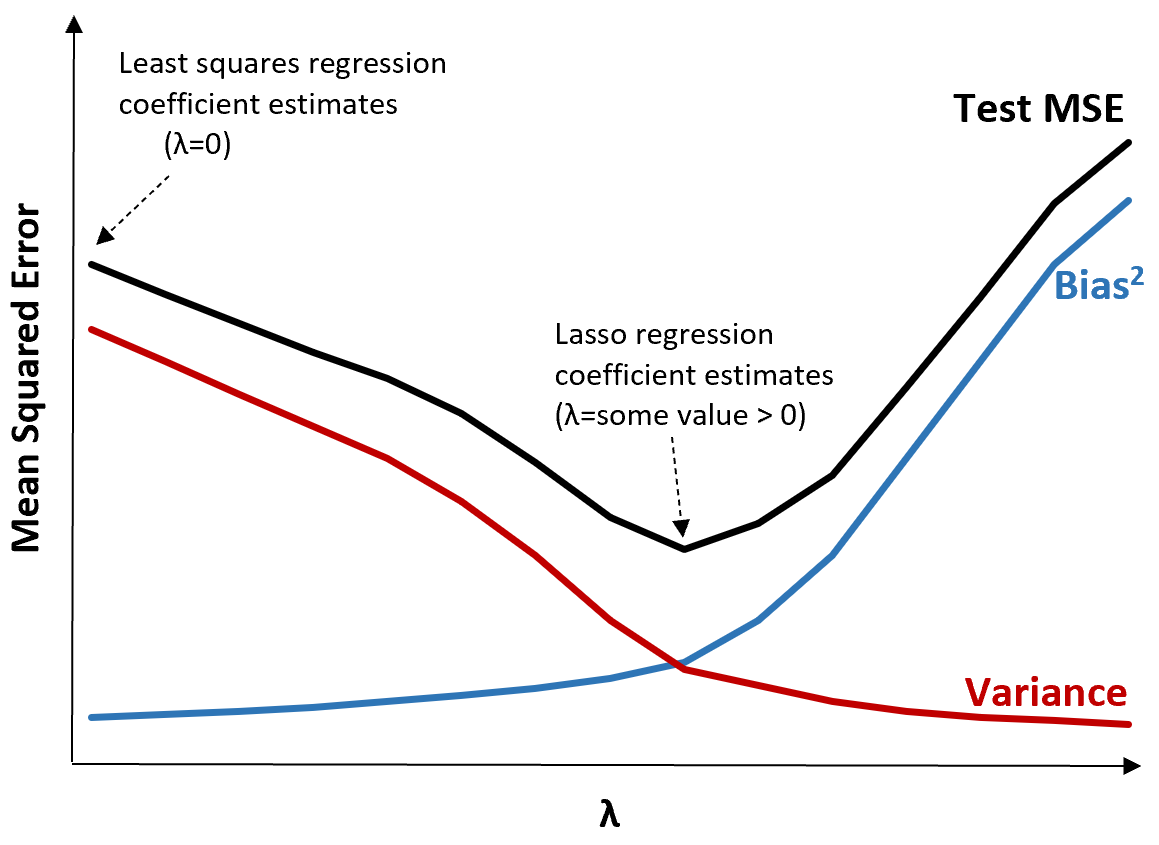
Oznacza to, że dopasowanie modelu metodą regresji lasso będzie skutkowało mniejszymi błędami testowymi niż dopasowanie modelu metodą najmniejszych kwadratów.

Regresja Lasso a regresja Ridge’a

Zarówno regresja Lasso, jak i regresja Ridge’a są znane jako metody regularyzacji , ponieważ obie mają na celu zminimalizowanie resztowej sumy kwadratów (RSS), a także określonego warunku kary.

Innymi słowy, ograniczają lub regulują oszacowania współczynników modelu.

Jednak stosowane przez nich warunki kar są nieco inne:

• Regresja Lasso próbuje zminimalizować RSS + λΣ|β _j |
• Regresja grzbietowa próbuje zminimalizować RSS + λΣβ _j ²

Kiedy używamy regresji grzbietowej, współczynniki każdego predyktora są redukowane do zera, ale żaden z nich nie może całkowicie spaść do zera .

I odwrotnie, gdy zastosujemy regresję lasso, możliwe jest, że niektóre współczynniki staną się całkowicie zerowe , gdy λ stanie się wystarczająco duże.

Z technicznego punktu widzenia regresja lasso umożliwia tworzenie modeli „rzadkich”, to znaczy modeli zawierających tylko podzbiór zmiennych predykcyjnych.

Nasuwa się pytanie: czy lepsza jest regresja grzbietu czy regresja lasso?

Odpowiedź: to zależy!

W przypadkach, gdy istotna jest tylko niewielka liczba zmiennych predykcyjnych, regresja lasso zwykle działa lepiej, ponieważ jest w stanie całkowicie zredukować nieistotne zmienne do zera i usunąć je z modelu.

Jednakże, gdy w modelu znaczących jest wiele zmiennych predykcyjnych, a ich współczynniki są w przybliżeniu równe, regresja grzbietowa zwykle działa lepiej, ponieważ utrzymuje wszystkie predyktory w modelu.

Aby określić, który model jest najskuteczniejszy w przewidywaniu, przeprowadzamy k-krotną weryfikację krzyżową . Najlepszym modelem jest model, który generuje najniższy błąd średniokwadratowy (MSE).

Etapy wykonywania regresji lasso w praktyce

Aby przeprowadzić regresję lasso, można wykonać następujące kroki:

Krok 1: Oblicz macierz korelacji i wartości VIF dla zmiennych predykcyjnych.

Najpierw musimy stworzyć macierz korelacji i obliczyć wartości VIF (współczynnik inflacji wariancji) dla każdej zmiennej predykcyjnej.

Jeśli wykryjemy silną korelację między zmiennymi predykcyjnymi a wysokimi wartościami VIF (niektóre teksty definiują „wysoką” wartość VIF na 5, podczas gdy inne używają 10), wówczas prawdopodobnie właściwa będzie regresja lasso.

Jeśli jednak w danych nie występuje współliniowość, wykonywanie regresji lasso może nie być konieczne. Zamiast tego możemy wykonać zwykłą regresję metodą najmniejszych kwadratów.

Krok 2: Dopasuj model regresji lasso i wybierz wartość λ.

Kiedy już ustalimy, że regresja lasso jest właściwa, możemy dopasować model (używając popularnych języków programowania, takich jak R czy Python), stosując optymalną wartość λ.

Aby określić optymalną wartość λ, możemy dopasować wiele modeli, stosując różne wartości λ i wybrać λ jako wartość, która daje najniższy test MSE.

Krok 3: Porównaj regresję lassa z regresją grzbietową i zwykłą regresją metodą najmniejszych kwadratów.

Na koniec możemy porównać nasz model regresji lasso z modelem regresji grzbietowej i modelem regresji metodą najmniejszych kwadratów, aby określić, który model daje najniższy test MSE przy użyciu k-krotnej walidacji krzyżowej.

W zależności od relacji między zmiennymi predykcyjnymi a zmienną odpowiedzi jest całkowicie możliwe, że jeden z tych trzech modeli będzie lepszy od pozostałych w różnych scenariuszach.

Regresja Lasso w R i Pythonie

Poniższe samouczki wyjaśniają, jak przeprowadzić regresję lasso w R i Pythonie:

Regresja Lasso w R (krok po kroku)
Regresja Lasso w Pythonie (krok po kroku)