Jak wykonać regresję loess w r (z przykładem)

Regresja LOESS , czasami nazywana regresją lokalną, to metoda wykorzystująca lokalne dostosowanie w celu dopasowania modelu regresji do zbioru danych.

Poniższy przykład pokazuje krok po kroku, jak przeprowadzić regresję LOESS w R.

Krok 1: Utwórz dane

Najpierw utwórzmy następującą ramkę danych w R:

 #view DataFrame
df <- data. frame (x=c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14),
                 y=c(1, 4, 7, 13, 19, 24, 20, 15, 13, 11, 15, 18, 22, 27))

#view first six rows of data frame
head(df)

  xy
1 1 1
2 2 4
3 3 7
4 4 13
5 5 19
6 6 24

Krok 2: Dopasuj wiele modeli regresji LOESS

Możemy użyć funkcji loess() , aby dopasować do tego zbioru danych wiele modeli regresji LOESS, stosując różne wartości parametru span :

 #fit several LOESS regression models to dataset
loess50 <- loess(y ~ x, data=df, span= .5 )
smooth50 <- predict(loess50) 

loess75 <- loess(y ~ x, data=df, span= .75 )
smooth75 <- predict(loess75) 

loess90 <- loess(y ~ x, data=df, span= .9 )
smooth90 <- predict(loess90) 

#create scatterplot with each regression line overlaid
plot(df$x, df$y, pch= 19 , main=' Loess Regression Models ')
lines(smooth50, x=df$x, col=' red ')
lines(smooth75, x=df$x, col=' purple ')
lines(smooth90, x=df$x, col=' blue ')
legend(' bottomright ', legend=c(' .5 ', ' .75 ', ' .9 '),
        col=c(' red ', ' purple ', ' blue '), pch= 19 , title=' Smoothing Span ')

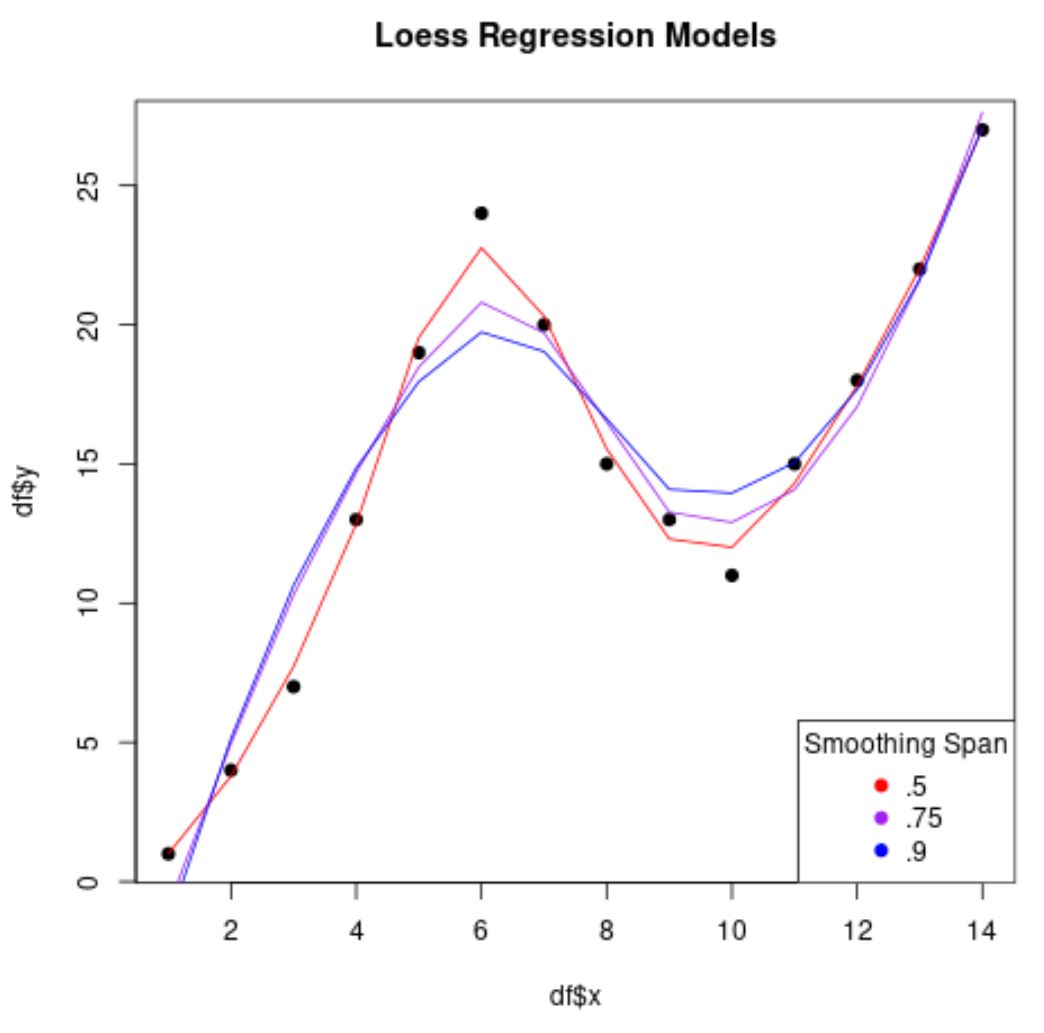
Należy zauważyć, że im niższą wartość zastosujemy dla span , tym mniej „gładki” będzie model regresji i tym bardziej model będzie próbował dopasować punkty danych.

Krok 3: Użyj walidacji krzyżowej typu K, aby znaleźć najlepszy model

Aby znaleźć optymalną wartość zakresu , możemy przeprowadzić k-krotną weryfikację krzyżową , korzystając z funkcji z pakietu caret :

 library (caret)

#define k-fold cross validation method
ctrl <- trainControl(method = " cv ", number = 5 )
grid <- expand. grid (span = seq( 0.5 , 0.9 , len = 5 ), degree = 1 )

#perform cross-validation using smoothing spans ranging from 0.5 to 0.9
model <- train(y ~ x, data = df, method = " gamLoess ", tuneGrid=grid, trControl = ctrl)

#print results of k-fold cross-validation
print (model)

14 samples
 1 predictor

No pre-processing
Resampling: Cross-Validated (5 fold) 
Summary of sample sizes: 12, 11, 11, 11, 11 
Resampling results across tuning parameters:

  span RMSE Rsquared MAE      
  0.5 10.148315 0.9570137 6.467066
  0.6 7.854113 0.9350278 5.343473
  0.7 6.113610 0.8150066 4.769545
  0.8 17.814105 0.8202561 11.875943
  0.9 26.705626 0.7384931 17.304833

Tuning parameter 'degree' was held constant at a value of 1
RMSE was used to select the optimal model using the smallest value.
The final values used for the model were span = 0.7 and degree = 1.

Widzimy, że wartość rozpiętości , która dała najniższą wartość błędu średniokwadratowego (RMSE), wynosi 0,7 .

Zatem w naszym ostatecznym modelu regresji LOESS zdecydowalibyśmy się użyć wartości 0,7 dla argumentu span w funkcji loess() .

Dodatkowe zasoby

Poniższe samouczki zawierają dodatkowe informacje na temat modeli regresji w języku R:

Jak wykonać prostą regresję liniową w R
Jak wykonać wielokrotną regresję liniową w R
Jak przeprowadzić regresję logistyczną w R
Jak przeprowadzić regresję kwantylową w R
Jak przeprowadzić regresję ważoną w R