Wprowadzenie do prostej regresji liniowej

Prosta regresja liniowa to metoda statystyczna, którą można zastosować do zrozumienia związku między dwiema zmiennymi, x i y.

Zmienna x jest nazywana zmienną predykcyjną .

Druga zmienna, y , nazywana jest zmienną odpowiedzi .

Załóżmy na przykład, że mamy następujący zbiór danych zawierający masę i wzrost siedmiu osób:

Niech waga będzie zmienną predykcyjną, a wzrost niech będzie zmienną odpowiedzi.

Jeśli wykreślimy te dwie zmienne za pomocą wykresu rozrzutu, z wagą na osi x i wzrostem na osi y, będzie to wyglądało tak:

Załóżmy, że chcemy zrozumieć związek między wagą a wzrostem. Z wykresu rozrzutu wyraźnie widać, że wraz ze wzrostem masy ciała wzrasta również wzrost, ale aby faktycznie określić ilościowo tę zależność między masą a wzrostem, musimy zastosować regresję liniową.

Korzystając z regresji liniowej, możemy znaleźć linię, która najlepiej „pasuje” do naszych danych. Linię tę nazywa się linią regresji metodą najmniejszych kwadratów i można ją wykorzystać, aby pomóc nam zrozumieć zależności między wagą a wzrostem.

Zwykle do znalezienia równania tej linii będziesz używać oprogramowania takiego jak Microsoft Excel, SPSS lub kalkulatora graficznego.

Zapisano wzór na linię najlepszego dopasowania:

ŷ = b ₀ + b ₁ x

gdzie ŷ to przewidywana wartość zmiennej odpowiedzi, b ₀ to wyraz wolny, b ₁ to współczynnik regresji, a x to wartość zmiennej predykcyjnej.

Powiązane: 4 przykłady zastosowania regresji liniowej w prawdziwym życiu

Znajdź „najlepiej dopasowaną linię”

W tym przykładzie możemy po prostu podłączyć nasze dane do statystycznego kalkulatora regresji liniowej i nacisnąć Oblicz :

Kalkulator automatycznie znajduje linię regresji metodą najmniejszych kwadratów :

ŷ = 32,7830 + 0,2001x

Jeśli pomniejszymy nasz poprzedni wykres rozrzutu i dodamy tę linię do wykresu, będzie to wyglądało tak:

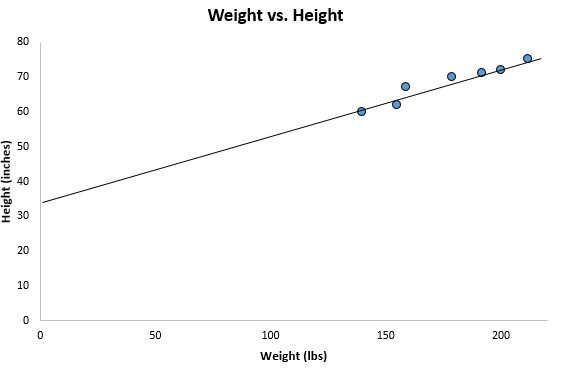
Zwróć uwagę, jak nasze punkty danych są ściśle rozproszone wokół tej linii. Rzeczywiście, ta linia regresji metodą najmniejszych kwadratów jest linią najlepiej pasującą do naszych danych spośród wszystkich możliwych linii, które moglibyśmy narysować.

Jak interpretować linię regresji metodą najmniejszych kwadratów

Oto jak zinterpretować tę linię regresji metodą najmniejszych kwadratów: ŷ = 32,7830 + 0,2001x

_b0 = 32,7830 . Oznacza to, że gdy zmienna waga predyktora wynosi zero funtów, przewidywany wzrost wynosi 32,7830 cali. Czasami warto znać wartość b ₀ , ale w tym konkretnym przykładzie interpretacja b ₀ nie ma sensu, ponieważ dana osoba nie może ważyć zero funtów.

_b1 = 0,2001 . Oznacza to, że wzrost x o jedną jednostkę jest powiązany ze wzrostem y o 0,2001 jednostki. W tym przypadku wzrost wagi o jeden funt wiąże się ze wzrostem wzrostu o 0,2001 cala.

Jak korzystać z linii regresji metodą najmniejszych kwadratów

Korzystając z linii regresji metodą najmniejszych kwadratów, możemy odpowiedzieć na pytania takie jak:

Jakiego wzrostu powinniśmy się spodziewać w przypadku osoby ważącej 170 funtów?

Aby odpowiedzieć na to pytanie, możemy po prostu wstawić 170 do naszej linii regresji dla x i obliczyć y:

ŷ = 32,7830 + 0,2001(170) = 66,8 cala

Jakiego wzrostu powinniśmy się spodziewać w przypadku osoby ważącej 150 funtów?

Aby odpowiedzieć na to pytanie, możemy wstawić 150 do naszej linii regresji dla x i rozwiązać y:

ŷ = 32,7830 + 0,2001(150) = 62,798 cala

Uwaga: Używając równania regresji do odpowiedzi na tego typu pytania, pamiętaj, aby używać tylko wartości zmiennej predykcyjnej, które mieszczą się w zakresie zmiennej predykcyjnej w zbiorze danych. pochodzenia, którego użyliśmy do wygenerowania linii regresji metodą najmniejszych kwadratów. Na przykład wagi w naszym zestawie danych wahały się od 140 do 212 funtów. Dlatego sensowne jest odpowiadanie na pytania dotyczące oczekiwanego wzrostu, gdy waga wynosi od 140 do 212 funtów.

Współczynnik determinacji

Jednym ze sposobów pomiaru, jak dobrze linia regresji metodą najmniejszych kwadratów „pasuje” do danych, jest użycie współczynnika determinacji , oznaczonego R ² .

Współczynnik determinacji to proporcja wariancji zmiennej odpowiedzi, którą można wyjaśnić zmienną predykcyjną.

Współczynnik determinacji może zmieniać się od 0 do 1. Wartość 0 oznacza, że zmienna odpowiedzi nie może być w ogóle wyjaśniona zmienną predykcyjną. Wartość 1 wskazuje, że zmienna odpowiedzi może być doskonale i bezbłędnie wyjaśniona przez zmienną predykcyjną.

R2 ^pomiędzy 0 i 1 wskazuje, w jakim stopniu zmienna odpowiedzi może być wyjaśniona przez zmienną predykcyjną. Na przykład ^R2 równe 0,2 wskazuje, że 20% wariancji zmiennej odpowiedzi można wyjaśnić zmienną predykcyjną; ^R2 równe 0,77 wskazuje, że 77% wariancji zmiennej odpowiedzi można wyjaśnić zmienną predykcyjną.

Należy zauważyć, że w naszym poprzednim wyniku otrzymaliśmy R ² wynoszące 0,9311, co wskazuje, że 93,11% zmienności wzrostu można wyjaśnić zmienną predykcyjną masy ciała:

To mówi nam, że waga jest bardzo dobrym wskaźnikiem wzrostu.

Założenia regresji liniowej

Aby wyniki modelu regresji liniowej były ważne i wiarygodne, musimy sprawdzić, czy spełnione są następujące cztery założenia:

1. Zależność liniowa: Istnieje liniowa zależność pomiędzy zmienną niezależną x i zmienną zależną y.

2. Niezależność: Reszty są niezależne. W szczególności nie ma korelacji pomiędzy kolejnymi resztami w danych szeregów czasowych.

3. Homoscedastyczność: reszty mają stałą wariancję na każdym poziomie x.

4. Normalność: Reszty modelu mają rozkład normalny.

Jeśli jedno lub więcej z tych założeń nie zostanie spełnione, wyniki naszej regresji liniowej mogą być niewiarygodne lub nawet mylące.

W tym artykule znajdziesz wyjaśnienie każdego założenia, sposób ustalenia, czy założenie jest spełnione i co zrobić, jeśli założenie nie zostanie spełnione.