Regresja logarytmiczna

W tym artykule wyjaśniono, czym jest regresja logarytmiczna i jak jest wykonywana. Dodatkowo możesz zobaczyć przykład regresji logarytmicznej, aby w pełni zrozumieć tę koncepcję.

Co to jest regresja logarytmiczna?

Regresja logarytmiczna to model regresji, który w swoim równaniu uwzględnia logarytm. W szczególności w regresji logarytmicznej przyjmuje się logarytm zmiennej niezależnej. Zatem równanie modelu regresji logarytmicznej ma postać y=a+b·ln(x).

Regresja logarytmiczna jest bardzo przydatna do dopasowywania modelu regresji, gdy przykładowe dane tworzą krzywą logarytmiczną, dzięki czemu model regresji lepiej pasuje do przykładowych danych. Poniżej dowiemy się, kiedy należy wykonać regresję logarytmiczną.

Zatem regresja logarytmiczna jest rodzajem regresji nieliniowej, podobnie jak regresja wykładnicza i regresja wielomianowa.

Wzór regresji logarytmicznej

Model regresji logarytmicznej polega na przyjęciu logarytmu zmiennej niezależnej. Zatem wzór na równanie regresji logarytmicznej to y=a+b·ln(x).

Złoto:

• 

  jest zmienną zależną.

• 

  jest zmienną niezależną.

• 

  są współczynnikami regresji.

Zauważ, że y=a+b·ln(x) jest w rzeczywistości równaniem prostej, ale zamiast odnosić się do pierwotnych zmiennych x i y, odnosi się do zmiennych ln(x) i y.

Kiedy wykonać regresję logarytmiczną?

Regresję logarytmiczną musimy wykonać, gdy wykres przykładowych danych jest krzywą logarytmiczną, to znaczy, gdy wykres punktów jest podobny do wykresu funkcji logarytmicznej.

Spójrz na wykres rozrzutu poniżej. Do zbioru danych dopasowano model regresji liniowej. Jak widać linia nie jest złym przybliżeniem danych jednak jeśli się zachować ostrożność wartości rosną szybciej na początku wykresu niż na końcu więc linia nie do końca pokrywa się z obserwacjami .

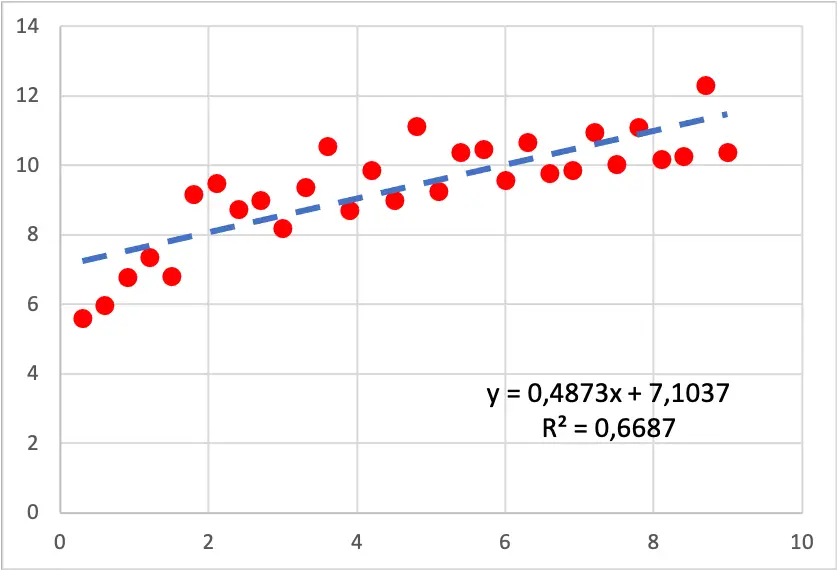
Warto więc spróbować stworzyć model regresji logarytmicznej, ponieważ wygląda na to, że dane podążają za krzywą logarytmiczną. Wynik uzyskany z modelu regresji logarytmicznej jest następujący:

Jak widać na poprzednim wykresie, powstały model regresji logarytmicznej lepiej pasuje do przykładowych danych. W rzeczywistości współczynnik determinacji wzrósł z 66,87% do 80,05%, dzięki czemu model może teraz lepiej wyjaśniać próbkę danych. Dlatego w tym przypadku lepiej zastosować regresję logistyczną, aby znaleźć równanie przybliżające wartość danych.

Inne rodzaje regresji nieliniowej

Trzy najczęstsze przypadki regresji nieliniowej to:

• Regresja logarytmiczna : przyjmuje się logarytm zmiennej niezależnej.
• Regresja wykładnicza : Zmienna niezależna jest wykładnikiem równania.
• Regresja wielomianowa : Równanie modelu regresji ma postać wielomianu.