Jak przeprowadzić regresję logistyczną w sas-ie

Regresja logistyczna to metoda, której możemy użyć do dopasowania modelu regresji, gdy zmienna odpowiedzi jest binarna.

Regresja logistyczna wykorzystuje metodę zwaną estymacją największej wiarygodności w celu znalezienia równania w następującej postaci:

log[p(X) / (1 _– p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

Złoto:

• X _j : j- ^ta zmienna predykcyjna
• β _j : estymacja współczynnika dla j ^-tej zmiennej predykcyjnej

Wzór po prawej stronie równania przewiduje logarytm szansy , że zmienna odpowiedzi przyjmie wartość 1.

Poniższy przykład pokazuje krok po kroku, jak dopasować model regresji logistycznej w SAS-ie.

Krok 1: Utwórz zbiór danych

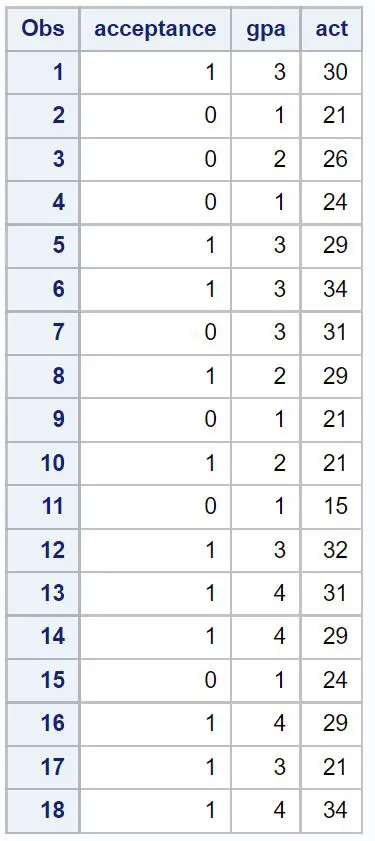
Najpierw utworzymy zbiór danych zawierający informacje o trzech zmiennych dla 18 uczniów:

• Przyjęcie na określoną uczelnię (1 = tak, 0 = nie)
• GPA (skala od 1 do 4)
• Wynik ACT (skala od 1 do 36)

 /*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines ;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run ;

/*view dataset*/
proc print data =my_data;

Krok 2: Dopasuj model regresji logistycznej

Następnie użyjemy logistyki proc , aby dopasować model regresji logistycznej, używając „akceptacji” jako zmiennej odpowiedzi oraz „gpa” i „działania” jako zmiennych predykcyjnych.

Uwaga : Aby SAS mógł przewidzieć prawdopodobieństwo, że zmienna odpowiedzi przyjmie wartość 1, należy określić zmniejszanie . Domyślnie SAS przewiduje prawdopodobieństwo, że zmienna odpowiedzi przyjmie wartość 0.

 /*fit logistic regression model*/
proc logistic data =my_data descending ;
  model acceptance = gpa act;
run ;

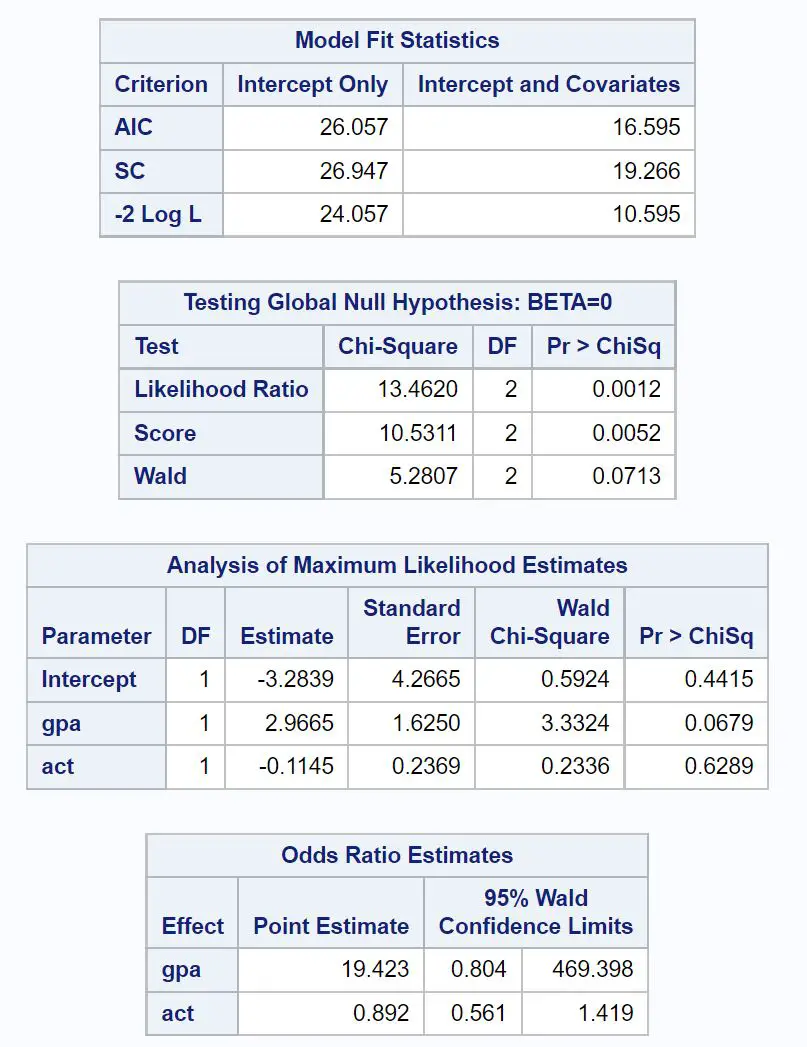
Pierwsza interesująca tabela nosi tytuł Statystyki dopasowania modelu .

Z tej tabeli możemy zobaczyć wartość AIC modelu, która okazuje się wynosić 16,595 . Im niższa wartość AIC, tym lepiej model jest w stanie dopasować dane.

Nie ma jednak progu określającego, co uważa się za „dobrą” wartość AIC . Zamiast tego używamy AIC do porównania dopasowania wielu modeli do tego samego zestawu danych. Model z najniższą wartością AIC jest powszechnie uważany za najlepszy.

Następna tabela nosi tytuł Testowanie globalnej hipotezy zerowej: BETA=0 .

Z tej tabeli możemy zobaczyć wartość chi-kwadrat współczynnika wiarygodności wynoszącą 13,4620 z odpowiadającą wartością p wynoszącą 0,0012 .

Ponieważ ta wartość p jest mniejsza niż 0,05, mówi nam to, że model regresji logistycznej jako całość jest istotny statystycznie.

Następnie możemy przeanalizować oszacowania współczynników w tabeli zatytułowanej Analiza szacunków maksymalnej wiarygodności .

Z tej tabeli możemy zobaczyć współczynniki gpa i act, które wskazują średnią zmianę logarytmu szans na przyjęcie na studia przy wzroście każdej zmiennej o jedną jednostkę.

Na przykład:

• Wzrost wartości GPA o jedną jednostkę wiąże się ze średnim wzrostem logarytmicznych szans na przyjęcie na studia o 2,9665 .
• Wzrost wyniku ACT o jedną jednostkę wiąże się ze średnim spadkiem logarytmicznych szans na przyjęcie na studia o średnio 0,1145 .

Odpowiednie wartości p w wyniku dają nam również wyobrażenie o tym, jak skuteczna jest każda zmienna predykcyjna w przewidywaniu prawdopodobieństwa akceptacji:

• Wartość P GPA: 0,0679
• ACT Wartość P: 0,6289

To mówi nam, że GPA wydaje się być statystycznie istotnym czynnikiem prognostycznym akceptacji uczelni, podczas gdy wynik ACT nie wydaje się statystycznie istotny.

Dodatkowe zasoby

Poniższe tutoriale wyjaśniają, jak dopasować inne modele regresji w SAS-ie:

Jak wykonać prostą regresję liniową w SAS-ie
Jak wykonać wielokrotną regresję liniową w SAS-ie