Regresja przez pochodzenie: definicja i przykład

Prosta regresja liniowa to metoda, którą można zastosować do ilościowego określenia związku między jedną lub większą liczbą zmiennych predykcyjnych azmienną odpowiedzi .

Prosty model regresji liniowej przyjmuje następującą postać:

y = β ₀ + β ₁ x

Złoto:

• y : Wartość zmiennej odpowiedzi
• β ₀ : Wartość zmiennej odpowiedzi, gdy x = 0 (nazywana składnikiem „wycięcia”)
• β ₁ : Średni wzrost zmiennej odpowiedzi powiązany ze wzrostem x o jedną jednostkę
• x : Wartość zmiennej predykcyjnej

Zmodyfikowana wersja tego modelu znana jest jako regresja przez początek , która wymusza, aby y było równe 0, gdy x jest równe 0.

Ten typ modelu przyjmuje następującą postać:

y = _β1x

Należy zauważyć, że człon wyrazu wolnego został całkowicie usunięty z modelu.

Model ten jest czasami używany, gdy badacze wiedzą, że zmienna odpowiedzi musi wynosić zero, gdy zmienna predykcyjna wynosi zero.

W świecie rzeczywistym tego typu model najczęściej wykorzystuje się w badaniach leśnych czy ekologicznych .

Na przykład badacze mogą wykorzystać obwód drzewa do przewidywania wysokości drzewa. Jeśli dane drzewo ma zerowy obwód, musi mieć zerową wysokość.

Zatem dopasowując model regresji do tych danych, nie miałoby sensu, aby pierwotny składnik był różny od zera.

Poniższy przykład pokazuje różnicę między dopasowaniem zwykłego prostego modelu regresji liniowej a modelem, który implementuje regresję poprzez początek.

Przykład: regresja przez początek

Załóżmy, że biolog chce dopasować model regresji, wykorzystując obwód drzewa do przewidywania wysokości drzewa. Wychodzi i zbiera następujące pomiary dla próbki 15 drzew:

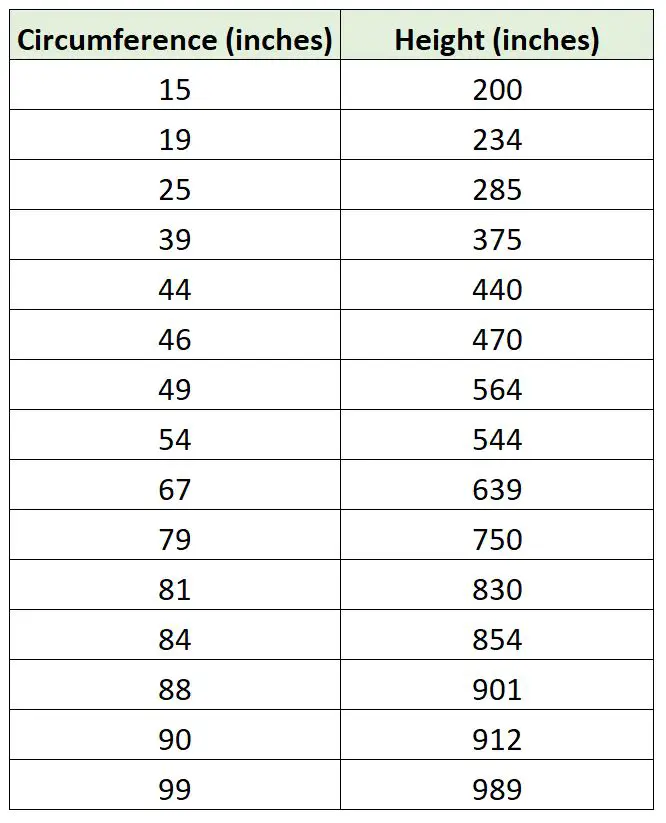
Możemy użyć następującego kodu w języku R, aby dopasować prosty model regresji liniowej do modelu regresji, który nie wykorzystuje punktów przecięcia, i wykreślić dwie linie regresji:

 #create data frame
df <- data. frame (circ=c(15, 19, 25, 39, 44, 46, 49, 54, 67, 79, 81, 84, 88, 90, 99),
                 height=c(200, 234, 285, 375, 440, 470, 564, 544, 639, 750, 830, 854,
                          901, 912, 989))

#fit a simple linear regression model
model <- lm(height ~ circ, data = df)

#fit regression through the origin
model_origin <- lm(height ~ 0 + ., data = df)

#create scatterplot
plot(df$circ, df$height, xlab=' Circumference ', ylab=' Height ',
     cex= 1.5 , pch= 16 , ylim=c(0.1000), xlim=c(0.100))

#add the fitted regression lines to the scatterplot
abline(model, col=' blue ', lwd= 2 )
abline(model_origin, lty=' dashed ', col=' red ', lwd= 2 )

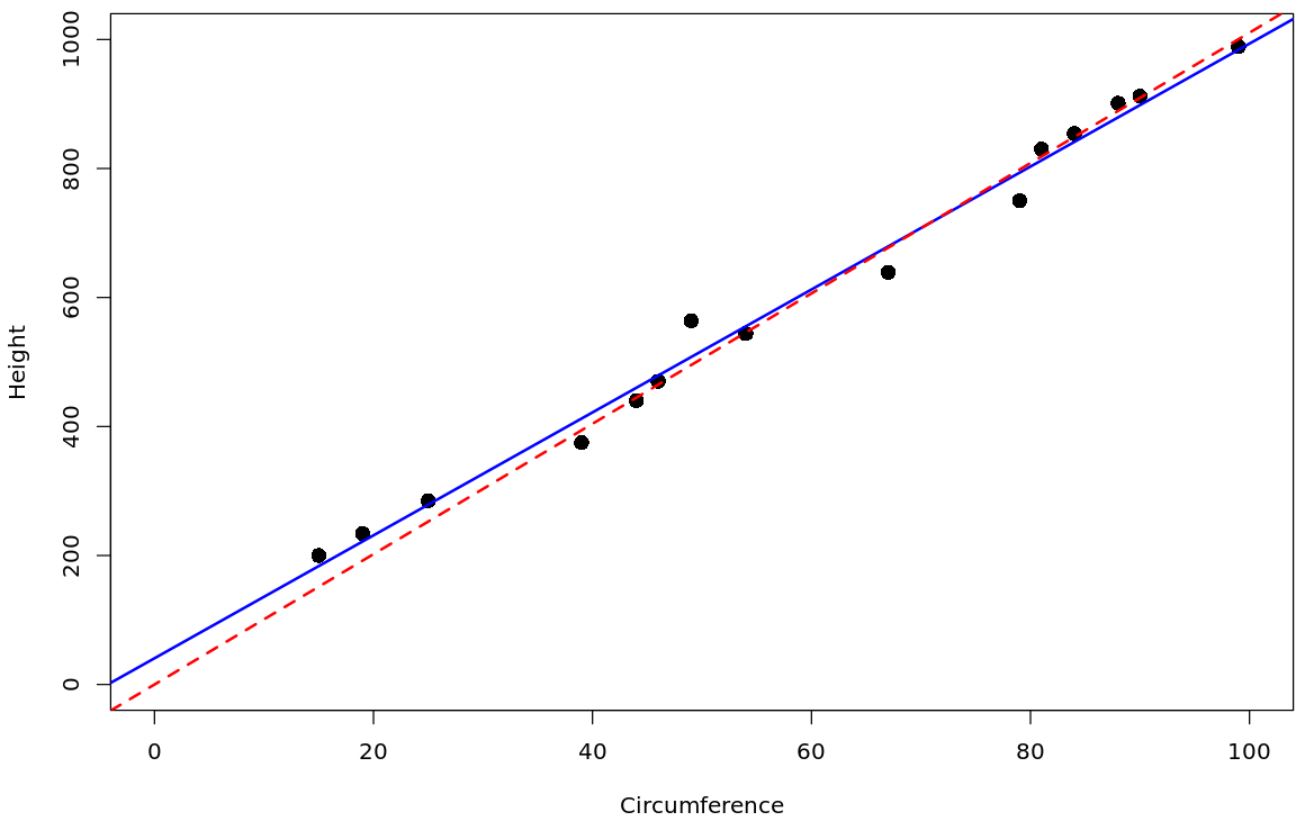
Czerwona linia przerywana przedstawia model regresji przechodzący przez początek, a niebieska linia ciągła przedstawia zwykły prosty model regresji liniowej.

Możemy użyć następującego kodu w R, aby uzyskać oszacowania współczynników dla każdego modelu:

 #display coefficients for simple linear regression model
coef(model)

(Intercept) circ 
  40.696971 9.529631 

#display coefficients for regression model through the origin
coef(model_origin)

    circ 
10.10574 

Dopasowane równanie prostego modelu regresji liniowej wygląda następująco:

Wysokość = 40,6969 + 9,5296 (obwód)

Dopasowane równanie modelu regresji poprzez początek to:

Wysokość = 10,1057 (obwód)

Należy zauważyć, że szacunki współczynników dla zmiennej obwodu są nieco inne.

Środki ostrożności dotyczące stosowania regresji poprzez początek

Przed użyciem regresji przecięcia należy mieć całkowitą pewność, że wartość 0 dla zmiennej predykcyjnej implikuje wartość 0 dla zmiennej odpowiedzi. W wielu scenariuszach prawie niemożliwe jest, aby mieć pewność.

A jeśli użyjesz regresji poprzez początek, aby zachować pewien stopień swobody w szacowaniu pochodzenia, rzadko robi to znaczącą różnicę, jeśli wielkość próbki jest wystarczająco duża.

Jeśli zdecydujesz się zastosować regresję poprzez początek, pamiętaj o przedstawieniu swojego rozumowania w końcowej analizie lub raporcie.

Dodatkowe zasoby

Poniższe samouczki zawierają dodatkowe informacje na temat regresji liniowej:

Wprowadzenie do prostej regresji liniowej
Wprowadzenie do wielokrotnej regresji liniowej
Jak czytać i interpretować tabelę regresji