Jak wykonać regresję wielomianową za pomocą scikit-learn

Regresja wielomianowa to technika, którą możemy zastosować, gdy związek między zmienną predykcyjną a zmienną odpowiedzi jest nieliniowy.

Ten typ regresji przyjmuje postać:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _godz

gdzie h jest „stopniem” wielomianu.

Poniższy przykład pokazuje krok po kroku, jak przeprowadzić regresję wielomianową w Pythonie za pomocą sklearn.

Krok 1: Utwórz dane

Najpierw utwórzmy dwie tablice NumPy do przechowywania wartości predyktora i zmiennej odpowiedzi:

 import matplotlib. pyplot as plt
import numpy as np

#define predictor and response variables
x = np. array ([2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12])
y = np. array ([18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29])

#create scatterplot to visualize relationship between x and y
plt. scatter (x,y)

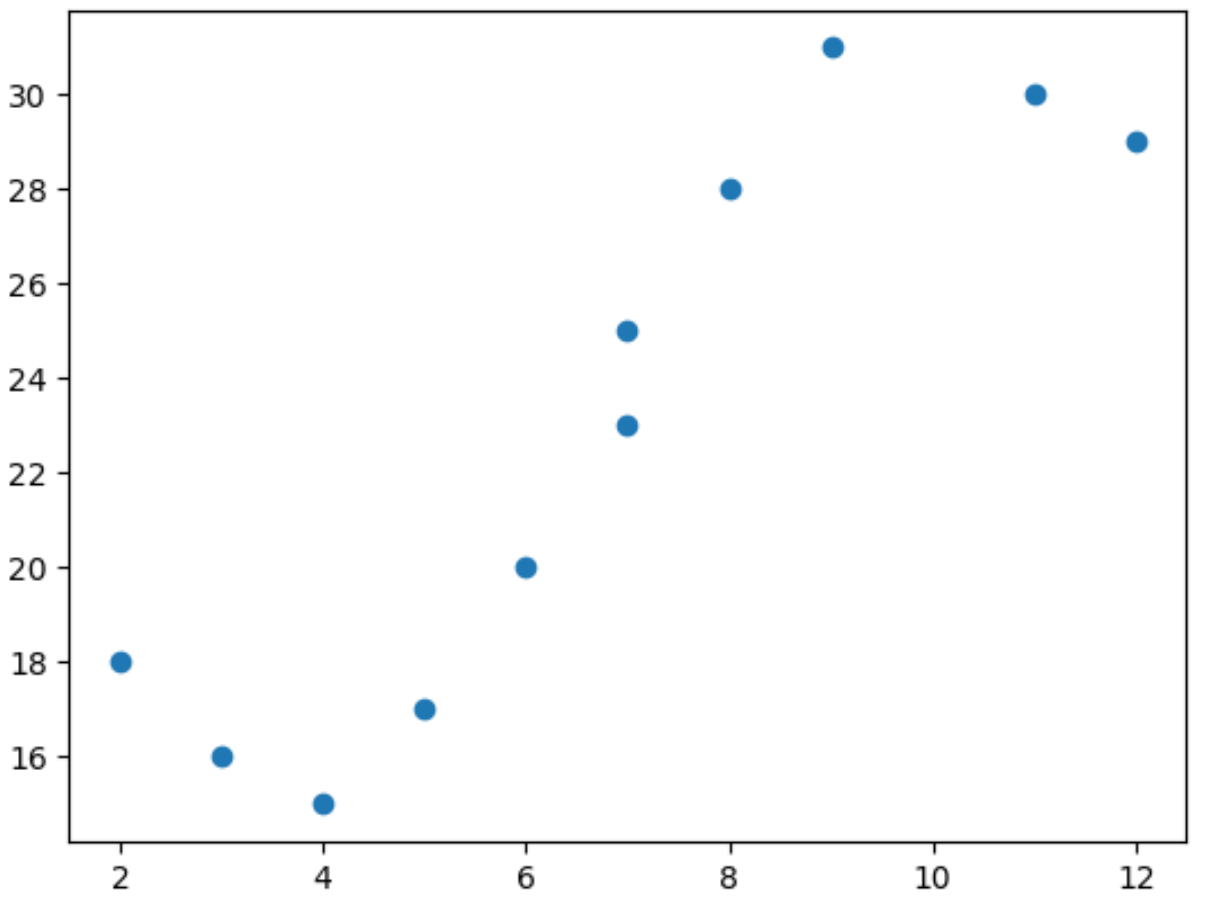
Z wykresu rozrzutu widzimy, że zależność między x i y nie jest liniowa.

Dlatego dobrym pomysłem jest dopasowanie do danych modelu regresji wielomianowej, aby uchwycić nieliniową zależność między dwiema zmiennymi.

Krok 2: Dopasuj model regresji wielomianowej

Poniższy kod pokazuje, jak używać funkcji sklearn w celu dopasowania modelu regresji wielomianowej trzeciego stopnia do tego zbioru danych:

 from sklearn. preprocessing import PolynomialFeatures
from sklearn. linear_model import LinearRegression

#specify degree of 3 for polynomial regression model
#include bias=False means don't force y-intercept to equal zero
poly = PolynomialFeatures(degree= 3 , include_bias= False )

#reshape data to work properly with sklearn
poly_features = poly. fit_transform ( x.reshape (-1, 1))

#fit polynomial regression model
poly_reg_model = LinearRegression()
poly_reg_model. fit (poly_features,y)

#display model coefficients
print (poly_reg_model. intercept_ , poly_reg_model. coef_ )

33.62640037532282 [-11.83877127 2.25592957 -0.10889554]

Korzystając ze współczynników modelu pokazanych w ostatnim wierszu, możemy zapisać dopasowane równanie regresji wielomianowej w następujący sposób:

y = -0,109x ³ + 2,256x ² – 11,839x + 33,626

Równanie to można wykorzystać do znalezienia oczekiwanej wartości zmiennej odpowiedzi, przy danej wartości przewidywanej zmiennej.

Na przykład, jeśli x wynosi 4, oczekiwana wartość zmiennej odpowiedzi y wyniesie 15,39:

y = -0,109(4) ³ + 2,256(4) ² – 11,839(4) + 33,626= 15,39

Uwaga : Aby dopasować model regresji wielomianowej o innym stopniu, wystarczy zmienić wartość argumentu stopnia w funkcji PolynomialFeatures() .

Krok 3: Wizualizuj model regresji wielomianowej

Na koniec możemy utworzyć prosty wykres wizualizujący model regresji wielomianowej dopasowany do oryginalnych punktów danych:

 #use model to make predictions on response variable
y_predicted = poly_reg_model. predict (poly_features)

#create scatterplot of x vs. y
plt. scatter (x,y)

#add line to show fitted polynomial regression model
plt. plot (x,y_predicted,color=' purple ')

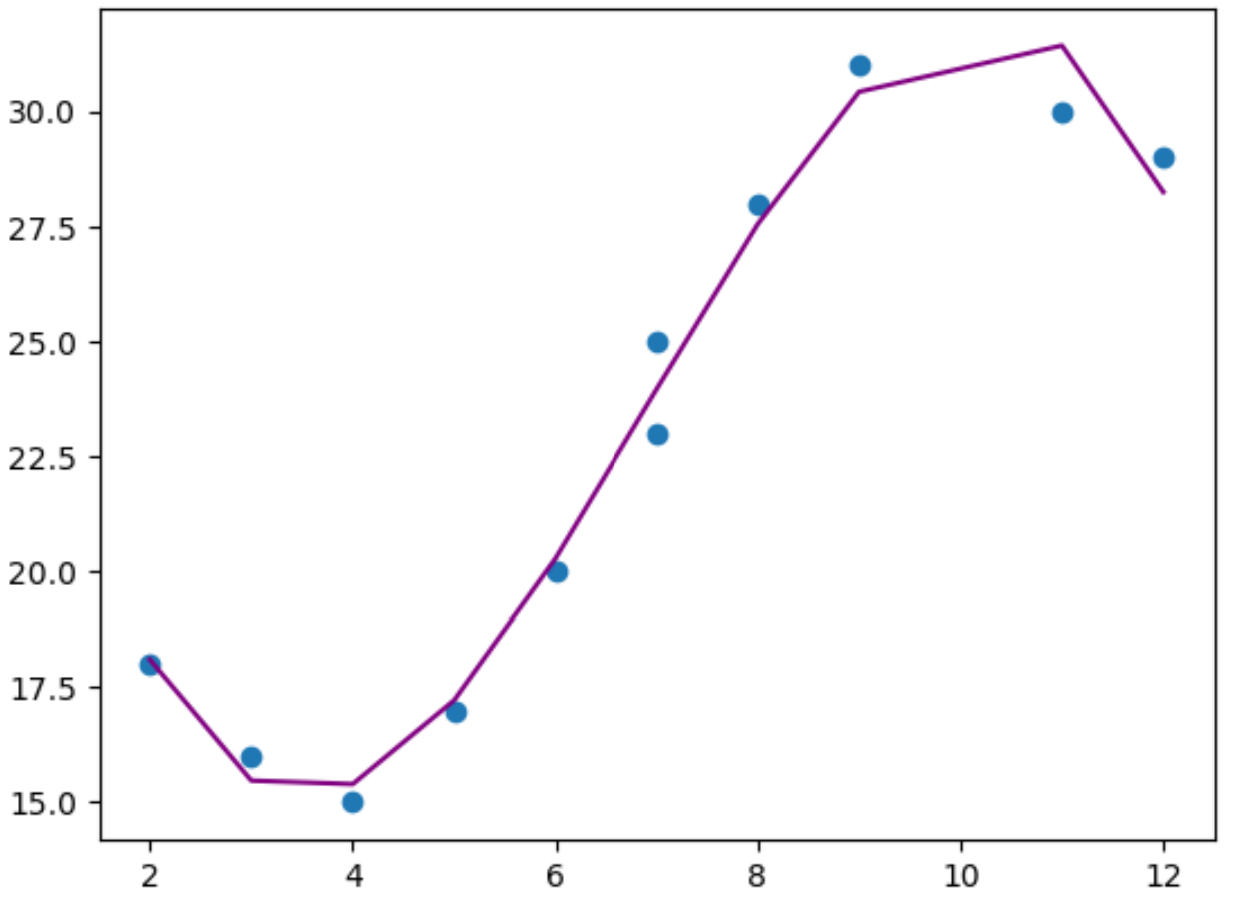
Z wykresu widać, że model regresji wielomianowej wydaje się dobrze pasować do danych, bez nadmiernego dopasowania .

Uwaga : Pełną dokumentację funkcji sklearn PolynomialFeatures() można znaleźć tutaj .

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania za pomocą sklearn:

Jak wyodrębnić współczynniki regresji z pliku sklearn
Jak obliczyć zrównoważoną precyzję za pomocą sklearn
Jak interpretować raport klasyfikacyjny w Sklearn