Co to są reszty standaryzowane?

Reszta to różnica między wartością obserwowaną a wartością przewidywaną w modelu regresji .

Oblicza się go w następujący sposób:

Wartość rezydualna = Wartość obserwowana – Wartość przewidywana

Jeśli wykreślimy zaobserwowane wartości i nałożymy dopasowaną linię regresji, resztą dla każdej obserwacji będzie pionowa odległość między obserwacją a linią regresji:

Jeden z typów reszt, którego często używamy do identyfikacji wartości odstających w modelu regresji, nazywany jest resztą standaryzowaną .

Oblicza się go w następujący sposób:

r _ja = mi _ja / s(e _ja ) = mi _ja / RSE√ 1-h _ii

Złoto:

• e _i : i- ^ta reszta
• RSE: resztkowy błąd standardowy modelu
• h _ii : Powstanie i ^-tej obserwacji

W praktyce często za wartość odstającą uznajemy każdą standaryzowaną resztę, której wartość bezwzględna jest większa niż 3.

Nie musi to koniecznie oznaczać, że usuniemy te obserwacje z modelu, ale powinniśmy przynajmniej je dokładniej przestudiować, aby sprawdzić, czy nie są one wynikiem błędu we wprowadzaniu danych lub innego dziwnego zdarzenia.

Uwaga: Czasami pozostałości standaryzowane nazywane są także „pozostałościami badanymi wewnętrznie”.

Przykład: Jak obliczyć reszty standaryzowane

Załóżmy, że mamy następujący zbiór danych zawierający łącznie 12 obserwacji:

Jeśli użyjemy oprogramowania statystycznego (takiego jak R , Excel , Python , Stata itp.), aby dopasować linię regresji liniowej do tego zbioru danych, odkryjemy, że linia najlepszego dopasowania okaże się:

y = 29,63 + 0,7553x

Korzystając z tej linii, możemy obliczyć przewidywaną wartość dla każdej wartości Y w oparciu o wartość X. Na przykład przewidywana wartość pierwszej obserwacji będzie wynosić:

y = 29,63 + 0,7553*(8) = 35,67

Następnie możemy obliczyć resztę tej obserwacji w następujący sposób:

Wartość rezydualna = Wartość obserwowana – Wartość przewidywana = 41 – 35,67 = 5,33

Możemy powtórzyć ten proces, aby znaleźć resztę dla każdej obserwacji:

Możemy również użyć oprogramowania statystycznego, aby stwierdzić, że resztkowy błąd standardowy modelu wynosi 4,44 .

I chociaż wykracza to poza zakres tego samouczka, możemy użyć oprogramowania, aby znaleźć statystykę dźwigni (h _ii ) dla każdej obserwacji:

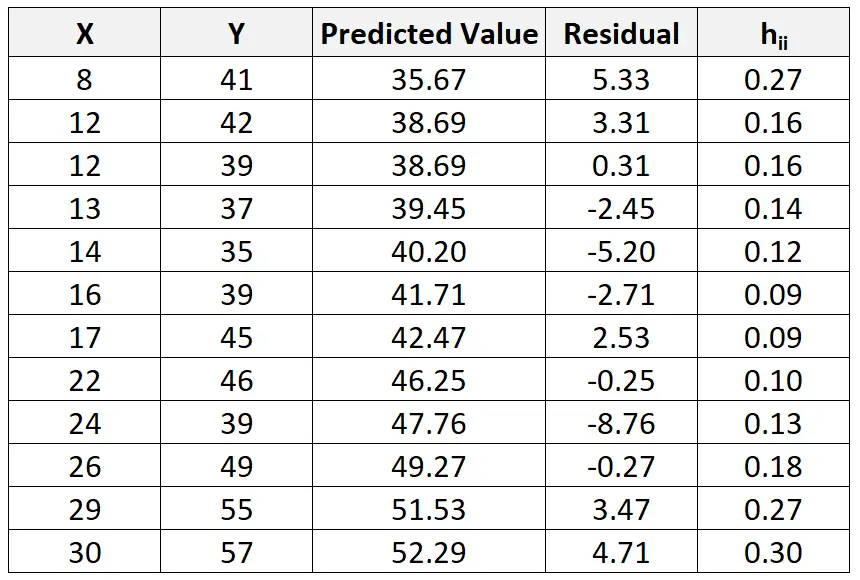
Następnie możemy użyć następującego wzoru do obliczenia reszty standaryzowanej dla każdej obserwacji:

r _ja = mi _ja / RSE√ 1-h _ii

Na przykład resztę standaryzowaną dla pierwszej obserwacji oblicza się w następujący sposób:

r _ja = 5,33 / 4,44√ 1-0,27 = 1,404

Możemy powtórzyć ten proces, aby znaleźć resztę standaryzowaną dla każdej obserwacji:

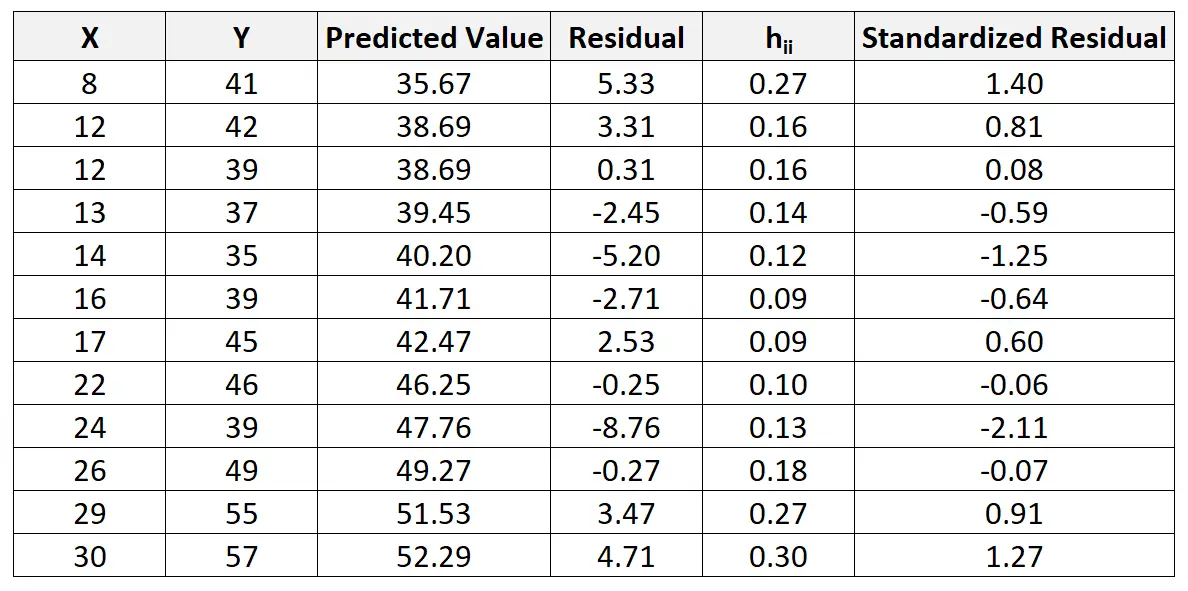
Następnie możemy utworzyć szybki wykres rozrzutu wartości predykcyjnych względem reszt standaryzowanych, aby wizualnie sprawdzić, czy którakolwiek z reszt standaryzowanych przekracza próg wartości bezwzględnej wynoszący 3:

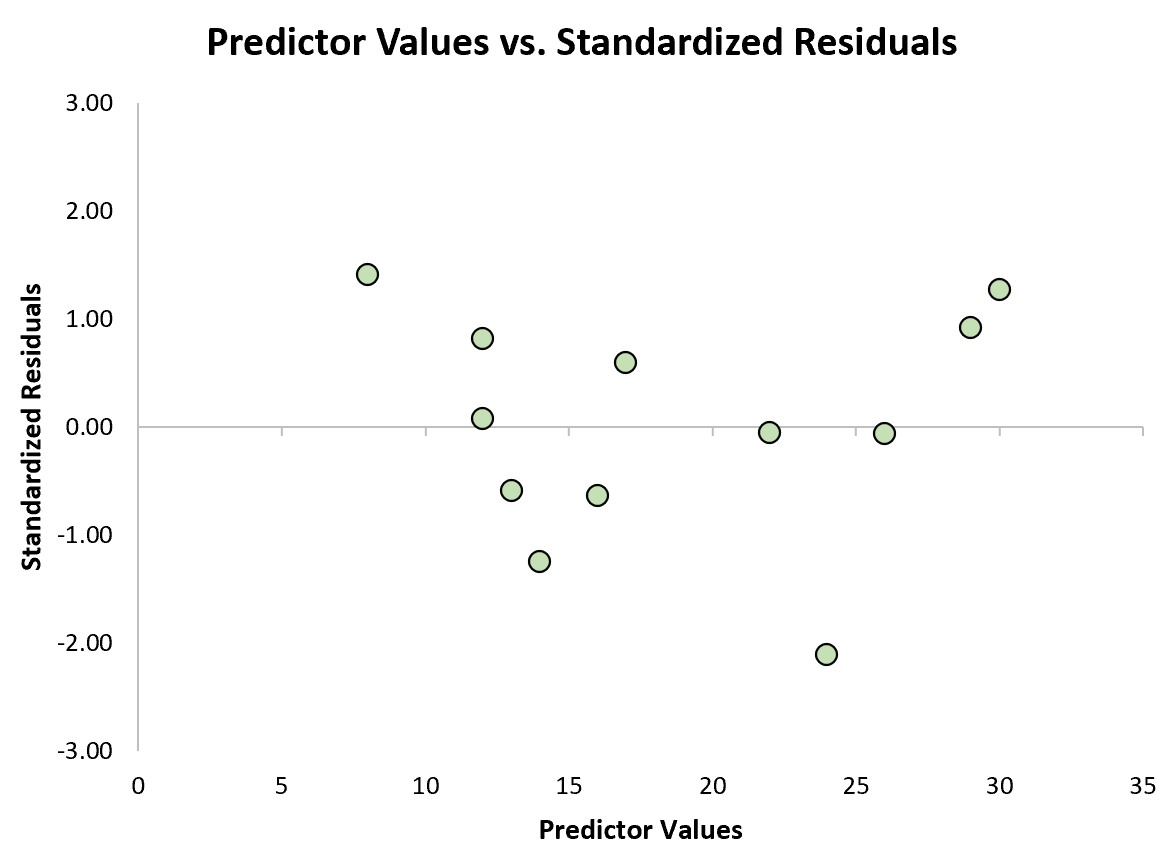
Z wykresu widać, że żadna ze standaryzowanych reszt nie przekracza wartości bezwzględnej 3. Zatem żadna z obserwacji nie wydaje się być wartością odstającą.

Należy zauważyć, że w niektórych przypadkach badacze uważają obserwacje, których reszty standaryzowane przekraczają wartość bezwzględną 2, za obserwacje odstające.

To od Ciebie zależy, w zależności od dziedziny, w której pracujesz i konkretnego problemu, nad którym pracujesz, czy chcesz zastosować wartość bezwzględną 2 czy 3 jako próg dla wartości odstających.

Dodatkowe zasoby

Poniższe samouczki dostarczają dodatkowych informacji na temat reszt standaryzowanych:

Czym są reszty w statystyce?
Jak obliczyć reszty standaryzowane w programie Excel
Jak obliczyć reszty standaryzowane w R
Jak obliczyć reszty standaryzowane w Pythonie