Typy średnie (statystyki)

Przez Benjamin Anderson 6 sierpnia, 2023 Statystyka 0 komentarzy

Tutaj wyjaśniamy, jakie są wszystkie rodzaje średnich w statystykach i jak są obliczane. Znajdziesz tu przepis na każdy rodzaj pończoch oraz przykłady.

Zanim jednak zobaczymy, jakie są rodzaje średniej, musimy logicznie wiedzieć, czym jest średnia w statystyce. Dlatego przed kontynuowaniem zalecamy skorzystanie z poniższego łącza.

➤ Zobacz: Jaka jest średnia (statystyki)?

Jakie są rodzaje średnich w statystyce?

W statystyce rodzaje średnich to:

Średnia arytmetyczna
Średnia ważona
Środki geometryczne
pierwiastek oznacza kwadrat
znaczenie harmoniczne
uogólniona średnia
uogólniona średnia f
przycięte środki
średnia międzykwartylowa
średnia funkcji

Następnie wyjaśnimy, jak obliczać wszystkie rodzaje średnich w statystyce. Pięć najczęściej używanych typów średnich to średnia arytmetyczna, średnia ważona, średnia geometryczna, średnia kwadratowa i średnia harmoniczna. Zajmiemy się więc bardziej szczegółowo tymi pięcioma głównymi typami mediów.

Średnia arytmetyczna

Średnią arytmetyczną oblicza się, dodając wszystkie wartości, a następnie dzieląc przez całkowitą liczbę punktów danych.

Wzór na średnią arytmetyczną jest zatem następujący:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+\dots+x_N}{N}$

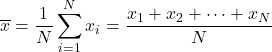
Średnia arytmetyczna jest również nazywana średnią arytmetyczną .

Średnia arytmetyczna jest prawdopodobnie najczęściej używanym rodzajem średniej w statystyce.

Aby zobaczyć przykładowy sposób uzyskiwania tego typu średniej, obliczymy średnią arytmetyczną następujących danych:

$4\quad 7\quad 10\quad 1\quad 8\quad9$

Aby obliczyć średnią arytmetyczną, wystarczy dodać wszystkie dane statystyczne i podzielić przez całkowitą liczbę danych, która wynosi 6:

$\overline{x}=\cfrac{4+7+10+1+8+9}{6}=6,5$

Średnia ważona

Aby obliczyć średnią ważoną, należy najpierw pomnożyć każdą dane statystyczną przez jej wagę (lub wagę), następnie dodać wszystkie iloczyny, a na koniec podzielić sumę ważoną przez sumę wszystkich wag.

Wzór na średnią ważoną wygląda zatem następująco:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+\dots x_N\cdot w_N}{w_1+w_2+\dosts +w_N}$

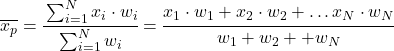
Gdzie x _i jest wartością statystyczną, a w _i odpowiadającą jej wagą.

Średnia ważona jest trudniejsza do zrozumienia, dlatego zalecamy zapoznanie się z poniższym przykładem, który wyjaśnia krok po kroku, jak jest obliczana:

➤ Zobacz: Przykład średniej ważonej

Środki geometryczne

Średnia geometryczna zbioru danych statystycznych jest równa n-temu pierwiastkowi iloczynu wszystkich wartości.

Ten typ średniej jest używany w finansach przedsiębiorstw do obliczania stóp zwrotu, średnich procentowych i odsetek składanych.

Przepis na tego typu przechowywanie jest dość skomplikowany. W rzeczywistości nie można obliczyć średniej geometrycznej wszystkich zbiorów statystycznych, ale czasami nie można wyznaczyć tego rodzaju średniej. Dlatego zalecamy zapoznanie się ze wszystkimi wyjątkami wyjaśnionymi w poniższym linku:

➤ Zobacz: wzór na średnią geometryczną

pierwiastek oznacza kwadrat

Średnia kwadratowa jest równa pierwiastkowi kwadratowemu średniej arytmetycznej kwadratów danych.

Wzór średniokwadratowy wygląda zatem następująco:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

Ten typ średniej nazywany jest również średnią kwadratową , średnią kwadratową lub RMS .

Zwróćmy tylko uwagę, że średnia sześcienna również istnieje, ale jest używana w bardzo szczególnych przypadkach.

Uśrednianie kwadratowe ma zalety i wady, jest na przykład szczególnie przydatne, gdy zmienna statystyczna przyjmuje wartości dodatnie i ujemne, ponieważ podnosząc do kwadratu każdą porcję danych, wszystkie wartości stają się dodatnie. Więcej funkcji tego typu multimediów można zobaczyć, klikając poniższy link:

➤ Zobacz: zalety i wady średniej kwadratowej

znaczenie harmoniczne

Średnią harmoniczną oblicza się, dzieląc całkowitą liczbę danych statystycznych przez sumę odwrotności każdej wartości.

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}$

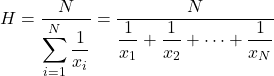
Średnia harmoniczna służy do obliczania średnich prędkości, czasów lub wykonywania obliczeń elektronicznych. Cecha ta odróżnia średnią harmoniczną od innych typów średnich, często stosowanych przy obliczaniu średnich cen lub wartości procentowych.

Przykłady obliczania tego typu średniej możesz zobaczyć na poniższej stronie:

➤ Zobacz: przykłady znaczenia harmonicznego

Inne rodzaje pończoch

W tej sekcji zobaczymy przepisy na inne rodzaje pończoch. Nie będziemy szczegółowo omawiać każdego rodzaju pończoch, ponieważ nie są one powszechnie stosowane, ale warto wiedzieć, że istnieją inne rodzaje pończoch.

Średnia uogólniona jest mieszaniną typów średnich przedstawionych powyżej i jest obliczana przy użyciu następującego wzoru:

$\displaystyle\overline{x}(m) = \left ( \frac{1}{N}\cdot\sum_{i=1}^N{x_i^m} \right ) ^{1/m}$

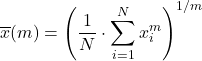
Niech f będzie funkcją iniekcyjną i monotoniczną, a następnie uogólnioną średnią f zdefiniowaną jako:

$\displaystyle\overline{x} = f^{-1}\left({\frac{1}{N}\cdot\sum_{i=1}^N{f(x_i)}}\right)$

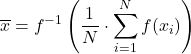
Średnia obcięta polega na obliczeniu średniej arytmetycznej po odjęciu procentu obserwacji na górnym i dolnym końcu próbki. Ten sam procent należy odrzucić na obu końcach.

Aby obliczyć średnią międzykwartylową , zwaną także średnią międzykwartylową, najpierw odrzuca się dane z pierwszego i czwartego kwartyla, a następnie oblicza się średnią arytmetyczną jedynie drugiego i trzeciego kwartyla próbki. Wzór na tego typu średnią wygląda zatem następująco:

$\displaystyle\overline{x}={2 \over n} \sum_{i=\frac{n}{4}+1}^{\frac{3n}{4}}{x_i}$

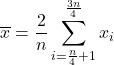
Na koniec można także znaleźć średnią funkcji . Wartość średnią funkcji ciągłej na przedziale domkniętym [a,b] oblicza się ze wzoru:

$\displaystyle\overline{f}=\frac{1}{b-a} \int_a^b f(t) dt$

Próba i średnia populacji

Na koniec zobaczymy, jaka jest różnica między średnią próbki a średnią populacji, dwoma rodzajami średnich, które często są mylone.

Średnia próbki to średnia obliczona na podstawie wartości próbki statystycznej, to znaczy jest obliczana na części wszystkich wartości zmiennej.

Średnia populacji to średnia obliczona dla populacji statystycznej, to znaczy dla wszystkich wartości zmiennej. Dlatego średnia populacji pokrywa się z matematycznym oczekiwaniem zmiennej.

Średnią próbki można uznać za praktycznie równą średniej populacji, jeśli znana jest wystarczająco duża ilość danych. Jednak wartość średniej populacji jest bardzo trudna do uzyskania, ponieważ w rzeczywistości wszystkie wartości rozkładu są rzadko znane.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej