Wprowadzenie do jednolitej dystrybucji

Rozkład równomierny to rozkład prawdopodobieństwa, w którym każda wartość w przedziale od a do b ma to samo prawdopodobieństwo wystąpienia.

Jeśli zmienna losowa X ma rozkład równomierny, wówczas prawdopodobieństwo, że X przyjmie wartość z zakresu od x ₁ do x ₂ , można obliczyć za pomocą następującego wzoru:

P(x ₁ < X < x ₂ ) = (x ₂ – x ₁ ) / (b – a)

Złoto:

• x ₁ : dolna wartość odsetek
• x ₂ : górna wartość zainteresowania
• a: minimalna możliwa wartość
• b: maksymalna możliwa wartość

Załóżmy na przykład, że waga delfinów jest równomiernie rozłożona między 100 a 150 funtów.

Jeśli wybierzemy losowo delfina, możemy skorzystać z powyższego wzoru, aby określić prawdopodobieństwo, że wybrany delfin waży od 120 do 130 funtów:

• P(120 < X < 130) = (130 – 120) / (150 – 100)
• P(120 < X < 130) = 10/50
• P(120 < X < 130) = 0,2

Prawdopodobieństwo, że wybrany delfin waży od 120 do 130 funtów, wynosi 0,2 .

Wizualizuj równomierną dystrybucję

Jeśli utworzymy wykres gęstości w celu wizualizacji równomiernego rozkładu, będzie on wyglądał następująco:

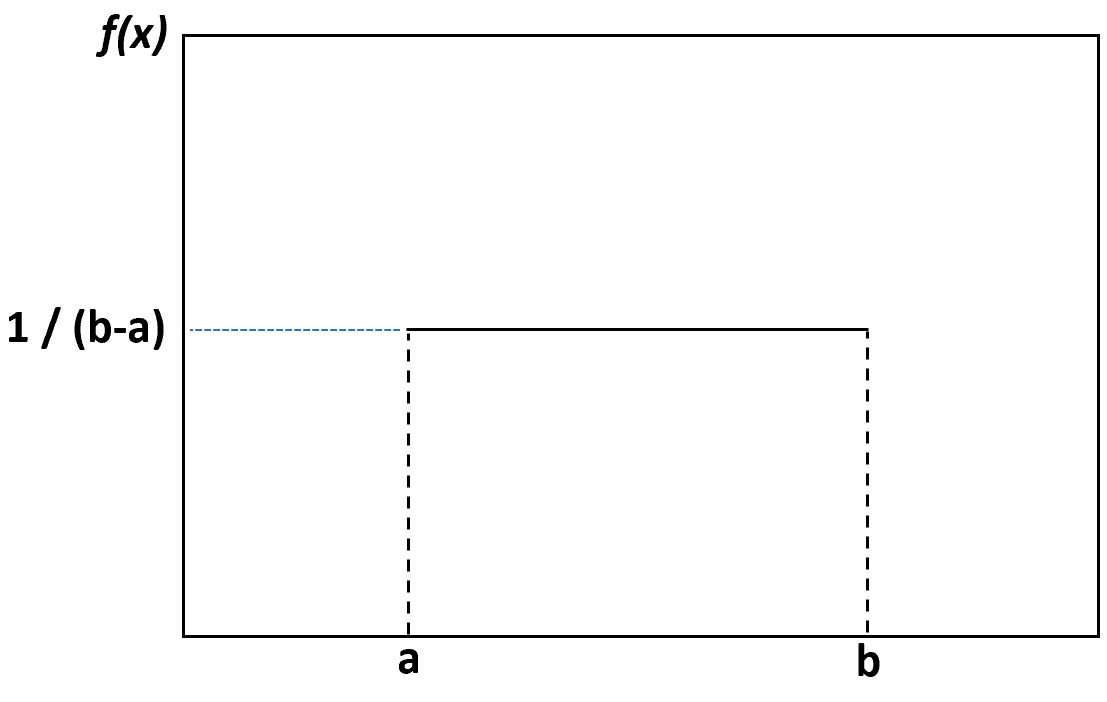
Każda wartość pomiędzy dolną granicą a i górną granicą b ma takie samo prawdopodobieństwo wystąpienia, a każda wartość poza tymi granicami ma prawdopodobieństwo zera.

Na przykład w naszym poprzednim przykładzie powiedzieliśmy, że waga delfinów jest równomiernie rozłożona w przedziale od 100 do 150 funtów. Oto jak zwizualizować tę dystrybucję:

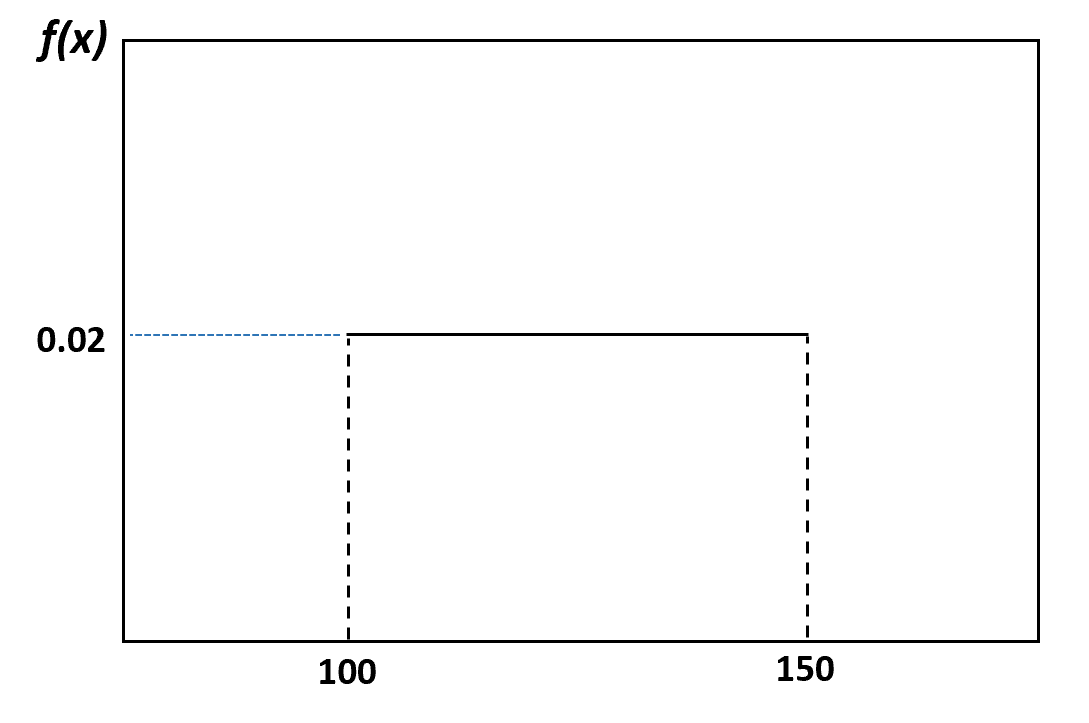
Prawdopodobieństwo, że losowo wybrany delfin waży od 120 do 130 funtów, można zwizualizować w następujący sposób:

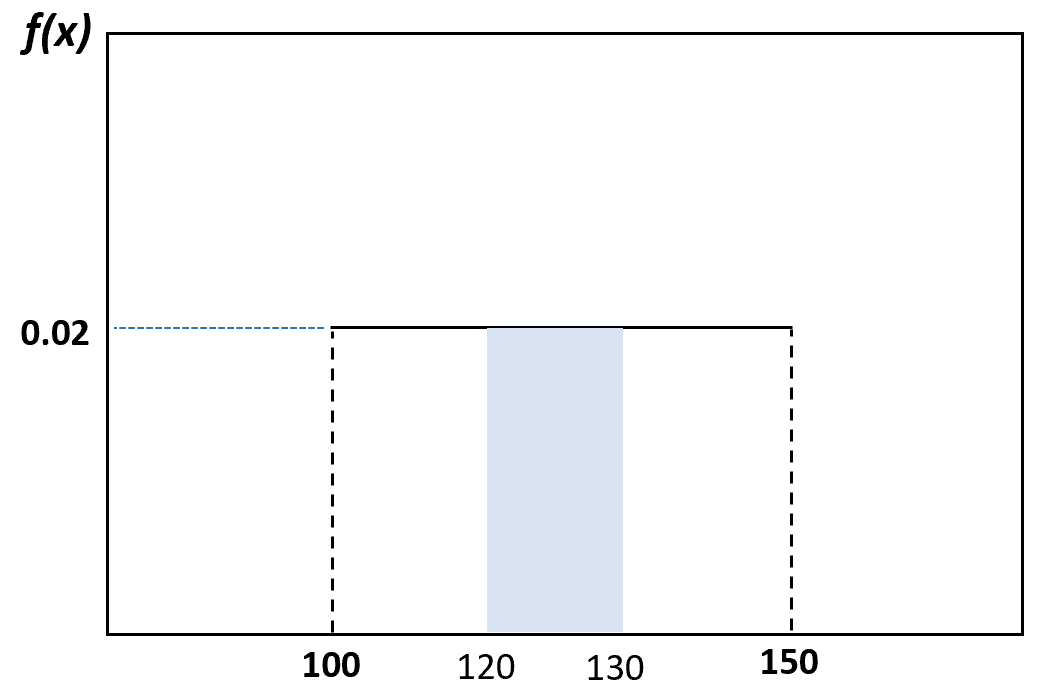
Właściwości rozkładu równomiernego

Rozkład równomierny ma następujące właściwości:

• Średnia: (a + b) / 2
• Mediana: (a + b) / 2
• Odchylenie standardowe: √ (b – a) ² / 12
• Różnica: (b – a) ² / 12

Załóżmy na przykład, że waga delfinów jest równomiernie rozłożona między 100 a 150 funtów.

Możemy obliczyć następujące właściwości tego rozkładu:

• Średnia waga: (a + b) / 2 = (150 + 100) / 2 = 125
• Mediana wagi: (a + b) / 2 = (150 + 100) / 2 = 125
• Odchylenie standardowe wagi: √ (150 – 100) ² / 12 = 14,43
• Zmiana masy: (150 – 100) ² / 12 = 208,33

Problemy z jednolitymi praktykami dystrybucyjnymi

Skorzystaj z poniższych problemów praktycznych, aby sprawdzić swoją wiedzę na temat rozkładu jednostajnego.

Pytanie 1: Autobus podjeżdża na przystanek co 20 minut. Jeśli dotrzesz na przystanek autobusowy, jakie jest prawdopodobieństwo, że autobus przyjedzie za 8 minut lub szybciej?

Rozwiązanie 1: Minimalny czas oczekiwania wynosi 0 minut, a maksymalny czas oczekiwania to 20 minut. Dolna wartość odsetek wynosi 0 minut, a górna wartość odsetek wynosi 8 minut.

Zatem prawdopodobieństwo obliczymy w następujący sposób:

P(0 < X < 8) = (8-0) / (20-0) = 8/20 = 0,4 .

Pytanie 2: Czas trwania meczu NBA rozkłada się równomiernie i wynosi od 120 do 170 minut. Jakie jest prawdopodobieństwo, że losowo wybrany mecz NBA będzie trwał dłużej niż 155 minut?

Rozwiązanie 2: Minimalny czas trwania wynosi 120 minut, a maksymalny czas trwania to 170 minut. Dolna wartość odsetek wynosi 155 minut, a górna wartość odsetek wynosi 170 minut.

Zatem prawdopodobieństwo obliczymy w następujący sposób:

P(155 < X < 170) = (170-155) / (170-120) = 15/50 = 0,3 .

Pytanie 3: Masa określonego gatunku żaby rozkłada się równomiernie pomiędzy 15 a 25 gramów. Jeśli wybierzesz losowo żabę, jakie jest prawdopodobieństwo, że waży ona od 17 do 19 gramów?

Rozwiązanie 3: Minimalna waga to 15 gramów, a maksymalna waga to 25 gramów. Dolna wartość odsetek wynosi 17 gramów, a górna wartość odsetek wynosi 19 gramów.

Zatem prawdopodobieństwo obliczymy w następujący sposób:

P(17 < X < 19) = (19-17) / (25-15) = 2/10 = 0,2 .

Uwaga: możemy użyć kalkulatora rozkładu jednolitego, aby sprawdzić nasze odpowiedzi na każdy z tych problemów.