Rozkład chi-kwadrat

Przez Benjamin Anderson 4 sierpnia, 2023 Prawdopodobieństwo 0 komentarzy

W tym artykule wyjaśniono, czym jest rozkład chi-kwadrat i do czego się go stosuje. Dodatkowo znajdziesz wykres rozkładu chi-kwadrat i jego właściwości.

Jaki jest rozkład chi-kwadrat?

Rozkład chi-kwadrat jest rozkładem prawdopodobieństwa, którego symbolem jest χ². Dokładniej, rozkład chi-kwadrat jest sumą kwadratów k niezależnych zmiennych losowych o rozkładzie normalnym.

Zatem rozkład Chi-kwadrat ma k stopni swobody. Dlatego rozkład Chi-kwadrat ma tyle stopni swobody, ile reprezentuje suma kwadratów zmiennych o rozkładzie normalnym.

$\displaystyle X\sim\chi^2_k \ \color{orange}\bm{\longrightarrow}\color{black}\ \begin{array}{l}\text{Distribuci\'on chi-cuadrado}\\[2ex]\text{con k grados de libertad}\end{array}$

Rozkład Chi-kwadrat jest również znany jako rozkład Pearsona .

Należy zauważyć, że rozkład Chi-kwadrat jest szczególnym przypadkiem rozkładu gamma.

Rozkład chi-kwadrat jest szeroko stosowany we wnioskowaniu statystycznym, na przykład w testowaniu hipotez i przedziałach ufności. Zobaczymy poniżej, jakie są zastosowania tego typu rozkładu prawdopodobieństwa.

Wykres rozkładu chi-kwadrat

Kiedy już zobaczymy definicję rozkładu chi-kwadrat, zobaczymy kilka przykładów tego typu rozkładu przedstawionych graficznie. Poniżej możesz zobaczyć, jak wykres prawdopodobieństwa rozkładu chi-kwadrat zmienia się w zależności od stopni swobody.

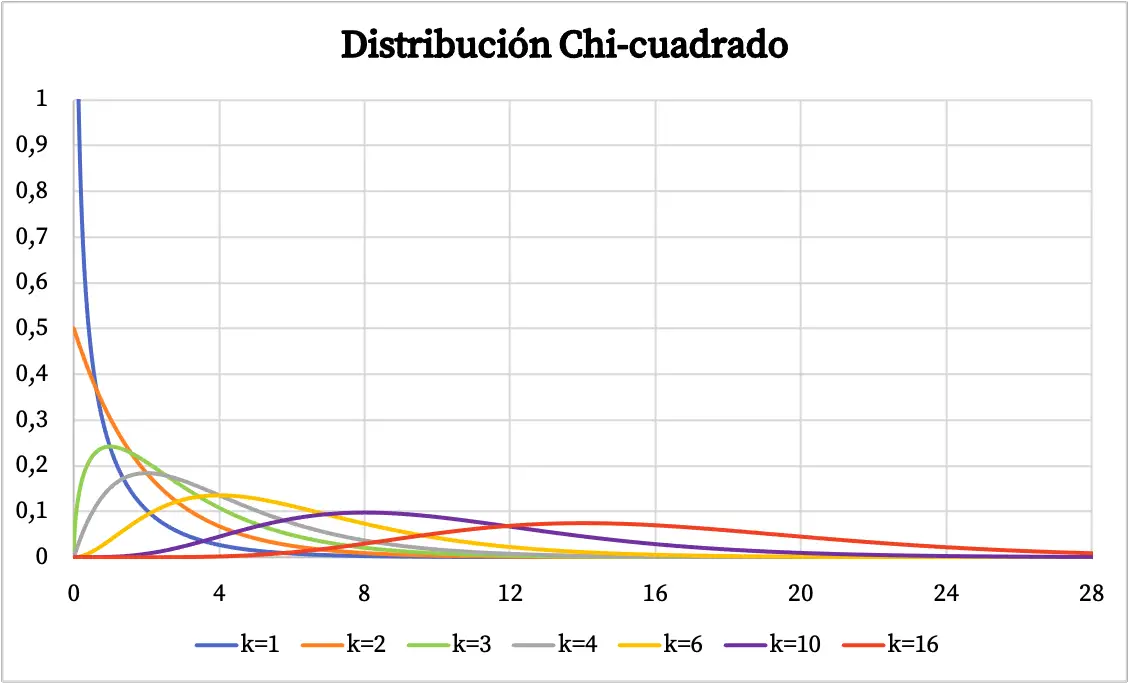
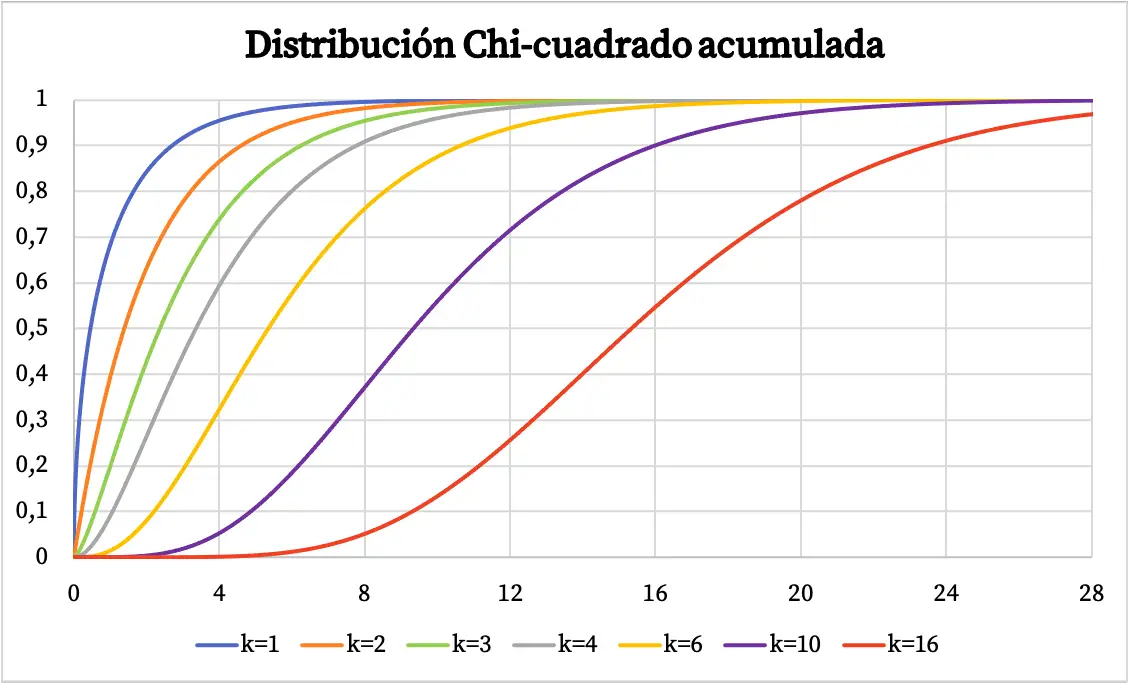
Funkcję gęstości rozkładu chi-kwadrat przedstawiono na powyższym wykresie. Natomiast wykres funkcji skumulowanego rozkładu prawdopodobieństwa chi-kwadrat wygląda następująco:

wykres skumulowanego rozkładu chi-kwadrat

➤ Zobacz: Tabela rozkładu chi-kwadrat

Charakterystyka rozkładu chi-kwadrat

W tej sekcji zobaczymy najważniejsze właściwości rozkładu Chi-kwadrat związane z teorią prawdopodobieństwa i statystyką.

Średnia rozkładu chi-kwadrat jest równa jego stopniom swobody.

$\begin{array}{c}X\sim\chi^2_k\\[2ex] E[X]=k\end{array}$

Wariancja rozkładu chi-kwadrat jest równa dwukrotności stopni swobody rozkładu.

$\begin{array}{c}X\sim\chi^2_k\\[2ex] Var(X)=2\cdot k\end{array}$

Tryb rozkładu chi-kwadrat jest o dwie jednostki mniejszy niż jego stopnie swobody, o ile rozkład ma więcej niż jeden stopień swobody.

$Mo=k-2 \qquad \text{si } k\geq 2$

Funkcja gęstości rozkładu chi-kwadrat wynosi zero, jeśli x=0. Jednakże dla wartości x większych niż 0 funkcję gęstości rozkładu Chi-kwadrat definiuje następujący wzór:

$\displaystyle P[X=x]= \frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}$

Dystrybuantę dystrybucyjną chi-kwadrat reguluje następujący wzór:

$\displaystyle P[X\leq x]=\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}$

Współczynnik skośności rozkładu chi-kwadrat jest pierwiastkiem kwadratowym z ilorazu ośmiu podzielonego przez liczbę stopni swobody rozkładu.

$\displaystyle A=\sqrt{\frac{8}{k}}$

Kurtozę rozkładu Chi-kwadrat oblicza się za pomocą następującego wyrażenia:

$C=3+\cfrac{12}{k}$

Dzięki centralnemu twierdzeniu granicznemu rozkład chi-kwadrat można aproksymować rozkładem normalnym, jeśli k jest wystarczająco duże.

$\displaystyle\lim_{k \to \infty} \frac{\chi^2_k (x)}{ k } = N_{\left(1,\sqrt{2/k}\right)} (x)$

Zastosowania rozkładu chi-kwadrat

Rozkład chi-kwadrat ma wiele różnych zastosowań w statystyce. W rzeczywistości istnieje nawet test chi-kwadrat, który służy do sprawdzania niezależności między zmiennymi i dopasowania do rozkładu teoretycznego. Na przykład test Chi-kwadrat można zastosować do ustalenia, czy dane próbki są zgodne z rozkładem Poissona.

W analizie regresji liniowej rozkład chi-kwadrat jest również używany do szacowania średniej populacji o rozkładzie normalnym i do szacowania nachylenia linii badania regresji liniowej.

Wreszcie rozkład Chi-kwadrat również uczestniczy w analizie wariancji poprzez swój związek z rozkładem Snedecor F.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej