Rozkład częstotliwości

W tym artykule wyjaśniono, czym są rozkłady częstotliwości i jak je osiągnąć. Znajdziesz tu również przykłady rozkładów częstotliwości krok po kroku, a dodatkowo będziesz mógł poćwiczyć z rozwiązanymi ćwiczeniami.

Co to jest rozkład częstotliwości?

W statystyce rozkład częstotliwości to tabela, w której różne wartości próbki są pogrupowane w wiersze, a w każdej kolumnie wyświetlany jest typ częstotliwości każdej wartości. Dlatego rozkład częstotliwości służy do pokazania wszystkich typów częstotliwości w zbiorze danych.

Dokładniej, rozkład częstotliwości obejmuje częstotliwość bezwzględną, skumulowaną częstotliwość bezwzględną, częstotliwość względną i skumulowaną częstotliwość względną.

Jedną z cech rozkładów częstotliwości jest to, że są one bardzo przydatne do podsumowywania próby statystycznej zmiennej ilościowej i zmiennej jakościowej.

Jak dokonać rozkładu częstotliwości

Aby przeprowadzić rozkład częstotliwości, należy wykonać następujące kroki:

1. Uporządkuj dane w różne kategorie i utwórz tabelę, w której każdy wiersz odpowiada kategorii.
2. Oblicz bezwzględną częstotliwość każdej kategorii w drugiej kolumnie tabeli.
3. Oblicz skumulowaną bezwzględną częstotliwość każdej kategorii w trzeciej kolumnie tabeli.
4. Oblicz względną częstotliwość każdej kategorii w czwartej kolumnie tabeli.
5. Oblicz skumulowaną względną częstotliwość każdej kategorii w piątej kolumnie tabeli.
6. Opcjonalnie można dodać dwie kolumny, w których częstotliwość względna i skumulowana częstotliwość względna są obliczane procentowo, w tym celu wystarczy pomnożyć obie kolumny przez 100.

Przykład rozkładu częstotliwości

Kiedy już zapoznaliśmy się z definicją rozkładu częstotliwości i teorią jego konstrukcji, w tej sekcji przykład zostanie rozwiązany krok po kroku.

• Oceny uzyskane z przedmiotu statystyka w klasie 30 uczniów przedstawiają się następująco. Skonstruuj rozkład częstotliwości zbioru danych.

Ponieważ wszystkie liczby mogą być tylko liczbami całkowitymi, jest to zmienna dyskretna. Nie jest zatem konieczne grupowanie danych w przedziały.

Aby więc sporządzić rozkład częstotliwości, musimy skonstruować tabelę, w której każda inna wartość będzie wierszem, a następnie musimy znaleźć częstotliwość bezwzględną każdej wartości:

Należy pamiętać, że suma wszystkich częstotliwości bezwzględnych jest równa całkowitej liczbie danych. Jeśli zasada ta nie będzie przestrzegana, oznacza to, że zapomniałeś podać pewnych informacji.

Teraz, gdy znamy częstotliwość bezwzględną, musimy obliczyć skumulowaną częstotliwość bezwzględną. Do tego obliczenia mamy dwie możliwości: albo dodajemy częstotliwość bezwzględną wartości plus wszystkie częstotliwości bezwzględne najmniejszych wartości, albo odwrotnie, dodajemy częstotliwość bezwzględną wartości plus skumulowaną częstotliwość bezwzględną poprzedniej wartości.

Skumulowana częstotliwość bezwzględna ostatniej wartości zawsze odpowiada całkowitej liczbie danych. Możesz skorzystać z tej sztuczki, aby sprawdzić, czy obliczenia są prawidłowe.

Następnie musimy określić częstotliwość względną, którą obliczamy poprzez podzielenie częstotliwości bezwzględnej przez całkowitą liczbę punktów danych (30):

Należy pamiętać, że suma wszystkich częstotliwości względnych zawsze wynosi 1, w przeciwnym razie oznacza to, że pewne obliczenia rozkładu częstotliwości są błędne.

Na koniec musimy po prostu wyodrębnić skumulowaną częstotliwość względną. Aby to zrobić, należy dodać częstotliwość względną danej wartości plus wszystkie poprzednie częstotliwości względne lub, co sprowadza się do tego samego, poprzednią skumulowaną częstotliwość względną:

Krótko mówiąc, rozkład częstotliwości ze wszystkimi częstotliwościami danych problemowych jest następujący:

Rozkład częstotliwości dla danych pogrupowanych

Aby utworzyć rozkład częstotliwości dla danych pogrupowanych w przedziały , jedyną różnicą jest to, że zbiór danych należy najpierw pogrupować w różne przedziały, a pozostałe obliczenia wykonuje się w taki sam sposób, jak w przypadku rozkładu częstotliwości bez grupowania danych.

Jako przykład, poniżej rozwiązano problem konstruowania rozkładu częstotliwości dla zgrupowanych danych.

• Zmierzono wzrost 20 osób i uzyskano wyniki podane poniżej. Utwórz rozkład częstotliwości, dzieląc dane na przedziały.

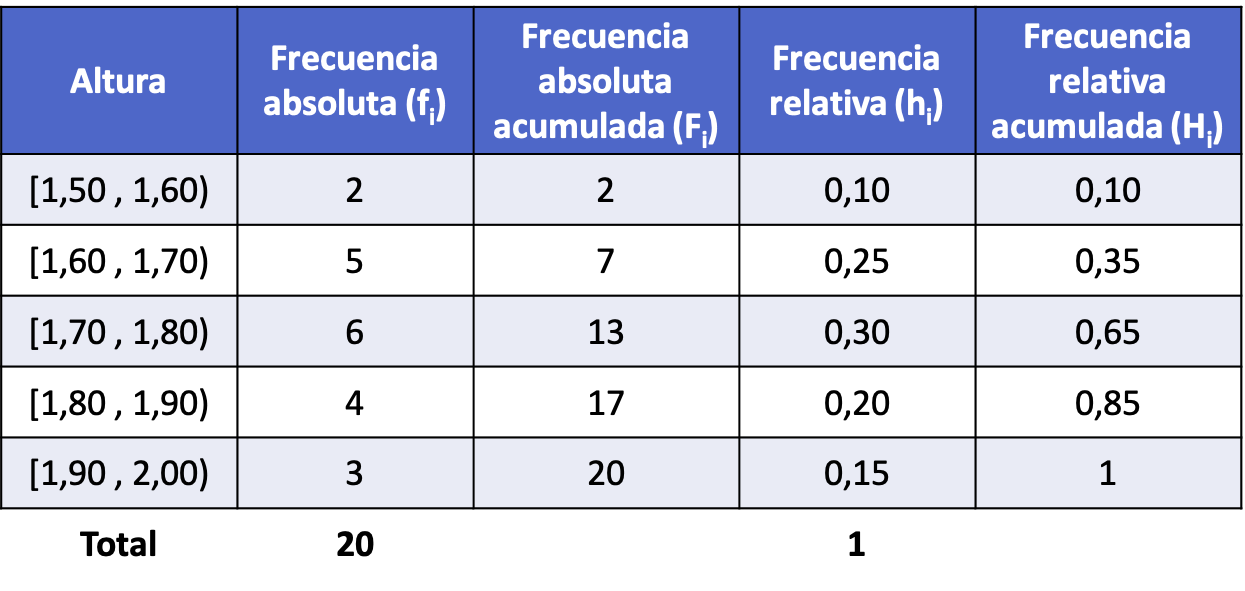
Dane w tej próbce mają rozkład ciągły, ponieważ liczby mogą być ułamkami dziesiętnymi i dlatego mogą przyjmować dowolną wartość. Dlatego zrobimy rozkład częstotliwości grupujący dane w przedziały.

Chociaż istnieje kilka matematycznych zasad tworzenia odstępów próbki, w tym przypadku po prostu utworzymy odstępy o szerokości 10 dziesiątych.

Zatem po obliczeniu wszystkich typów częstotliwości dla każdego przedziału (procedura jest taka sama jak w powyższym przykładzie) rozkład częstotliwości przy danych pogrupowanych w przedziały wygląda następująco:

Rozwiązane ćwiczenia dotyczące rozkładu częstotliwości

Ćwiczenie 1

Zapytaliśmy 20 osób, ile razy w miesiącu chodzą do kina i oto wyniki:

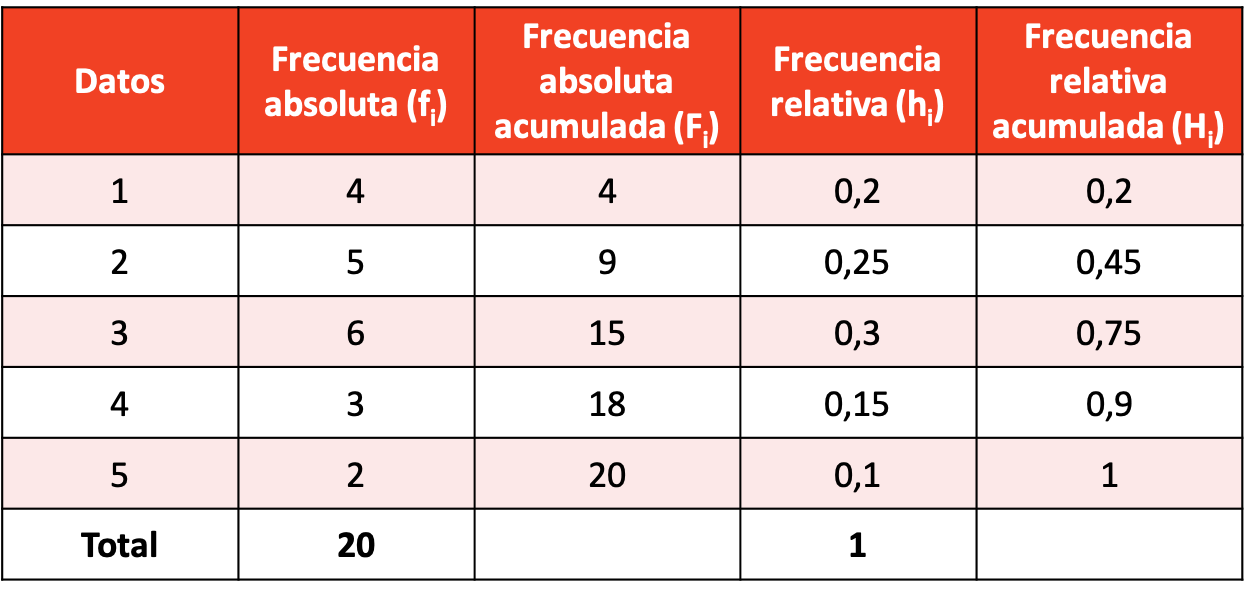
Dokonaj rozkładu częstotliwości na podstawie otrzymanej próbki danych.

Rozkład częstotliwości z obliczeniami wszystkich typów częstotliwości wygląda następująco:

Ćwiczenie 2

Chciałbyś przeprowadzić badanie statystyczne dotyczące masy pracowników w firmie zatrudniającej 36 pracowników. Oto masa robotników wyrażona w kilogramach:

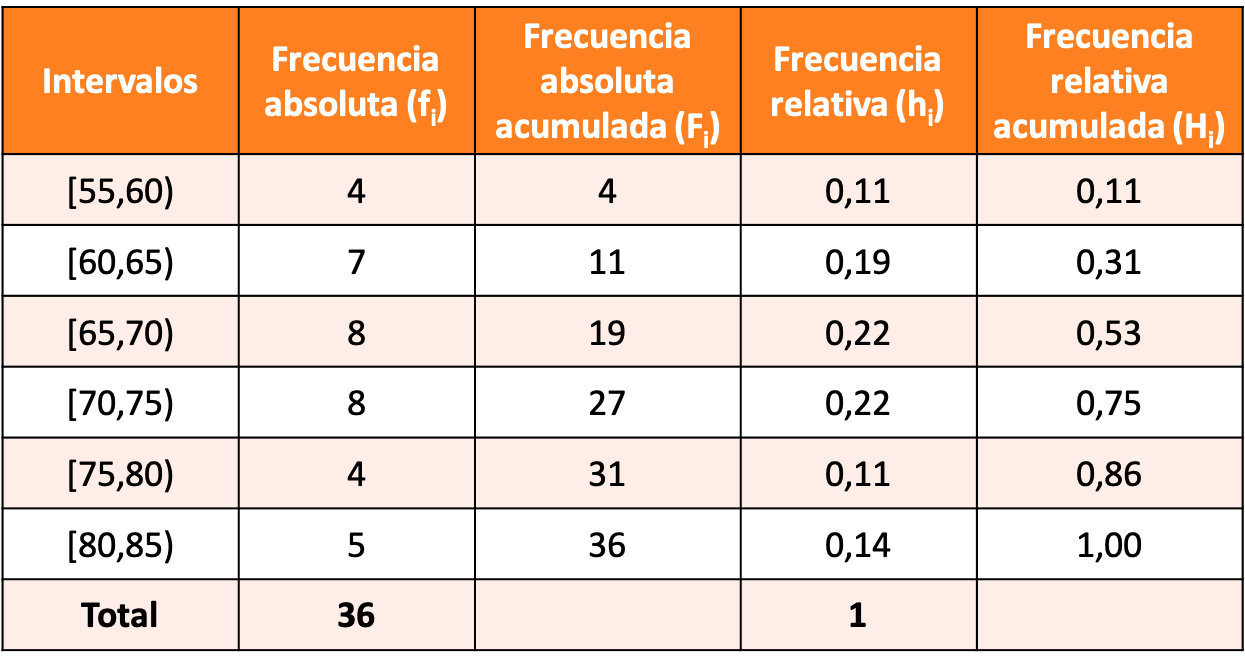
Skonstruuj rozkład częstotliwości z pogrupowanymi danymi, tworząc przedziały o długości 5 jednostek i niech pierwszy przedział będzie wynosić [55,60).

Rozwiązaniem ćwiczenia jest następujący rozkład częstotliwości: