Wprowadzenie do rozkładu dwumianowego

Rozkład dwumianowy jest jednym z najpopularniejszych rozkładów w statystyce. Aby zrozumieć rozkład dwumianowy, warto najpierw zrozumieć eksperymenty dwumianowe .

Eksperymenty dwumianowe

Eksperyment dwumianowy to eksperyment, który ma następujące właściwości:

• Doświadczenie składa się z n powtarzanych prób.
• Każda próba ma tylko dwa możliwe wyniki.
• Prawdopodobieństwo sukcesu, oznaczone p , jest takie samo dla każdej próby.
• Każdy test jest niezależny.

Najbardziej oczywistym przykładem eksperymentu dwumianowego jest rzut monetą. Załóżmy na przykład, że rzucamy monetą 10 razy. Jest to eksperyment dwumianowy, ponieważ ma następujące cztery właściwości:

• Eksperyment składa się z n powtarzanych prób – Jest 10 prób.
• Każda próba ma tylko dwa możliwe wyniki: orzeł lub reszka.
• Prawdopodobieństwo sukcesu, oznaczone p , jest takie samo dla każdej próby. Jeśli zdefiniujemy „sukces” jako główkę do lądowania, wówczas prawdopodobieństwo sukcesu wynosi dokładnie 0,5 dla każdej próby.
• Każda próba jest niezależna – wynik jednego rzutu monetą nie ma wpływu na wynik żadnego innego rzutu monetą.

Rozkład dwumianowy

Rozkład dwumianowy opisuje prawdopodobieństwo uzyskania k sukcesów w n eksperymentach dwumianowych.

Jeśli zmienna losowa X ma rozkład dwumianowy, prawdopodobieństwo, że X = k powodzenia można obliczyć za pomocą następującego wzoru:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Złoto:

• n: liczba prób
• k: liczba sukcesów
• p: prawdopodobieństwo sukcesu w danej próbie
• _n C _k : liczba sposobów uzyskania k sukcesów w n próbach

Załóżmy na przykład, że rzucamy monetą 3 razy. Możemy użyć powyższego wzoru, aby określić prawdopodobieństwo uzyskania 0, 1, 2 i 3 orłów w tych 3 rzutach:

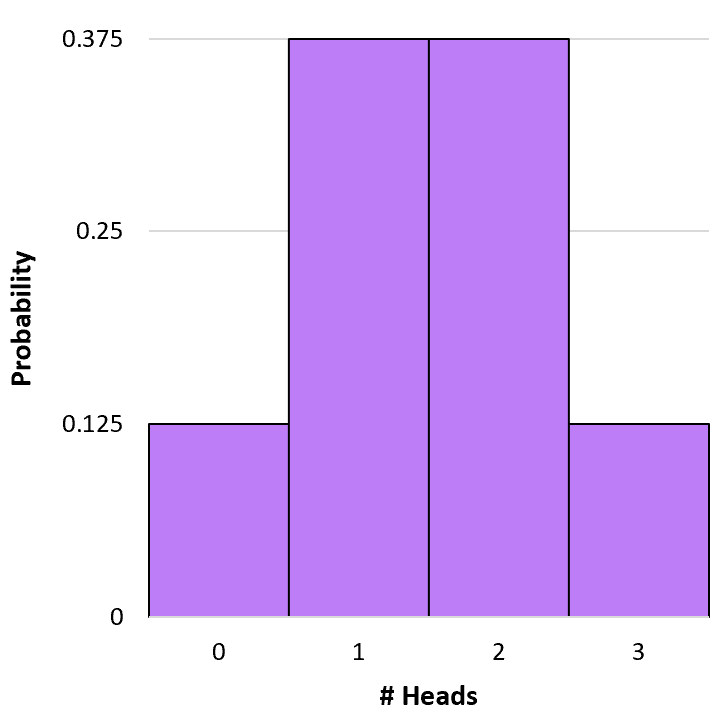
P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125

P(X=1) = ₃ C ₁ * 0,5 ¹ * (1-0,5) ^3-1 = 3 * 0,5 * (0,5) ² = 0,375

P(X=2) = ₃ C ₂ * 0,5 ² * (1-0,5) ^3-2 = 3 * 0,25 * (0,5) ¹ = 0,375

P(X=3) = ₃ C ₃ * 0,5 ³ * (1-0,5) ^3-3 = 1 * 0,125 * (0,5) ⁰ = 0,125

Uwaga : Użyliśmy tego połączonego kalkulatora do obliczenia _{nCk dla} każdego przykładu.

Możemy utworzyć prosty histogram, aby zwizualizować ten rozkład prawdopodobieństwa:

Obliczanie skumulowanych prawdopodobieństw dwumianowych

Za pomocą powyższego wzoru można łatwo obliczyć pojedyncze prawdopodobieństwo dwumianowe (np. prawdopodobieństwo, że moneta wypadnie reszką 1 raz w 3 rzutach), ale aby obliczyć skumulowane prawdopodobieństwa dwumianowe, musimy dodać prawdopodobieństwa indywidualne.

Załóżmy na przykład, że chcemy poznać prawdopodobieństwo, że moneta wypadnie orzeł 1 lub mniej razy w 3 rzutach. Do obliczenia tego prawdopodobieństwa użyjemy następującego wzoru:

P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .

Nazywa się to prawdopodobieństwem skumulowanym , ponieważ polega na dodaniu wielu prawdopodobieństw. Możemy obliczyć skumulowane prawdopodobieństwo uzyskania k lub mniej orłów dla każdego wyniku, korzystając z podobnego wzoru:

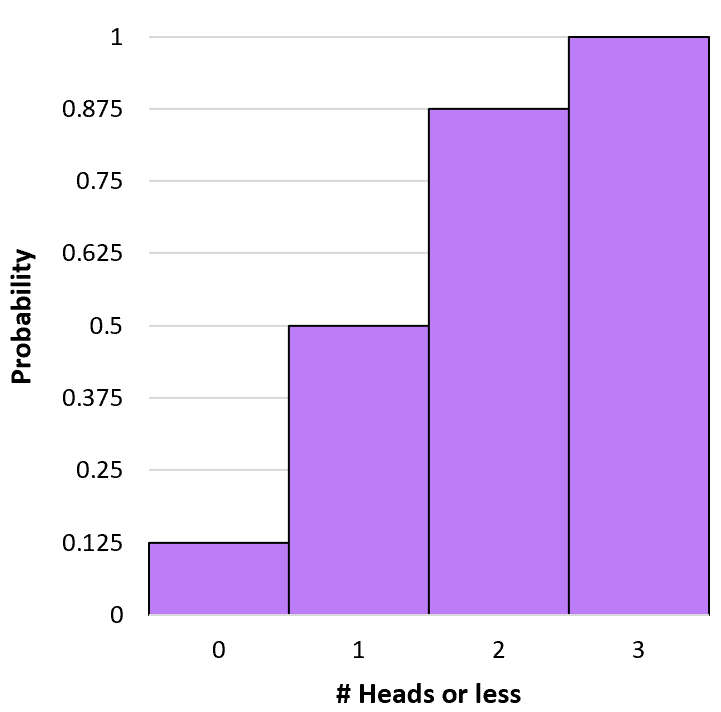
P(X≤0) = P(X=0) = 0,125 .

P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .

P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0,125 + 0,375 + 0,375 = 0,875 .

P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0,125 + 0,375 + 0,375 + 0,125 = 1 .

Możemy utworzyć histogram, aby zwizualizować ten skumulowany rozkład prawdopodobieństwa:

Kalkulator prawdopodobieństwa dwumianowego

Kiedy pracujemy z małymi liczbami (np. 3 rzuty monetą), rozsądne jest ręczne obliczenie prawdopodobieństw dwumianowych. Jeśli jednak pracujemy z większymi liczbami (np. 100 losowań), ręczne obliczenie prawdopodobieństwa może być trudne. W takich przypadkach pomocne może być skorzystanie z kalkulatora prawdopodobieństwa dwumianowego, takiego jak ten poniżej.

Załóżmy na przykład, że rzucamy monetą n = 100 razy, prawdopodobieństwo, że wypadnie reszka w danej próbie wynosi p = 0,5, a chcemy poznać prawdopodobieństwo wyrzucenia reszki k = 43 razy lub mniej:

Oto jak zinterpretować wynik:

• Prawdopodobieństwo, że na monecie wypadnie orzeł dokładnie 43 razy, wynosi 0,03007 .
• Prawdopodobieństwo, że na monecie wypadnie orzeł mniej niż 43 razy, wynosi 0,06661 .
• Prawdopodobieństwo, że na monecie wypadnie orzeł 43 lub mniej, wynosi 0,09667 .
• Prawdopodobieństwo, że na monecie wypadnie orzeł więcej niż 43 razy, wynosi 0,90333 .
• Prawdopodobieństwo, że na monecie wypadnie orzeł 43 lub więcej razy, wynosi 0,93339 .

Własności rozkładu dwumianowego

Rozkład dwumianowy ma następujące właściwości:

Średnia rozkładu wynosi μ = np

Wariancja rozkładu wynosi σ ² = np(1-p)

Odchylenie standardowe rozkładu wynosi σ = √ np(1-p)

Załóżmy na przykład, że rzucamy monetą 3 razy. Niech p = prawdopodobieństwo, że moneta wyląduje na orle.

Średnia liczba głów, której się spodziewamy, wynosi μ = np = 3*.5 = 1,5 .

Oczekiwana wariancja liczby głów wynosi σ ² = np(1-p) = 3*.5*(1-.5) = 0.75 .

Problemy z praktyką rozkładu dwumianowego

Skorzystaj z poniższych problemów praktycznych, aby sprawdzić swoją wiedzę na temat rozkładu dwumianowego.

Problem 1

Pytanie: Bob wykonuje 60% swoich prób rzutów wolnych. Jeśli wykona 12 rzutów wolnych, jakie jest prawdopodobieństwo, że trafi dokładnie 10?

Odpowiedź: Używając powyższego kalkulatora rozkładu dwumianowego dla p = 0,6, n = 12 i k = 10, stwierdzamy, że P(X=10) = 0,06385 .

Problem 2

Pytanie: Jessica rzuca monetą 5 razy. Jakie jest prawdopodobieństwo, że na monecie wypadnie reszka 2 lub mniej?

Odpowiedź: Używając powyższego kalkulatora rozkładu dwumianowego dla p = 0,5, n = 5 i k = 2, stwierdzamy, że P(X≤2) = 0,5 .

Problem 3

Pytanie: Prawdopodobieństwo, że dany student zostanie przyjęty na określoną uczelnię wynosi 0,2. Jeżeli aplikuje 10 studentów, jakie jest prawdopodobieństwo, że zostanie przyjętych więcej niż 4?

Odpowiedź: Używając powyższego kalkulatora rozkładu dwumianowego dla p = 0,2, n = 10 i k = 4, stwierdzamy, że P(X>4) = 0,03279 .

Problem 4

Pytanie: Rzucasz monetą 12 razy. Jaka jest oczekiwana średnia liczba głów, które się pojawią?

Odpowiedź: Przypomnijmy, że średnią rozkładu dwumianowego oblicza się jako μ = np. Zatem μ = 12*0,5 = 6 głów .

Problem 5

Pytanie: Marek trafia home run w 10% swoich prób. Jeśli w danej grze uda mu się uzyskać 5 prób, jaka jest różnica w liczbie home runów, które uda mu się wykonać?

Odpowiedź: Przypomnijmy, że wariancję rozkładu dwumianowego oblicza się jako σ ² = np(1-p). Zatem ^σ2 = 6*,1*(1-,1) = 0,54 .

Dodatkowe zasoby

Poniższe artykuły mogą pomóc Ci nauczyć się korzystać z rozkładu dwumianowego w różnych programach statystycznych:

• Jak obliczyć prawdopodobieństwa dwumianowe w programie Excel
• Jak obliczyć prawdopodobieństwa dwumianowe na kalkulatorze TI-84
• Jak obliczyć prawdopodobieństwa dwumianowe w R
• Jak wykreślić rozkład dwumianowy w R