Wprowadzenie do rozkładu geometrycznego

Rozkład geometryczny opisuje prawdopodobieństwo wystąpienia określonej liczby niepowodzeń przed osiągnięciem pierwszego sukcesu w serii prób Bernoulliego.

Próba Bernoulliego to eksperyment, w którym możliwe są tylko dwa wyniki – „sukces” lub „porażka”, a prawdopodobieństwo sukcesu jest takie samo za każdym razem, gdy eksperyment jest przeprowadzany.

Przykładem eseju Bernoulliego jest rzut monetą. Moneta może wylądować tylko na dwóch orłach (możemy nazwać orzeł „trafieniem”, a reszkę „porażką”), a prawdopodobieństwo powodzenia w każdym rzucie wynosi 0,5, zakładając, że moneta jest uczciwa.

Jeśli zmienna losowa X ma rozkład geometryczny, wówczas prawdopodobieństwo wystąpienia k niepowodzeń przed pierwszym sukcesem można obliczyć za pomocą następującego wzoru:

P(X=k) = (1-p) ^kp

Złoto:

• k: liczba niepowodzeń przed pierwszym sukcesem
• p: prawdopodobieństwo sukcesu w każdej próbie

Załóżmy na przykład, że chcemy wiedzieć, ile razy musimy rzucić uczciwą monetą, aż wypadnie reszka. Możemy skorzystać z powyższego wzoru, aby określić prawdopodobieństwo wystąpienia 0, 1, 2, 3 awarii itp. zanim moneta wyląduje na reszcie:

Uwaga: moneta może doznać 0 „porażek”, jeśli w pierwszym rzucie wypadnie reszka.

P(X=0) = (1-0,5) ⁰ (0,5) = 0,5

P(X=1) = (1-0,5) ¹ (0,5) = 0,25

P(X=2) = (1-0,5) ² (0,5) = 0,125

P(X=3) = (1-0,5) ³ (0,5) = 0,0625

Prawdopodobieństwo dowolnej liczby rzutów monetą możemy obliczyć aż do nieskończoności. Następnie tworzymy prosty histogram, aby zwizualizować ten rozkład prawdopodobieństwa:

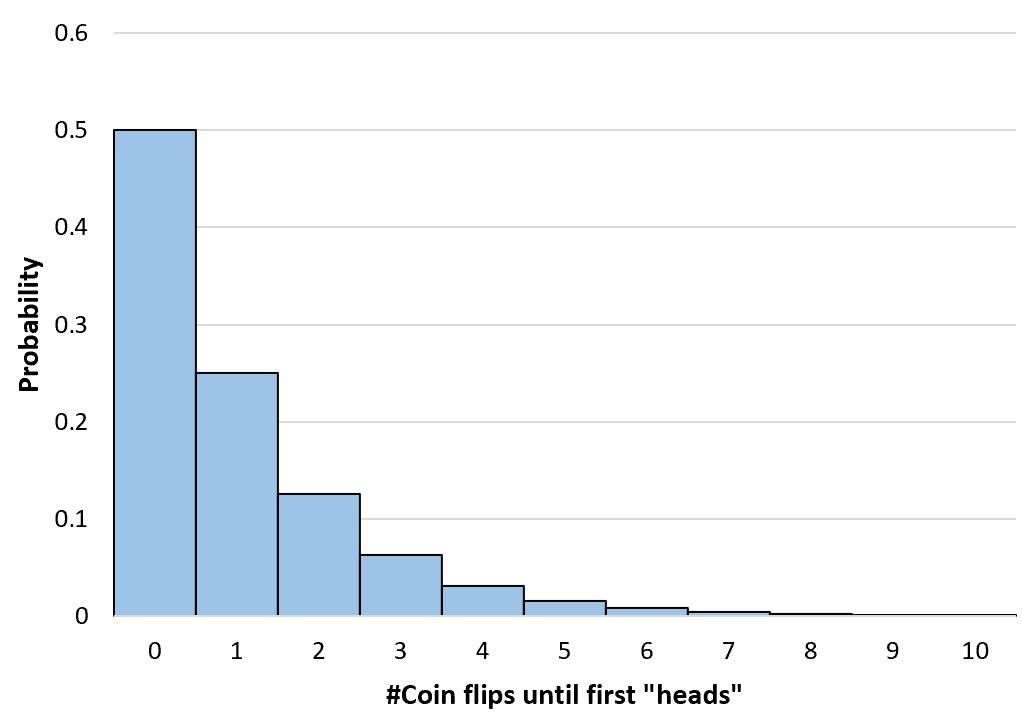
Obliczanie skumulowanych prawdopodobieństw geometrycznych

Skumulowane prawdopodobieństwo , że do pierwszego sukcesu doświadczymy k lub mniej niepowodzeń, można obliczyć za pomocą następującego wzoru:

P(X≤k) = 1 – (1-p) ^k+1

Złoto:

• k: liczba niepowodzeń przed pierwszym sukcesem
• p: prawdopodobieństwo sukcesu w każdej próbie

Załóżmy na przykład, że chcemy poznać prawdopodobieństwo, że upłyną trzy lub mniej „chybienia”, zanim moneta ostatecznie wyląduje na orle. Do obliczenia tego prawdopodobieństwa użyjemy następującego wzoru:

P(X≤3) = 1 – (1-0,5) ³⁺¹ = 0,9375

Każde skumulowane prawdopodobieństwo możemy obliczyć za pomocą podobnego wzoru:

P(X≤0) = 1 – (1-.5) ⁰⁺¹ = 0,5

P(X≤1) = 1 – (1-0,5) ¹⁺¹ = 0,75

P(X≤2) = 1 – (1-0,5) ²⁺¹ = 0,875

Możemy obliczyć te skumulowane prawdopodobieństwa dla dowolnej liczby rzutów monetą aż do nieskończoności. Następnie możemy utworzyć histogram, aby zwizualizować ten skumulowany rozkład prawdopodobieństwa:

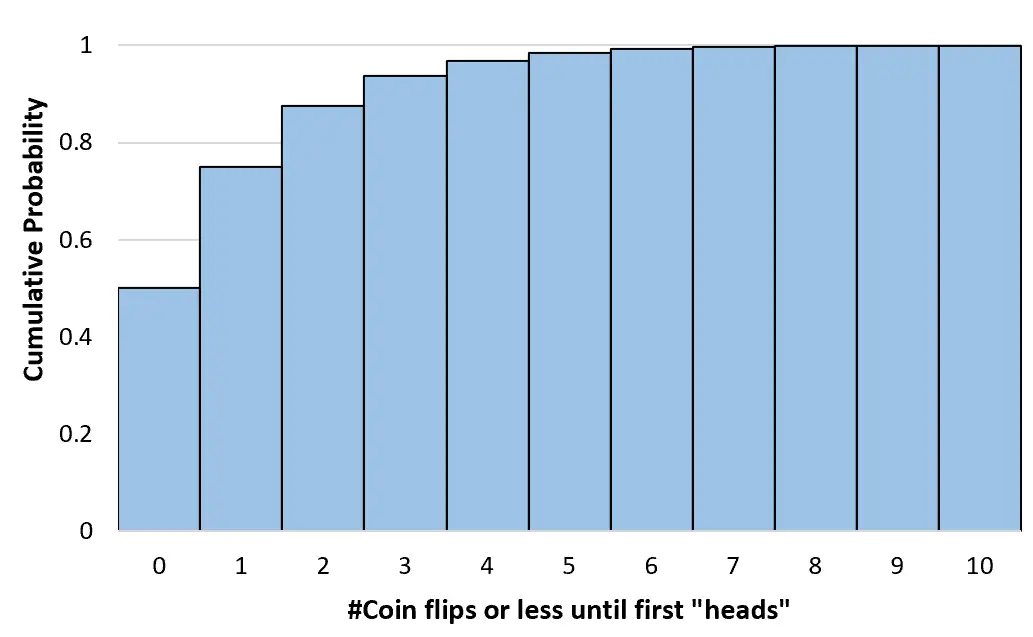
Własności rozkładu geometrycznego

Rozkład geometryczny ma następujące właściwości:

Średnia rozkładu wynosi (1-p) / p .

Wariancja rozkładu wynosi (1-p) / p ² .

Na przykład:

Średnia liczba przypadków, w których spodziewamy się, że moneta wyrzuci reszkę, zanim wyląduje reszka, będzie wynosić (1-p) / p = (1-0,5) / 0,5 = 1 .

Wariancja liczby rzutów, aż do wylądowania na orle, będzie wynosić (1-p)/ ^p2 =(1-0,5)/. ⁵² = 2 .

Problemy praktyki rozkładu geometrycznego

Skorzystaj z poniższych zadań praktycznych, aby sprawdzić swoją wiedzę na temat rozkładu geometrycznego.

Uwaga: Do obliczenia odpowiedzi na te pytania użyjemy kalkulatora rozkładu geometrycznego .

Problem 1

Pytanie: Badacz czeka przed biblioteką, aby zapytać ludzi, czy popierają określone prawo. Prawdopodobieństwo, że dana osoba popiera prawo, wynosi p = 0,2. Jakie jest prawdopodobieństwo, że czwarta osoba, z którą rozmawia badacz, jako pierwsza poprze prawo?

Odpowiedź: Liczba „porażek” do pierwszego sukcesu – czyli liczba osób, które nie poprzeją prawa, dopóki nie poprze go pierwsza osoba – wynosi 3. Zatem korzystając z kalkulatora rozkładu geometrycznego przy p = 0,2 i x = 3 niepowodzenia, stwierdzamy, że P(X=3) = 0,10240 .

Problem 2

Pytanie: Badacz czeka przed biblioteką, aby zapytać ludzi, czy popierają określone prawo. Prawdopodobieństwo, że dana osoba popiera prawo, wynosi p = 0,2. Jakie jest prawdopodobieństwo, że badacz musiałby porozmawiać z więcej niż czterema osobami, aby znaleźć kogoś, kto popiera prawo?

Odpowiedź: Korzystając z kalkulatora rozkładu geometrycznego przy błędach p = 0,2 i x = 4, stwierdzamy, że P(X>4) = 0,32768 .

Problem 3

Pytanie: Badacz czeka przed biblioteką, aby zapytać ludzi, czy popierają określone prawo. Prawdopodobieństwo, że dana osoba popiera prawo, wynosi p = 0,2. Z jaką przewidywaną liczbą osób badacz będzie musiał porozmawiać, zanim znajdzie kogoś, kto popiera prawo?

Odpowiedź: Przypomnijmy, że średnia rozkładu geometrycznego wynosi (1-p) / p . W tej sytuacji średnia wyniosłaby (1-0,2) / 0,2 = 4 .