Jak korzystać z rozkładu geometrycznego w programie excel

Rozkład geometryczny opisuje prawdopodobieństwo wystąpienia określonej liczby niepowodzeń przed osiągnięciem pierwszego sukcesu w serii prób Bernoulliego.

Próba Bernoulliego to eksperyment, w którym możliwe są tylko dwa wyniki – „sukces” lub „porażka”, a prawdopodobieństwo sukcesu jest takie samo za każdym razem, gdy eksperyment jest przeprowadzany.

Przykładem eseju Bernoulliego jest rzut monetą. Moneta może wylądować tylko na dwóch orłach (możemy nazwać orzeł „trafieniem”, a reszkę „porażką”), a prawdopodobieństwo powodzenia w każdym rzucie wynosi 0,5, zakładając, że moneta jest uczciwa.

Jeśli zmienna losowa X ma rozkład geometryczny, wówczas prawdopodobieństwo wystąpienia k niepowodzeń przed pierwszym sukcesem można obliczyć za pomocą następującego wzoru:

P(X=k) = (1-p) ^kp

Złoto:

• k: liczba niepowodzeń przed pierwszym sukcesem
• p: prawdopodobieństwo sukcesu w każdej próbie

Poniższe przykłady pokazują, jak obliczyć prawdopodobieństwa związane z rozkładem geometrycznym w programie Excel.

Przykład 1: Rzuć monetą

Załóżmy, że rzucamy monetą i chcemy poznać prawdopodobieństwo, że miną dokładnie trzy „chybienia”, zanim w końcu wypadnie reszka.

Do obliczenia tego prawdopodobieństwa użyjemy następującego wzoru:

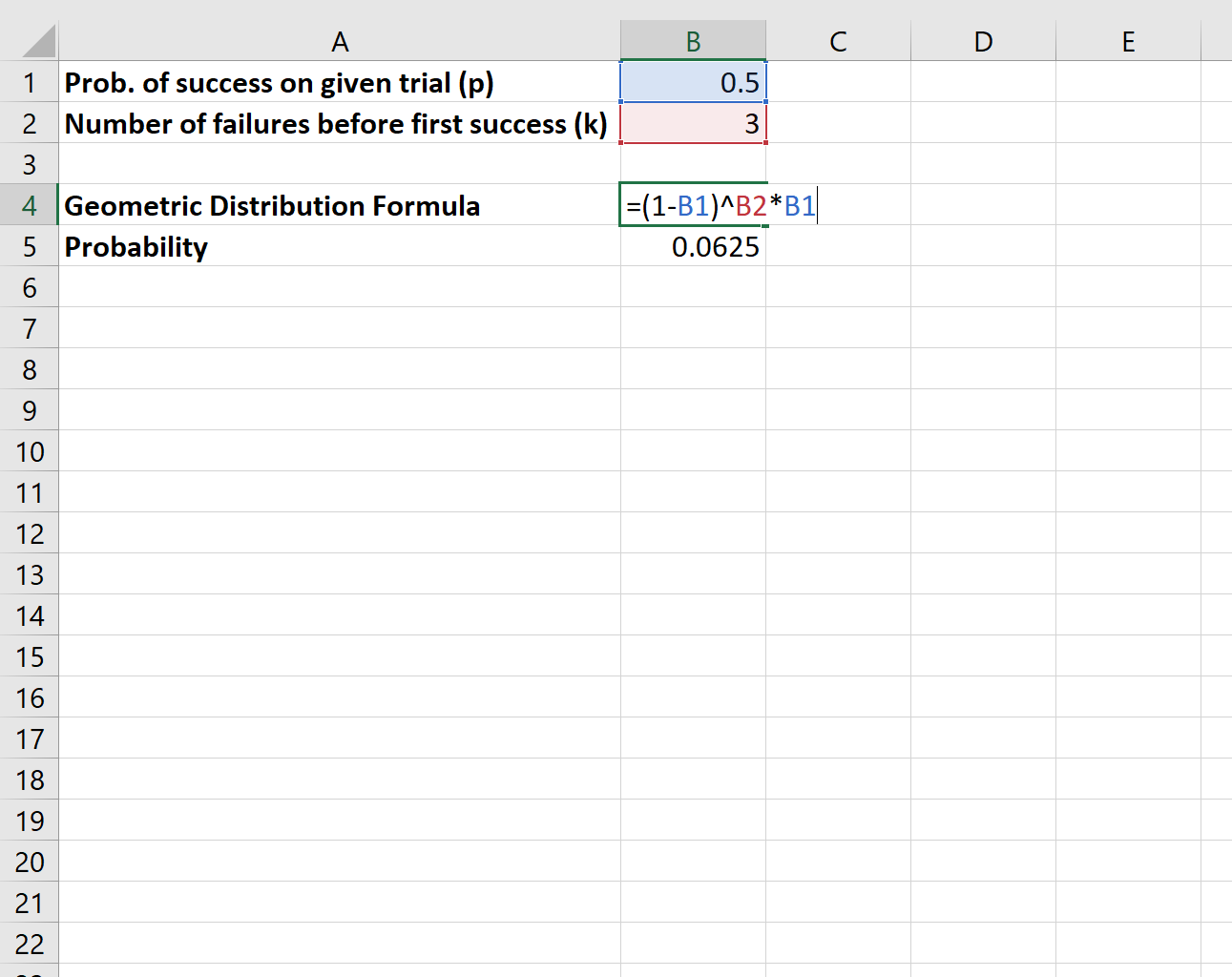
Prawdopodobieństwo, że trzy razy nie trafimy, aż w końcu wypadnie reszka, wynosi 0,0625 .

Przykład 2: Strzelanie z rzutu wolnego

Załóżmy, że pewien koszykarz wykonuje 60% swoich rzutów wolnych. Jakie jest prawdopodobieństwo, że zawodnik nie wykorzysta czterech rzutów wolnych, aż w końcu uda im się wykonać jeden?

Do obliczenia tego prawdopodobieństwa użyjemy następującego wzoru:

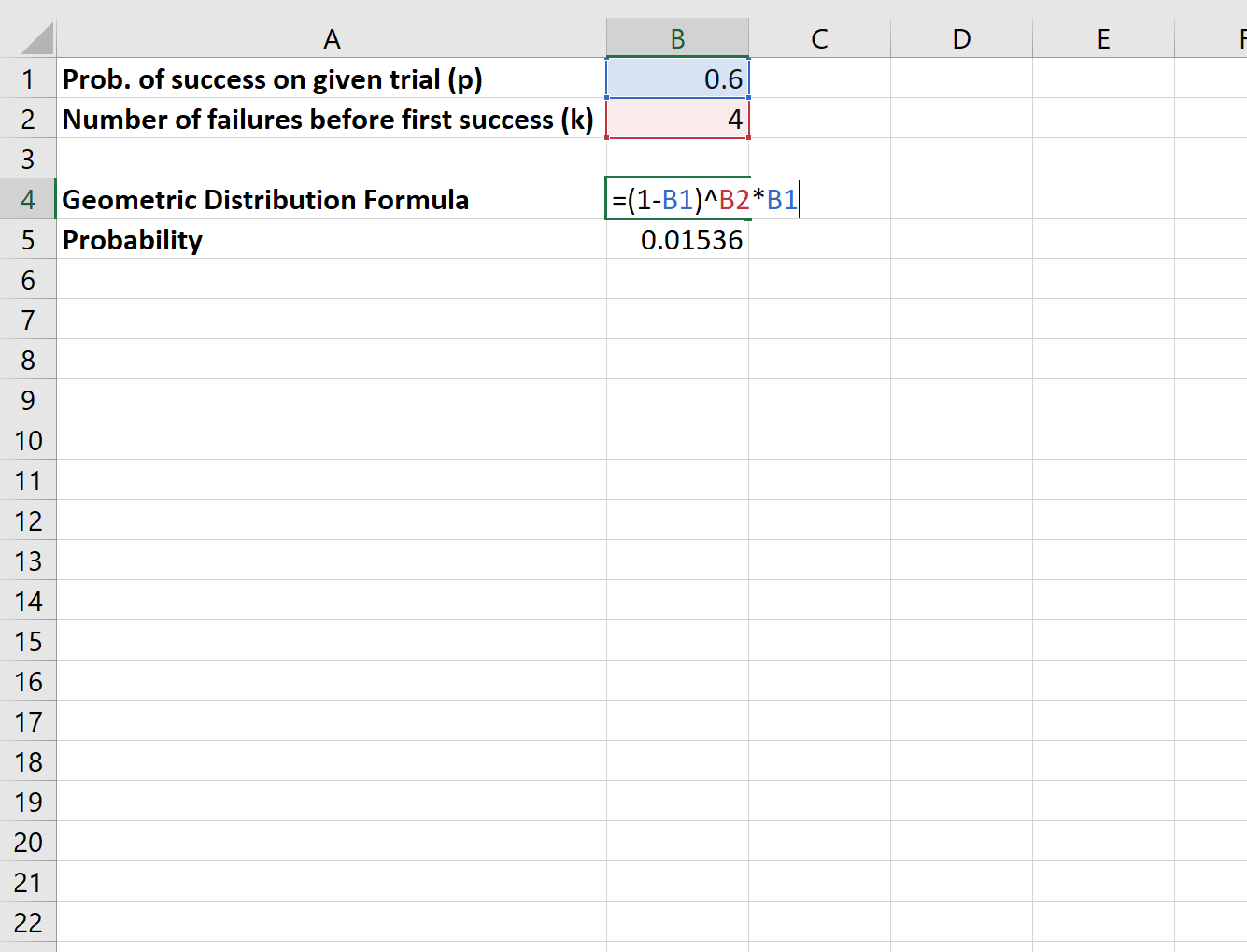
Prawdopodobieństwo, że zawodnik nie wykorzysta czterech rzutów wolnych, aż w końcu wykona jeden, wynosi 0,01536 .

Przykład 3: Wspieranie prawa

Załóżmy, że badacz czeka przed biblioteką, aby zapytać ludzi, czy popierają określone prawo. Prawdopodobieństwo, że dana osoba popiera prawo, wynosi p = 0,2. Jakie jest prawdopodobieństwo, że czwarta osoba, z którą rozmawia badacz, jako pierwsza poprze prawo?

Do obliczenia tego prawdopodobieństwa użyjemy następującego wzoru:

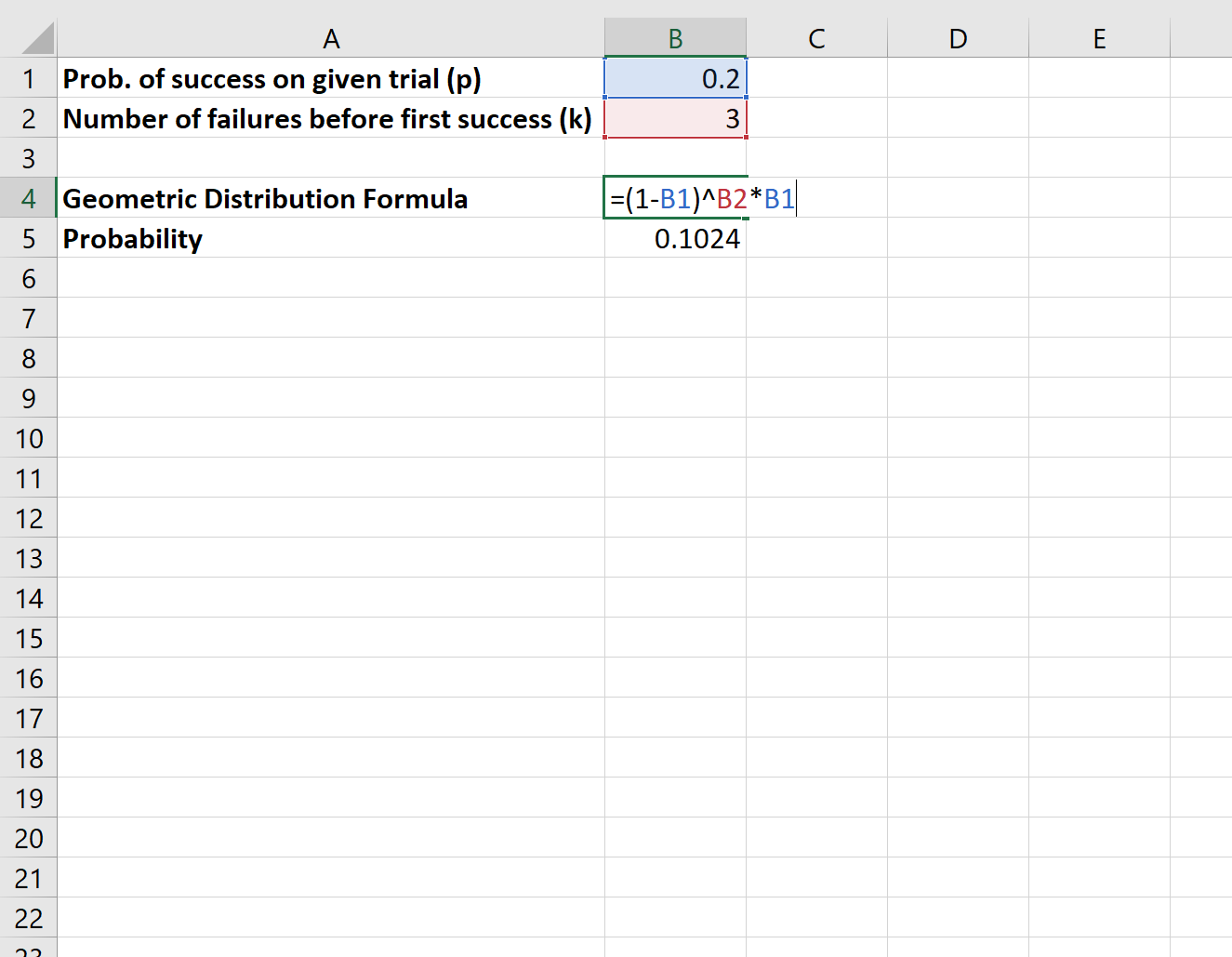
Prawdopodobieństwo, że czwarta osoba, z którą rozmawia badacz, jako pierwsza poprze to prawo, wynosi 0,1024 .

Dodatkowe zasoby

Wprowadzenie do rozkładu geometrycznego
Kalkulator rozkładu geometrycznego
5 konkretnych przykładów rozkładu geometrycznego