Rozkład hipergeometryczny

Przez Benjamin Anderson 6 sierpnia, 2023 Prawdopodobieństwo 0 komentarzy

W tym artykule wyjaśniamy, czym jest rozkład hipergeometryczny i jak oblicza się prawdopodobieństwo dla tego typu rozkładu. W Internecie znajdziesz wzór na rozkład hipergeometryczny, jakie są jego cechy, a także kalkulator pozwalający obliczyć prawdopodobieństwo wystąpienia rozkładu hipergeometrycznego.

Co to jest rozkład hipergeometryczny?

Rozkład hipergeometryczny to rozkład prawdopodobieństwa opisujący liczbę pomyślnych przypadków w losowej ekstrakcji bez zastępowania n elementów z populacji.

Oznacza to, że rozkład hipergeometryczny służy do obliczenia prawdopodobieństwa uzyskania x sukcesów podczas wyodrębniania n elementów z populacji bez zastępowania żadnego z nich.

Rozkład hipergeometryczny ma trzy parametry:

N : to liczba elementów w populacji (N = 0, 1, 2,…).
K : to maksymalna liczba przypadków sukcesu (K = 0, 1, 2,…,N). Ponieważ w rozkładzie hipergeometrycznym element można uznać jedynie za „sukces” lub „porażkę”, NK to maksymalna liczba przypadków awarii.
n : liczba wykonanych pobrań bez zamiany.

$X \sim HG(N,K,n)$

Przykładowo dyskretna zmienna losowa X posiadająca rozkład hipergeometryczny o parametrach N=8, K=5 i n=3 jest zdefiniowana następująco:

$X \sim HG(8,5,3)$

Wzór na rozkład hipergeometryczny

Wzór na rozkład hipergeometryczny jest iloczynem liczby kombinatorycznej K przez x przez liczbę kombinatoryczną NK przez nx podzieloną przez liczbę kombinatoryczną N przez n .

Gdzie N to wielkość populacji, K to całkowita liczba korzystnych przypadków, n to liczba ekstrakcji bez wymiany, a x to liczba korzystnych przypadków, dla których należy obliczyć prawdopodobieństwo wystąpienia.

👉 Za pomocą poniższego kalkulatora możesz obliczyć prawdopodobieństwo zdarzenia zmiennej zgodnej z rozkładem hipergeometrycznym.

Przykład rozkładu hipergeometrycznego

Kiedy już poznaliśmy definicję i wzór rozkładu hipergeometrycznego, teraz rozwiążemy przykład krok po kroku, abyś wiedział, jak obliczyć prawdopodobieństwo rozkładu hipergeometrycznego.

Do worka wkładamy 20 kul niebieskich i 30 czerwonych, czyli w sumie w worku znajduje się 50 kulek. Jeśli wylosujemy 12 kul bez zwracania żadnej, znajdź prawdopodobieństwo wylosowania 4 niebieskich kul.

Pierwszą rzeczą, którą musimy zrobić, aby rozwiązać ćwiczenie, jest identyfikacja parametrów rozkładu hipergeometrycznego. W tym przypadku całkowita liczba elementów w populacji wynosi 50 ( N = 50), maksymalna liczba korzystnych przypadków to 20 ( K = 20) i losowanych jest 12 kul ( n = 12).

$\left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)$

Chcemy obliczyć prawdopodobieństwo wylosowania 4 niebieskich kul ( x =4), dlatego stosujemy wzór na rozkład hipergeometryczny, zastępujemy zmienne odpowiadającymi im wartościami i wykonujemy obliczenia:

$P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}$

$\begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}$

Kalkulator rozkładu hipergeometrycznego

Wprowadź parametry rozkładu hipergeometrycznego do poniższego kalkulatora online, aby obliczyć prawdopodobieństwo wystąpienia pożądanego zdarzenia.

Pamiętaj, że N to wielkość populacji, K to całkowita liczba korzystnych przypadków, n to wielkość próby, a x to wartość, dla której chcemy znaleźć prawdopodobieństwo takiego zdarzenia.

Charakterystyka rozkładu hipergeometrycznego

Rozkład hipergeometryczny ma następujące właściwości:

Oczekiwana wartość rozkładu hipergeometrycznego jest równa liczbie elementów w próbie pomnożonej przez całkowitą liczbę korzystnych przypadków podzieloną przez liczbę elementów w populacji.

$E[X]=\cfrac{n\cdot K}{N}$

Tryb rozkładu hipergeometrycznego to wartość zaokrąglona w dół iloczynu n+1 razy K+1 podzielonego przez N+2 .

$\displaystyle M=\Bigg\lfloor \frac{(n+1)(K+1)}{N+2}\Bigg\rfloor$

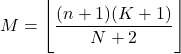
Wariancję rozkładu hipergeometrycznego można obliczyć za pomocą następującego wyrażenia:

$\displaystyle Var[X]=\cfrac{nK}{N}\left(\frac{N-K}{N}\right)\left(\frac{N-n}{N-1}\right)$

Funkcja generująca moment rozkładu hipergeometrycznego jest następująca:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K-n+1; e^{t}) } }{{N \choose n}}$

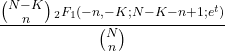
Charakterystyczna funkcja rozkładu hipergeometrycznego jest następująca:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K - n + 1; e^{it}) }}{{N \choose n}}$

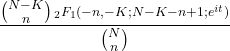
Prawdopodobieństwo wystąpienia danej liczby zdarzeń można obliczyć z prawdopodobieństwa liczby poprzedniej, stosując rekurencję dla rozkładu hipergeometrycznego:

$P[X=x+1]=\cfrac{(K-x)(n-x)}{(x+1)(N-K-n+x-1)}\cdot P[X=x]$

Rozkład hipergeometryczny i rozkład dwumianowy

Różnica między rozkładem hipergeometrycznym a rozkładem dwumianowym polega na zastąpieniu. Rozkład hipergeometryczny stosuje się, gdy wyszukiwania nie są zastępowane, natomiast w przypadku rozkładu dwumianowego zastępowane są wyszukiwania.

Na przykład, jeśli losujemy pięć kart w talii i chcemy obliczyć prawdopodobieństwo otrzymania określonej karty, jeśli nie będziemy wymieniać każdej dobieranej karty, do obliczeń musimy użyć rozkładu hipergeometrycznego. Jeśli jednak wyjmując kartę, odłożymy ją z powrotem przed wykonaniem kolejnej ekstrakcji, wówczas do obliczenia prawdopodobieństwa musimy skorzystać z rozkładu dwumianowego.

Gdy liczba N jest duża, stosunek n/N jest mały, a liczba pożądanych korzystnych przypadków jest bardzo mała, możemy zastosować rozkład hipergeometryczny jako przybliżenie rozkładu dwumianowego. Nie polecam jednak tego, gdyż wynik nie będzie tak wiarygodny, a ponadto łatwiej jest obliczyć prawdopodobieństwa z prawa dwumianu niż z prawa hipergeometrycznego.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej