Rozkład normalny

Rozkład normalny jest najczęstszym rozkładem prawdopodobieństwa w statystyce.

Rozkłady normalne mają następujące cechy:

• Kształt dzwonka
• Symetryczny
• Średnia i mediana są równe; oba znajdują się w centrum dystrybucji
• Około 68% danych mieści się w granicach jednego odchylenia standardowego średniej
• Około 95% danych mieści się w granicach dwóch odchyleń standardowych od średniej.
• Około 99,7% danych mieści się w granicach trzech odchyleń standardowych od średniej.

Ostatnie trzy punkty są znane jako praktyczna zasada , czasami nazywana zasadą 68-95-99,7 .

Powiązane: Praktyczna zasada (zagadnienia praktyczne)

Jak narysować krzywą normalną

Aby narysować krzywą normalną, musimy znać średnią i odchylenie standardowe.

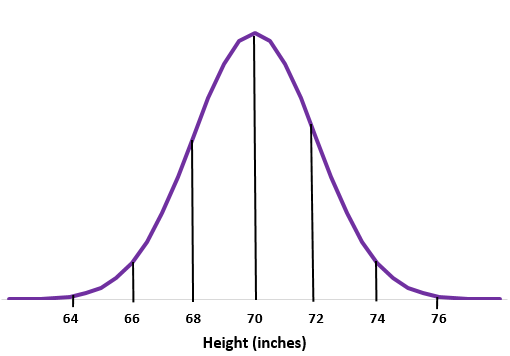
Przykład 1: Załóżmy, że wzrost mężczyzn w pewnej szkole ma rozkład normalny ze średnią $\mu =\; 70\; cali\; i$ odchyleniem standardowym $\sigma \; =\; 2\; cale.\; Naszkicuj\; krzywą\; normalną.$

Krok 1: Naszkicuj krzywą normalną.

Krok 2: Średnia 70 cali znajduje się pośrodku.

Krok 3: Każde odchylenie standardowe odpowiada odległości 2 cali.

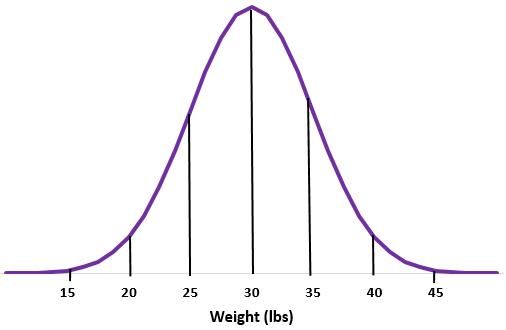
Przykład 2: Załóżmy, że masa pewnego gatunku wydry ma rozkład normalny ze średnią $\mu =\; 30\; funtów\; i$ odchyleniem standardowym $\sigma \; =\; 5\; funtów.\; Naszkicuj\; krzywą\; normalną.$

Krok 1: Naszkicuj krzywą normalną.

Krok 2: Średnia waga 30 funtów mieści się pośrodku.

Krok 3: Każde odchylenie standardowe odpowiada odległości 5 funtów

Jak znaleźć procenty za pomocą rozkładu normalnego

Praktyczna zasada , czasami nazywana regułą 68-95-99,7 , stwierdza, że dla zmiennej losowej o rozkładzie normalnym 68% danych mieści się w przedziale jednego odchylenia standardowego od średniej, a 95% mieści się w przedziale dwóch odchyleń standardowych odchylenia od średniej, a 99,7% mieści się w granicach trzech odchyleń standardowych od średniej.

Korzystając z tej reguły, możemy odpowiedzieć na pytania dotyczące procentów.

Przykład: Załóżmy, że wzrost mężczyzn w pewnej szkole ma rozkład normalny ze średnią $\mu =\; 70\; cali\; i$ odchyleniem standardowym $\sigma \; =\; 2\; cale.$

$Jaki\; procent\; mężczyzn\; w\; tej\; szkole\; ma\; w\; przybliżeniu\; ponad\; 74\; cale\; wzrostu?$

Rozwiązanie:

Krok 1: Naszkicuj rozkład normalny ze średnią $\mu =\; 70\; cali\; i$ odchyleniem standardowym $\sigma \; =\; 2\; cale.$

Krok 2: Wysokość 74 cali to dwa odchylenia standardowe powyżej średniej. Dodaj wartości procentowe powyżej tego punktu do rozkładu normalnego.

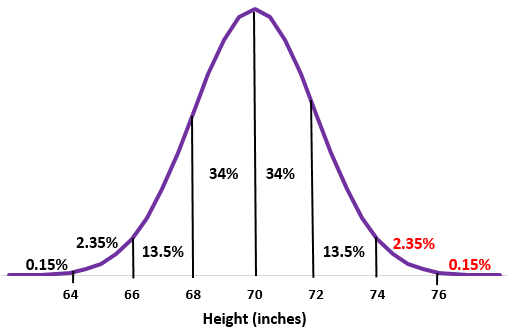
2,35% + 0,15% = 2,5%

Około 2,5% mężczyzn w tej szkole ma ponad 74 cale wzrostu.

$Jaki\; procent\; mężczyzn\; w\; tej\; szkole\; ma\; w\; przybliżeniu\; wzrost\; od\; 68\; do\; 72\; cali?$

Rozwiązanie:

Krok 1: Naszkicuj rozkład normalny ze średnią $\mu =\; 70\; cali\; i$ odchyleniem standardowym $\sigma \; =\; 2\; cale.$

Krok 2: Wysokość 68 cali i 72 cale to odpowiednio jedno odchylenie standardowe poniżej i powyżej średniej. Wystarczy dodać wartości procentowe pomiędzy tymi dwoma punktami rozkładu normalnego.

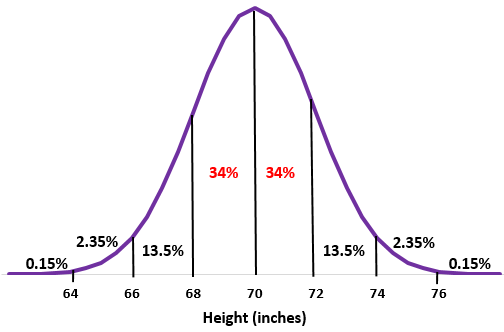
34% + 34% = 68%

Około 68% mężczyzn w tej szkole ma wzrost od 68 do 72 cali.

Jak znaleźć liczbę przy użyciu rozkładu normalnego

Możemy również zastosować praktyczną regułę, aby odpowiedzieć na pytania dotyczące liczebności.

Przykład: Załóżmy, że masa pewnego gatunku wydry ma rozkład normalny ze średnią $\mu =\; 30\; funtów\; i$ odchyleniem standardowym $\sigma \; =\; 5\; funtów.$

W pewnej kolonii jest 200 takich wydr. Ile w przybliżeniu tych wydr waży więcej niż 35 funtów?

Rozwiązanie:

Krok 1: Naszkicuj rozkład normalny ze średnią $\mu =\; 30\; funtów\; i$ odchyleniem standardowym $\sigma \; =\; 5\; funtów.$

Krok 2: Waga 35 funtów to jedno odchylenie standardowe powyżej średniej. Dodaj wartości procentowe powyżej tego punktu do rozkładu normalnego.

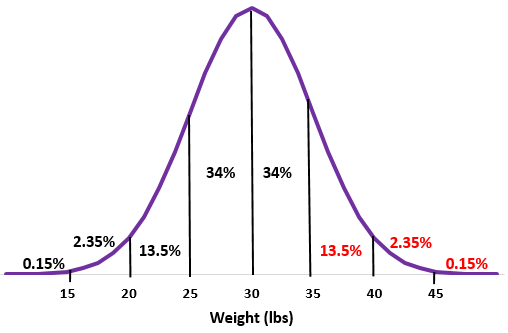
13,5% + 2,35% + 0,15% = 16%

Krok 3: Ponieważ w kolonii jest 200 wydr, 16% z 200 = 0,16 * 200 = 32

Około 32 wydr w tej kolonii waży ponad 35 funtów.

Ile w przybliżeniu wydr w tej kolonii waży mniej niż 30 funtów?

Zamiast wykonywać wszystkie kroki, które właśnie wykonaliśmy powyżej, możemy uznać, że mediana rozkładu normalnego jest równa średniej, która w tym przypadku wynosi 30 funtów.

Oznacza to, że połowa wydr waży ponad 30 funtów, a druga połowa mniej niż 30 funtów. Oznacza to, że 50% z 200 wydr waży mniej niż 30 funtów, więc 0,5 * 200 = 100 wydr .

Dodatkowe zasoby

Poniższe samouczki zawierają dodatkowe informacje na temat rozkładu normalnego:

6 konkretnych przykładów rozkładu normalnego
Rozkład normalny a rozkład t: różnica
Jak utworzyć krzywą dzwonową w programie Excel
Jak utworzyć krzywą dzwonową w Pythonie