Rozkład normalny lub równomierny: jaka jest różnica?

Rozkład normalny jest najczęściej używanym rozkładem prawdopodobieństwa w statystyce.

Posiada następujące właściwości:

• Symetryczny
• kształt dzwonu

Jeśli utworzymy wykres rozkładu normalnego, będzie on wyglądał następująco:

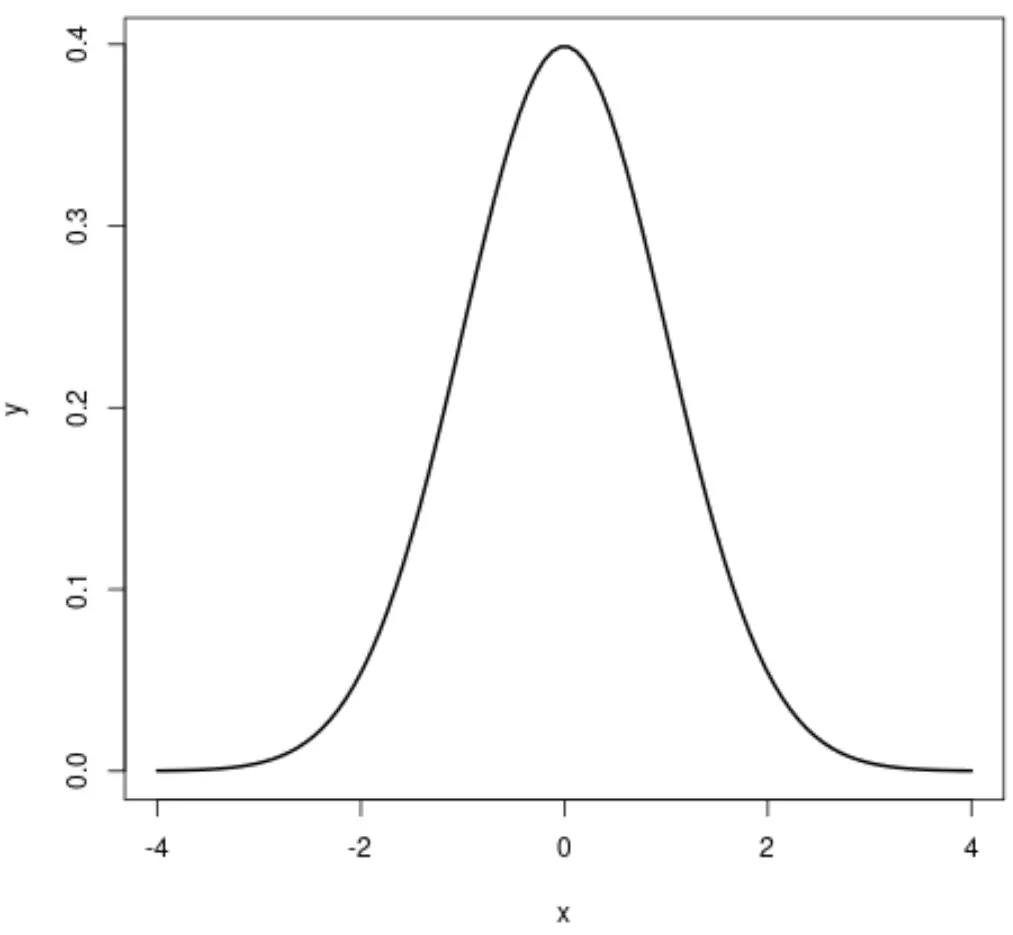
Rozkład równomierny to rozkład prawdopodobieństwa, w którym każda wartość w przedziale od a do b ma to samo prawdopodobieństwo wystąpienia.

Posiada następujące właściwości:

• Symetryczny
• Kształt prostokątny

Jeśli utworzymy wykres rozkładu równomiernego, będzie on wyglądał następująco:

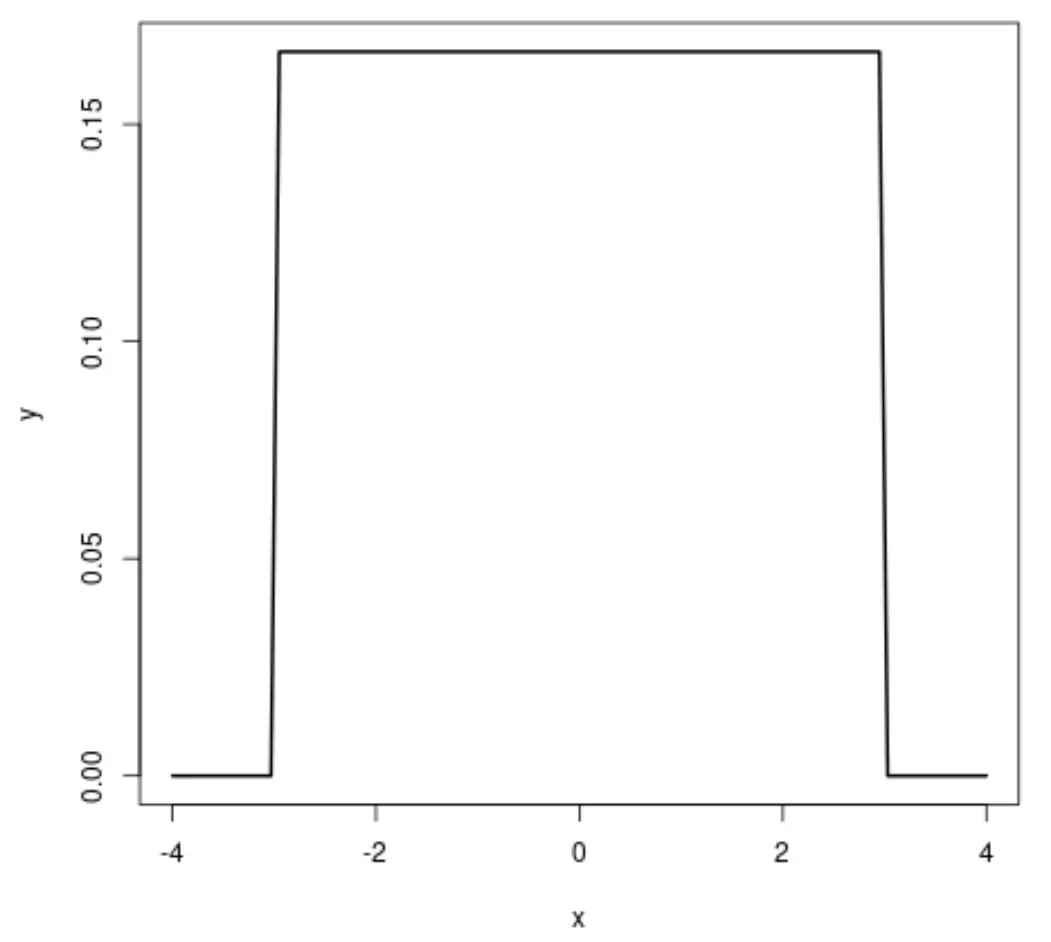
Rozkład normalny i rozkład równomierny mają następujące podobieństwo :

• Obydwa rozkłady są symetryczne. Oznacza to, że gdybyśmy narysowali linię przez środek rozkładu, lewa i prawa strona rozkładu idealnie by się odzwierciedlały:

Jednakże te dwie dystrybucje mają następującą różnicę :

• Dystrybucje mają różne kształty.
• Rozkład normalny ma kształt dzwonu, co oznacza, że wartości w pobliżu środka rozkładu są bardziej prawdopodobne niż wartości na końcach rozkładu.
• Rozkład równomierny ma kształt prostokątny, co oznacza, że każda wartość w rozkładzie ma takie samo prawdopodobieństwo wystąpienia.

Rozkład normalny czy rozkład równomierny: kiedy je stosować?

Rozkład normalny służy do modelowania zjawisk, które zwykle mają kształt „krzywej dzwonowej”. Na przykład dobrze udokumentowano, że masa urodzeniowa noworodków zwykle wynosi średnio około 7,5 funta.

Histogram masy urodzeniowej noworodków w Stanach Zjednoczonych ma kształt dzwonu, który ogólnie odpowiada rozkładowi normalnemu:

Większość dzieci prawdopodobnie waży około 7,5 funta, niektóre ważą mniej niż 7 funtów, a niektóre ważą ponad 8 funtów.

I odwrotnie, rozkład równomierny służy do modelowania scenariuszy, w których każdy potencjalny wynik jest równie prawdopodobny.

Klasycznym przykładem jest rzut kostką. Jeśli rzucisz raz kostką, prawdopodobieństwo, że wypadnie ona na liczbę od 1 do 6, ma rozkład równomierny, ponieważ prawdopodobieństwo pojawienia się każdej liczby jest takie samo.

Na przykład istnieje 6 możliwych liczb, na których może wylądować kość, więc prawdopodobieństwo, że wyrzucisz 1, wynosi 1/6.

Podobnie prawdopodobieństwo, że wyrzucisz 2, wynosi 1/6.

Podobnie prawdopodobieństwo, że wyrzucisz 3, wynosi 1/6.

I tak dalej.

Bonus: Jak wykreślić rozkład normalny i równomierny

Użyliśmy następującego kodu w R, aby utworzyć wykresy rozkładu normalnego i jednorodnego:

 #define x-axis
x <- seq(-4, 4, length=100)

#calculate normal distribution probabilities
y <- dnorm(x)

#plot normal distribution
plot(x, y, type = " l ", lwd = 2 )

#define x-axis
x <- seq(-4, 4, length=100)

#calculate uniform distribution probabilities
y <- dunif(x, min = -3, max = 3)

#plot uniform distribution
plot(x, y, type = " l ", lwd = 2 , xlim = c(-4, 4))

Dodatkowe zasoby

6 konkretnych przykładów rozkładu normalnego
5 konkretnych przykładów równomiernego rozkładu
Rozkład symetryczny: definicja + przykłady