Rozkład normalny i rozkład t: jaka jest różnica?

Rozkład normalny jest najczęściej używanym rozkładem we wszystkich statystykach i wiadomo, że jest symetryczny i ma kształt dzwonu.

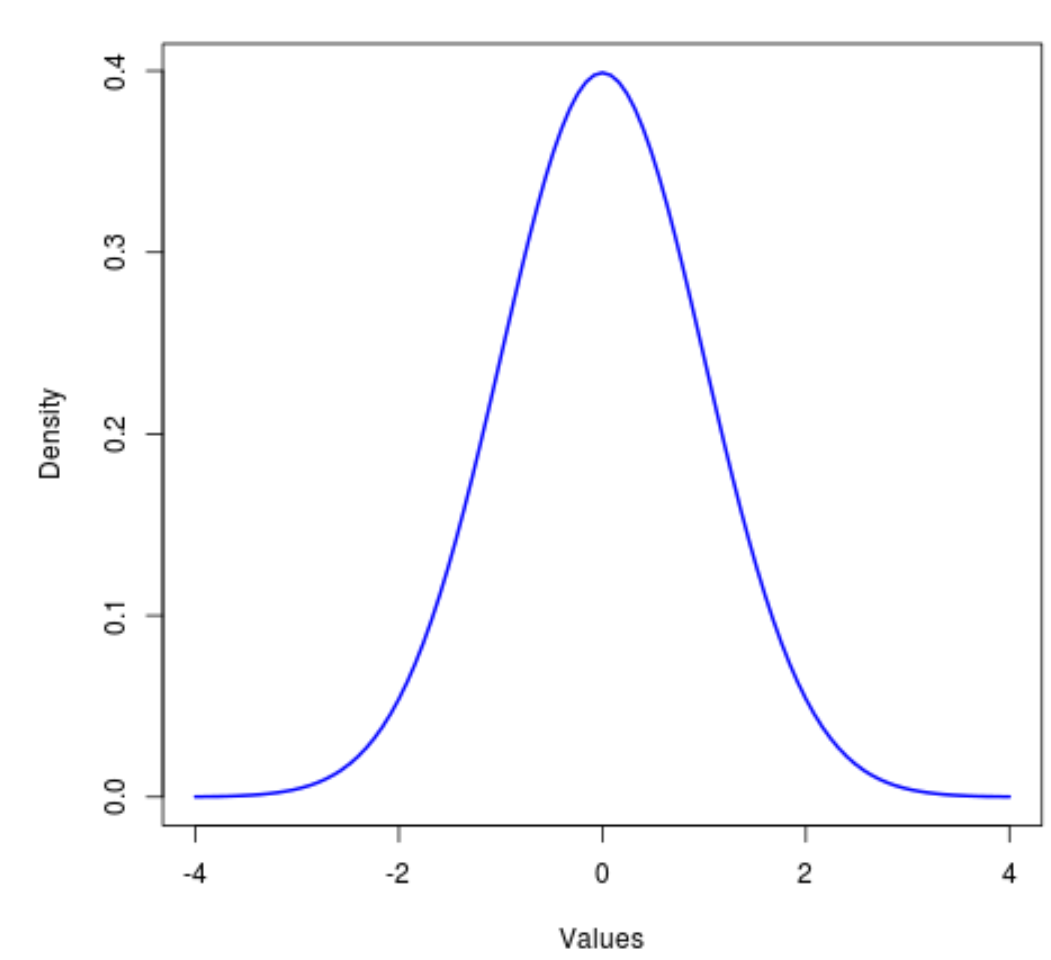
Ściśle powiązanym rozkładem jest rozkład t , który również jest symetryczny i ma kształt dzwonu, ale ma cięższe „ogony” niż rozkład normalny.

Inaczej mówiąc, więcej wartości w rozkładzie znajduje się na końcach niż w środku w porównaniu do rozkładu normalnego:

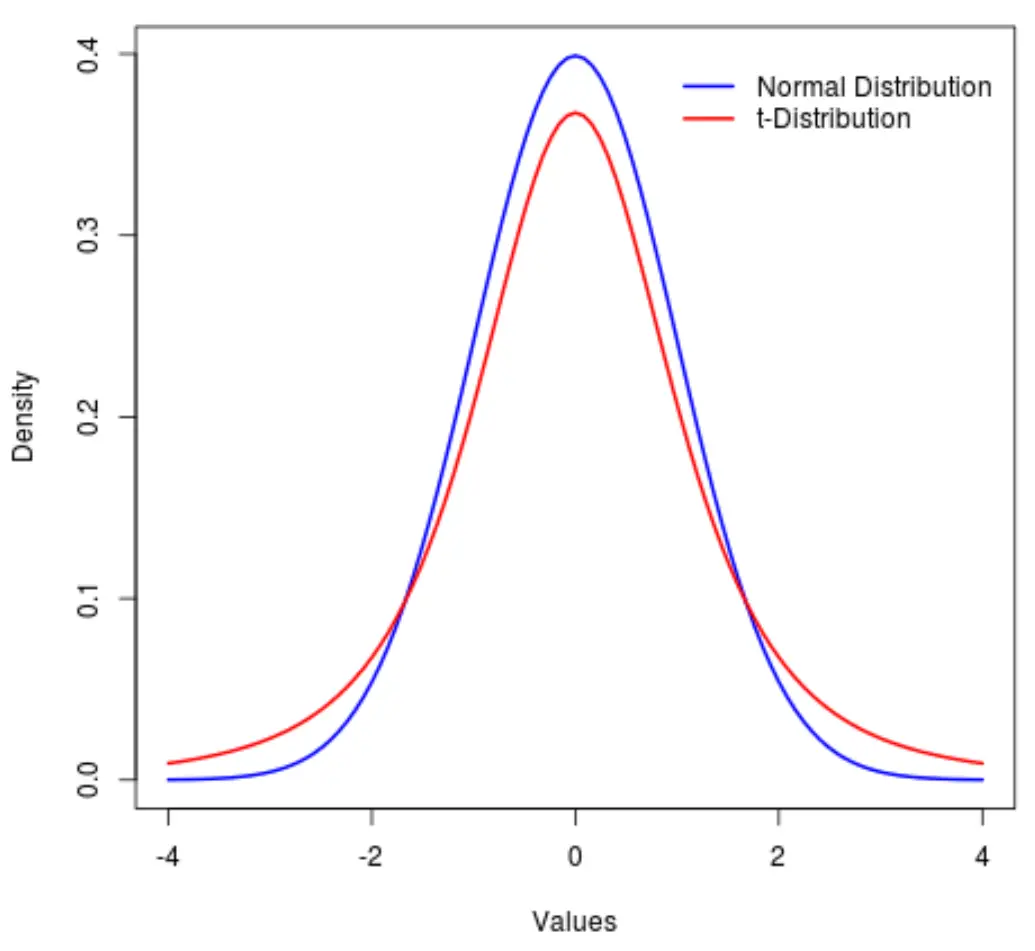
W żargonie statystycznym używamy metryki zwanej kurtozą , aby zmierzyć, jak „ciężki” jest rozkład. Powiedzielibyśmy więc, że kurtoza rozkładu t jest większa niż kurtoza rozkładu normalnego.

W praktyce rozkładu t używamy najczęściej przytestowaniu hipotez lub konstruowaniu przedziałów ufności .

Na przykład wzór na obliczenie przedziału ufności dla średniej populacji wygląda następująco:

Przedział ufności = x +/- t _{1-α/2, n-1} *(s/√ n )

Złoto:

• x : przykładowe środki
• t: krytyczna wartość t, oparta na poziomie istotności α i wielkości próby n
• s: odchylenie standardowe próbki
• n: wielkość próbki

W tym wzorze używamy wartości krytycznej tabeli t zamiast wartości krytycznej tabeli z, gdy spełniony jest jeden z następujących warunków:

• Nie znamy odchylenia standardowego populacji.
• Wielkość próby jest mniejsza lub równa 30.

Poniższy schemat blokowy pozwala w przydatny sposób dowiedzieć się, czy należy użyć wartości krytycznej z tabeli t, czy z tabeli z:

Główna różnica między wykorzystaniem rozkładu t a wykorzystaniem rozkładu normalnego przy konstruowaniu przedziałów ufności polega na tym, że wartości krytyczne rozkładu t będą większe, co prowadzi do szerszych przedziałów ufności.

Załóżmy na przykład, że chcemy skonstruować 95% przedział ufności dla średniej masy populacji żółwi, aby zebrać losową próbkę żółwi zawierającą następujące informacje:

• Wielkość próby n = 25
• Średnia masa próbki x = 300
• Próbka odchylenie standardowe s = 18,5

Krytyczna wartość z dla 95% poziomu ufności wynosi 1,96 , podczas gdy krytyczna wartość t dla 95% przedziału ufności z df = 25-1 = 24 stopniami swobody wynosi 2,0639 .

Zatem 95% przedział ufności dla średniej populacji przy użyciu wartości krytycznej z wynosi:

95% CI = 300 +/- 1,96*(18,5/√ 25 ) = [292,75, 307,25]

Podczas gdy 95% przedział ufności dla średniej populacji przy użyciu wartości krytycznej t wynosi:

95% CI = 300 +/- 2,0639*(18,5/√25) = [292,36, 307,64]

Należy zauważyć, że przedział ufności z wartością krytyczną t jest szerszy.

Pomysł jest taki, że gdy mamy małe próby, nie jesteśmy pewni prawdziwej średniej populacji, dlatego przydatne jest użycie rozkładu t w celu uzyskania szerszych przedziałów ufności, które mają większe szanse na uwzględnienie prawdziwej średniej populacji.

Wizualizacja stopni swobody dla rozkładu t

Należy zauważyć, że wraz ze wzrostem stopni swobody rozkład t zbliża się do rozkładu normalnego.

Aby to zilustrować, rozważ poniższy wykres przedstawiający kształt rozkładu t z następującymi stopniami swobody:

• df = 3
• df = 10
• df = 30

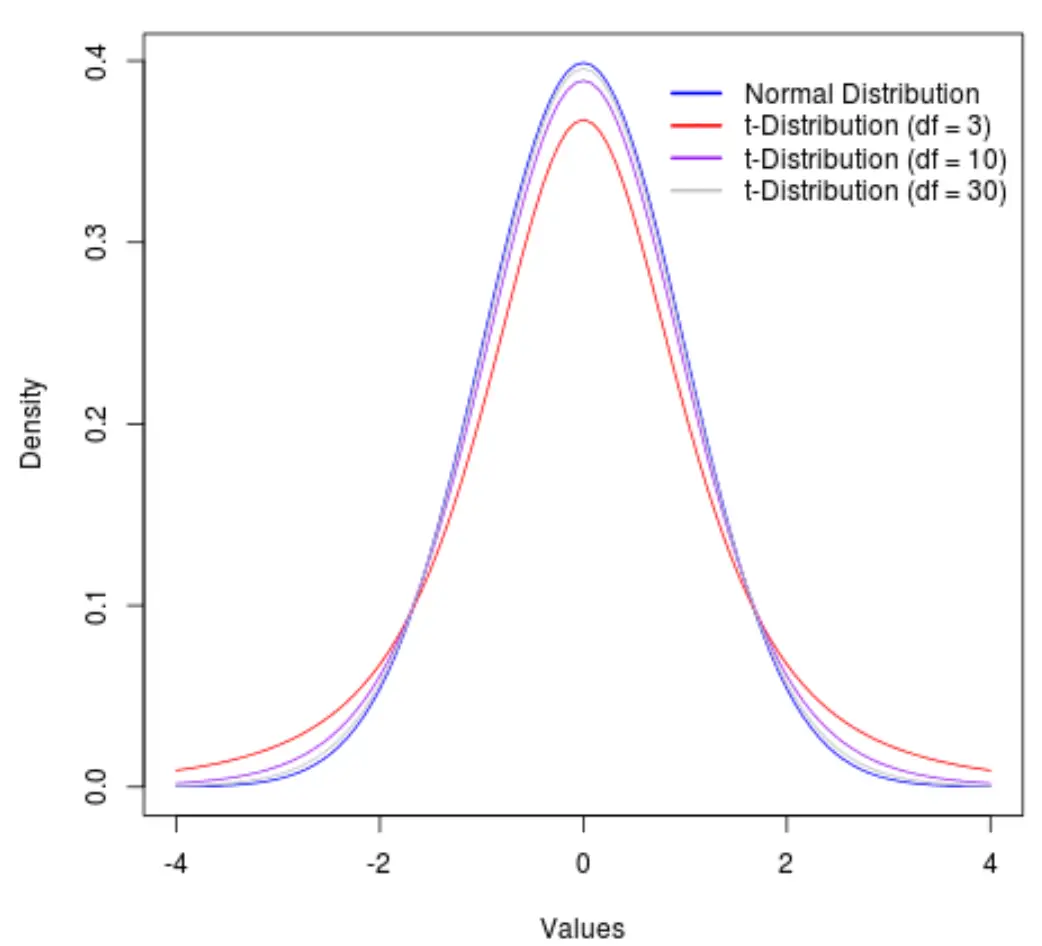
Powyżej 30 stopni swobody rozkład t i rozkład normalny stają się tak podobne, że różnice między użyciem we wzorach wartości krytycznej t i wartości krytycznej z stają się pomijalne.