Rozkład normalny i standardowy rozkład normalny: różnica

Rozkład normalny jest najczęściej używanym rozkładem prawdopodobieństwa w statystyce.

Ma następujące właściwości:

• Symetryczny
• kształt dzwonu
• Średnia i mediana są równe; oba zlokalizowane w centrum dystrybucji

Średnia rozkładu normalnego określa jego położenie, a odchylenie standardowe określa jego rozproszenie.

Na przykład poniższy wykres przedstawia trzy rozkłady normalne z różnymi średnimi i odchyleniami standardowymi:

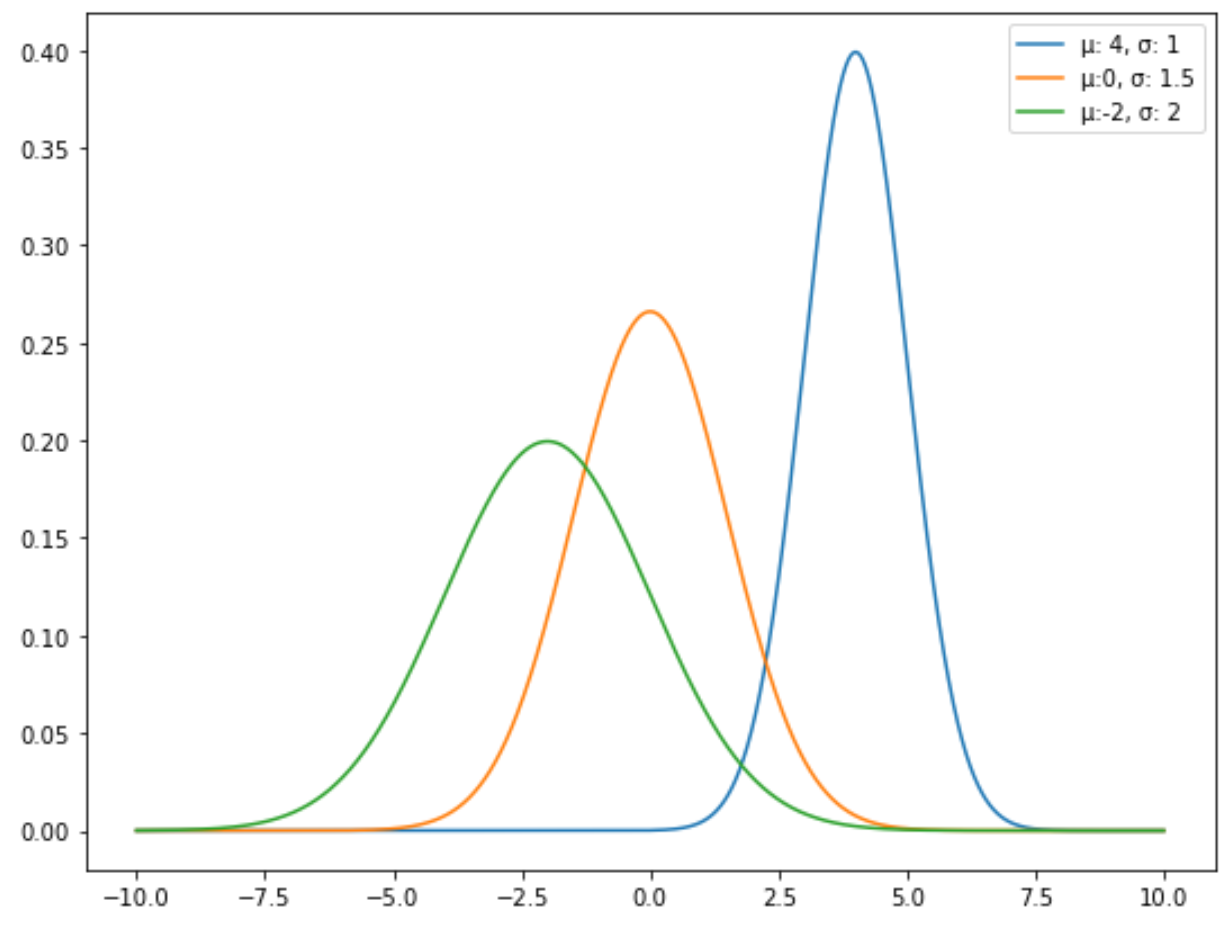
Standardowy rozkład normalny to specyficzny typ rozkładu normalnego, w którym średnia wynosi 0, a odchylenie standardowe wynosi 1.

Poniższy wykres przedstawia standardowy rozkład normalny:

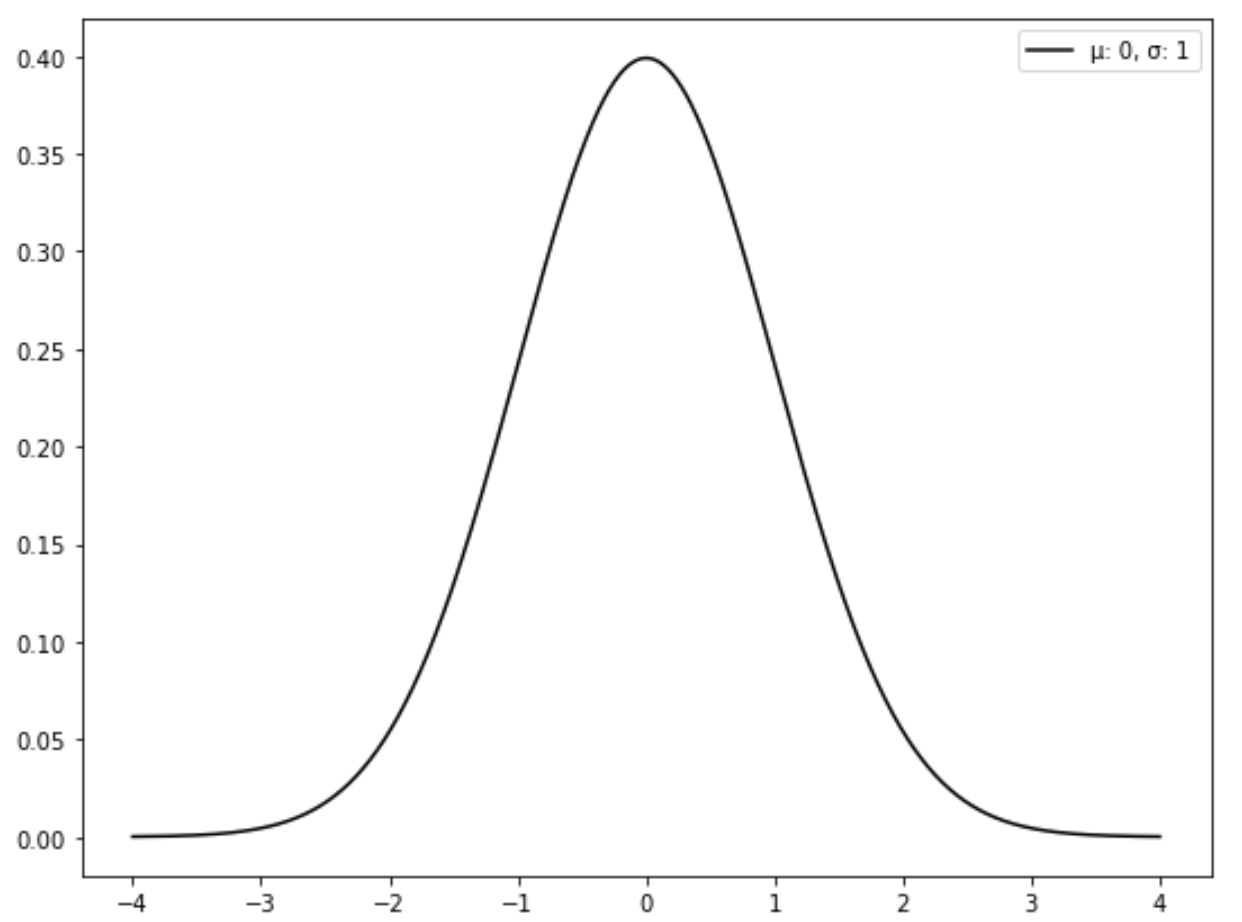
Jak zamienić rozkład normalny na standardowy rozkład normalny

Każdy rozkład normalny można przekształcić w standardowy rozkład normalny, konwertując wartości danych na współczynniki Z, korzystając z następującego wzoru:

z = (x – μ) / σ

Złoto:

• x: wartość poszczególnych danych
• μ: średnia rozkładu
• σ: Odchylenie standardowe rozkładu

Załóżmy na przykład, że mamy następujący zestaw danych ze średnią 6 i odchyleniem standardowym 2,152:

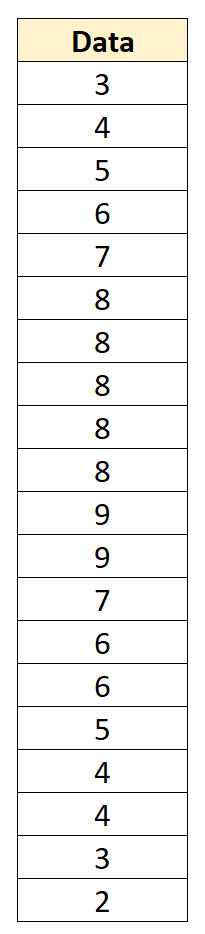
Możemy przekonwertować każdą indywidualną wartość danych na wynik z, odejmując 6 od każdej wartości i dzieląc przez 2,152:

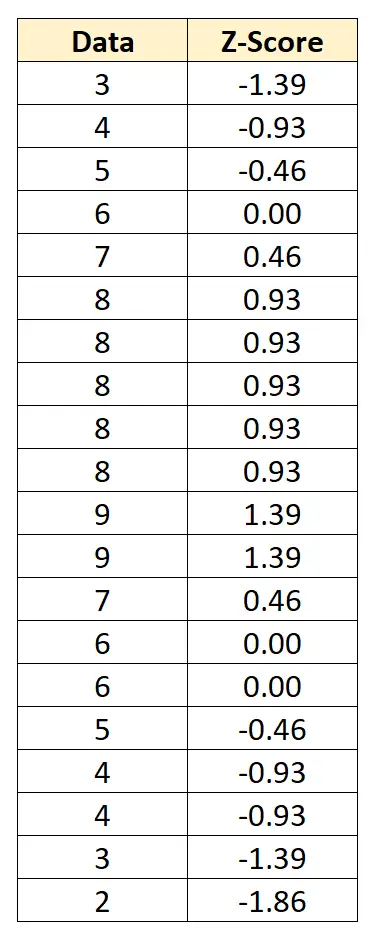
Wynik z mówi nam, o ile odchyleń standardowych każdy punkt danych różni się od średniej. Na przykład pierwsza wartość danych „3” wynosi 1,39 odchylenia standardowego poniżej średniej.

Średnia tego rozkładu wyników ma średnią wynoszącą zero i odchylenie standardowe wynoszące jeden.

Jak korzystać ze standardowego rozkładu normalnego

Standardowy rozkład normalny ma następujące właściwości:

• Około 68% danych mieści się w granicach jednego odchylenia standardowego średniej
• Około 95% danych mieści się w granicach dwóch odchyleń standardowych od średniej.
• Około 99,7% danych mieści się w granicach trzech odchyleń standardowych od średniej.

Jest to znana praktyczna zasada i służy do zrozumienia rozkładu wartości w zbiorze danych.

Załóżmy na przykład, że wysokość roślin w pewnym ogrodzie ma rozkład normalny, a średnia wynosi 47,4 cala i odchylenie standardowe wynosi 2,4 cala.

Stosując praktyczną zasadę, jaki procent roślin ma wysokość mniejszą niż 150 cm?

Praktyczna zasada mówi, że dla danego zbioru danych o rozkładzie normalnym 99,7% wartości danych mieści się w granicach trzech odchyleń standardowych od średniej. Oznacza to, że 49,85% wartości mieści się pomiędzy średnią a trzema odchyleniami standardowymi powyżej średniej.

W tym przykładzie 54,6 to trzy odchylenia standardowe powyżej średniej. Ponieważ wiemy, że 50% wartości danych jest mniejszych niż średnia w rozkładzie normalnym, łącznie 50% + 49,85% = 99,85% wartości jest mniejszych niż 54,6.

Zatem 99,85% roślin ma wysokość mniejszą niż 150 cm.

Dodatkowe zasoby

Problemy w praktyce praktycznych zasad
Zasady kalkulatora kciuka
Jak zastosować regułę praktyczną w programie Excel