Jak obliczyć rozkłady próbkowania w programie excel

Rozkład próbkowania to rozkład prawdopodobieństwa określonej statystyki oparty na wielu losowych próbach z jednej populacji .

W tym samouczku wyjaśniono, jak wykonać następujące czynności z rozkładami próbkowania w programie Excel:

• Wygeneruj rozkład próbkowania.
• Wizualizuj rozkład próbkowania.
• Oblicz średnią i odchylenie standardowe rozkładu próbkowania.
• Oblicz prawdopodobieństwa dotyczące rozkładu próby.

Wygeneruj rozkład próbkowania w programie Excel

Załóżmy, że chcemy wygenerować rozkład próbkowania składający się z 1000 próbek, w którym wielkość każdej próbki wynosi 20 i pochodzi z rozkładu normalnego ze średnią 5,3 i odchyleniem standardowym 9 .

Możemy to łatwo zrobić wpisując w komórkę A2 naszego arkusza kalkulacyjnego następującą formułę:

 = NORM . INV ( RAND (), 5.3, 9)

Możemy następnie najechać kursorem na prawy dolny róg komórki, aż pojawi się mały + i przeciągnąć formułę do 20 komórek w prawo i 1000 komórek w dół:

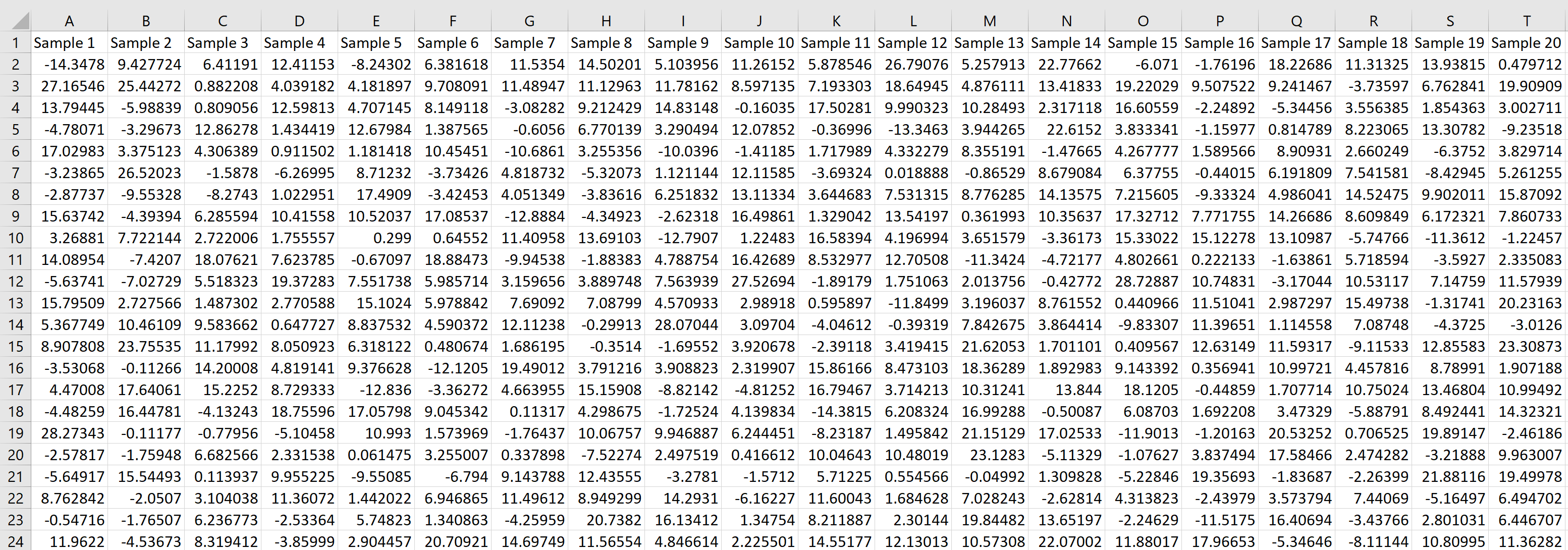
Każdy wiersz reprezentuje próbkę o wielkości 20, w której każda wartość pochodzi z rozkładu normalnego ze średnią 5,3 i odchyleniem standardowym 9.

Znajdź średnią i odchylenie standardowe

Aby znaleźć średnią i odchylenie standardowe tego rozkładu próbkowania średnich z próbek, możemy najpierw znaleźć średnią każdej próbki, wpisując następującą formułę do komórki U2 naszego arkusza:

 = AVERAGE (A2:T2)

Możemy następnie najechać kursorem na prawy dolny róg komórki, aż pojawi się mały + i kliknąć dwukrotnie, aby skopiować tę formułę do wszystkich pozostałych komórek w kolumnie U:

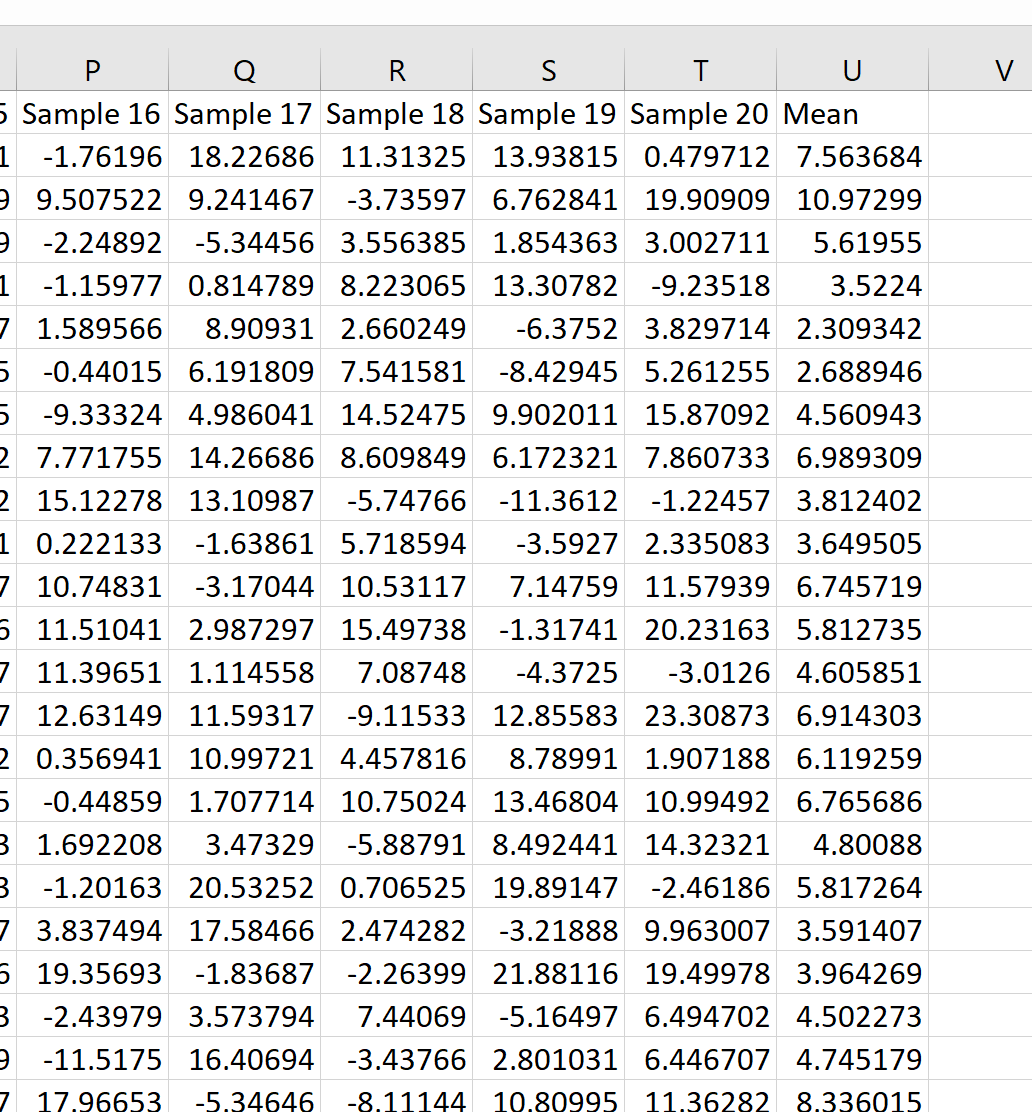
Widzimy, że pierwsza próbka miała średnią 7,563684, druga próbka miała średnią 10,97299 i tak dalej.

Następnie możemy użyć następujących wzorów do obliczenia średniej i odchylenia standardowego średnich z próbki:

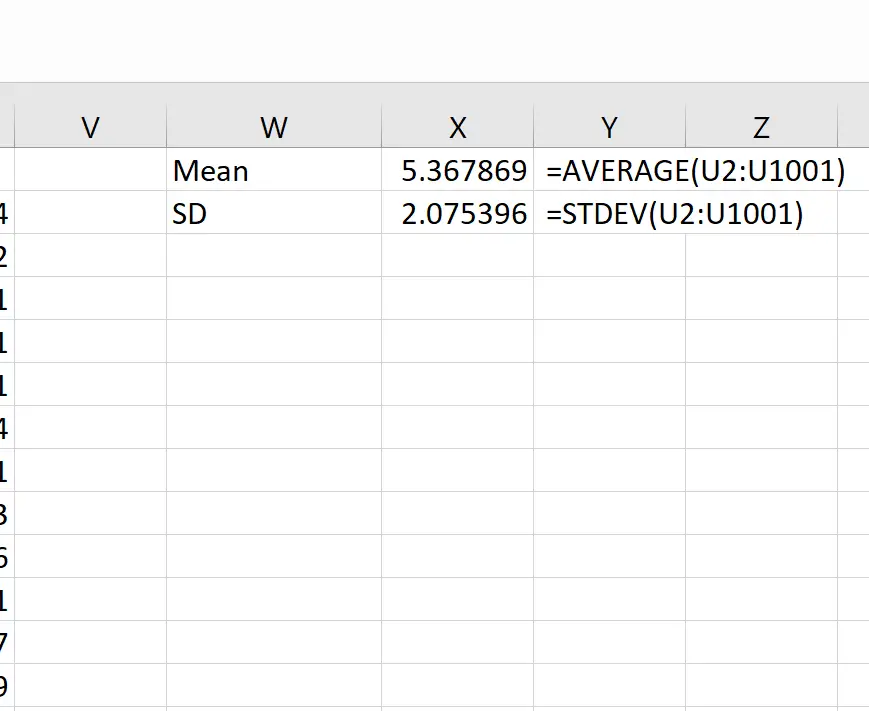
Teoretycznie średnia rozkładu próby powinna wynosić 5,3. Widzimy, że rzeczywista średnia z próbki w tym przykładzie wynosi 5,367869 , czyli blisko 5,3.

Teoretycznie odchylenie standardowe rozkładu próbkowania powinno być równe s/√n, czyli 9 / √20 = 2,012. Widzimy, że rzeczywiste odchylenie standardowe rozkładu próbkowania wynosi 2,075396 , co jest bliskie 2,012.

Wizualizuj rozkład próbkowania

Możemy również utworzyć prosty histogram do wizualizacji rozkładu próbkowania średnich z próbki.

Aby to zrobić, po prostu zaznacz wszystkie średnie próbki w kolumnie U, kliknij kartę Wstaw , a następnie kliknij opcję Histogram w sekcji Wykresy .

Daje to następujący histogram:

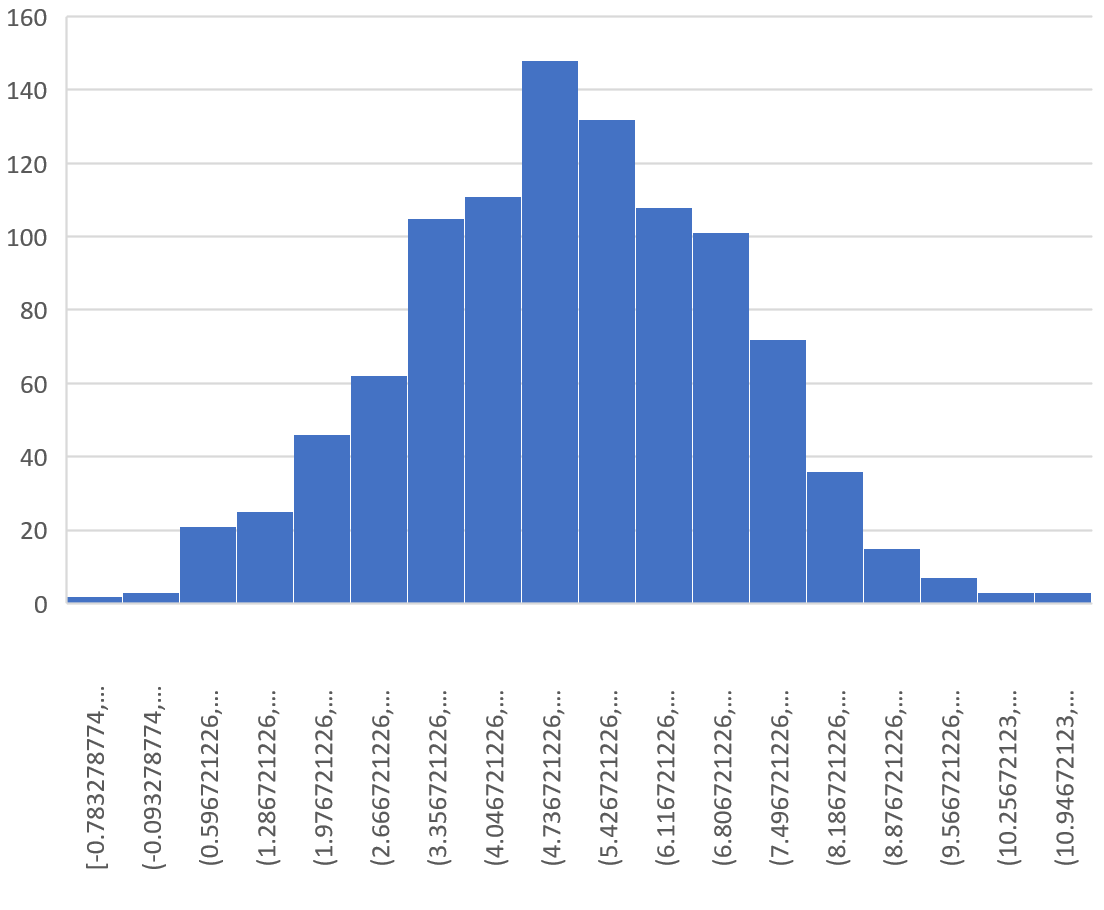
Można zauważyć, że rozkład próbkowania ma kształt dzwonu z pikiem w pobliżu wartości 5.

Jednak z ogonów rozkładu widać, że niektóre próbki miały średnie większe niż 10, a inne miały średnie mniejsze niż 0.

Oblicz prawdopodobieństwa

Możemy również obliczyć prawdopodobieństwo uzyskania określonej wartości średniej próbki na podstawie średniej populacji, odchylenia standardowego populacji i wielkości próby.

Na przykład możemy użyć poniższego wzoru, aby znaleźć prawdopodobieństwo, że średnia próbki jest mniejsza lub równa 6, przy założeniu, że średnia populacji wynosi 5,3, odchylenie standardowe populacji wynosi 9, a wielkość próby wynosi:

 = COUNTIF (U2:U1001, " <=6 ")/ COUNT (U2:U1001)

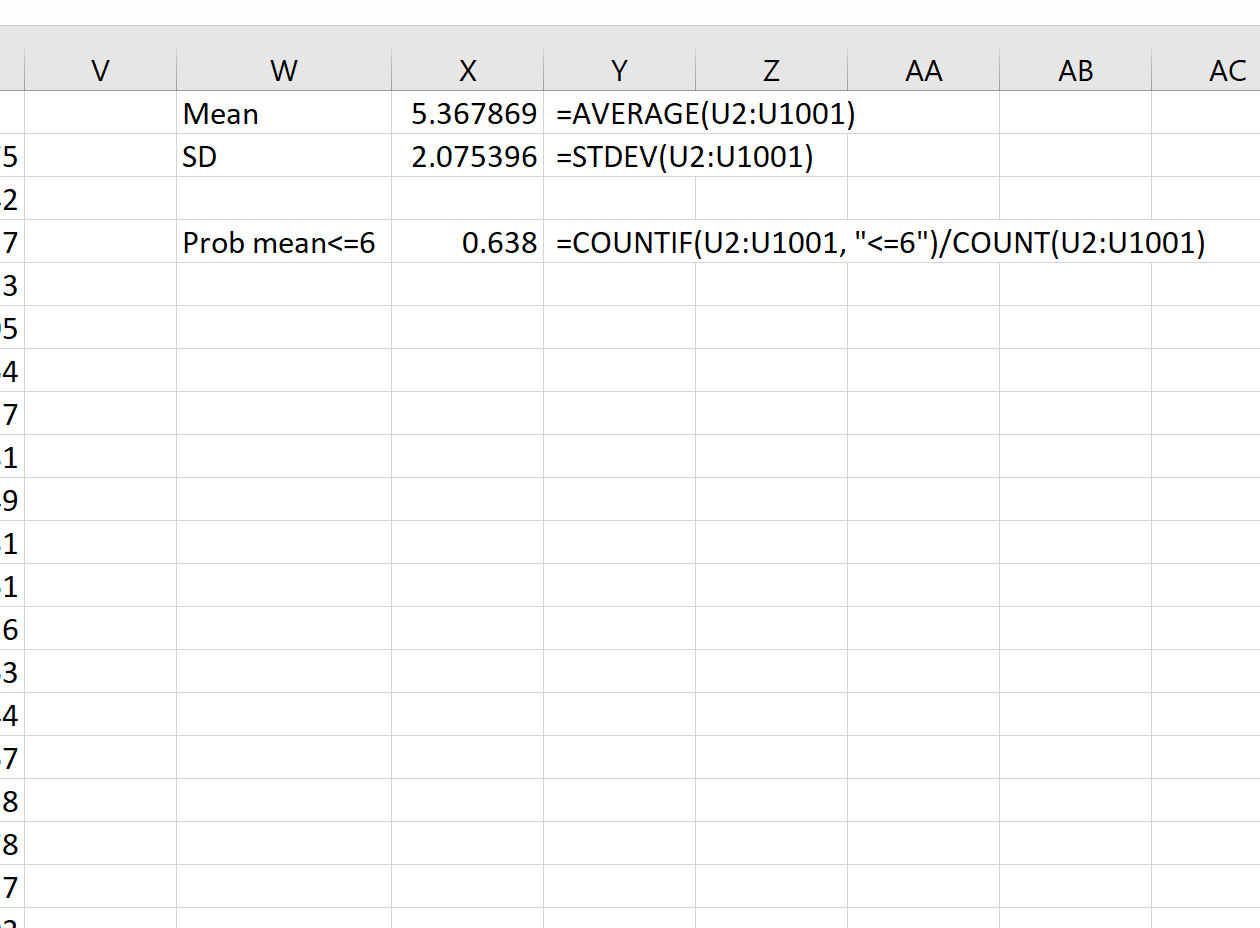
Widzimy, że prawdopodobieństwo, że średnia próbki jest mniejsza lub równa 6, wynosi 0,638.

Jest to bardzo zbliżone do prawdopodobieństwa obliczonego przez kalkulator rozkładu próbkowania :

Dodatkowe zasoby

Wprowadzenie do rozkładów próbkowania
Kalkulator rozkładu próbkowania
Wprowadzenie do centralnego twierdzenia granicznego