Próbkowanie rozkładu różnicy proporcji
W artykule wyjaśniono, na czym polega różnica w proporcjonalnym rozkładzie próbkowania i do czego służy w statystyce. Zaprezentowano także wzór na różnicę w proporcjach rozkładu próbkowania oraz krok po kroku rozwiązane ćwiczenie.
Jaki jest rozkład próbkowania różnicy proporcji?
Różnica w proporcjach rozkładu próbkowania to rozkład wynikający z obliczenia różnic pomiędzy proporcjami próbkowania wszystkich możliwych próbek z dwóch różnych populacji.
Oznacza to, że proces uzyskiwania rozkładu próbkowania różnicy proporcji polega, po pierwsze, na wyodrębnieniu wszystkich możliwych próbek z dwóch różnych populacji, po drugie, na określeniu proporcji każdej wyodrębnionej próbki, i wreszcie na określeniu różnicy pomiędzy wszystkimi proporcje różnicy proporcji. dwie populacje. Tak, że zbiór wyników uzyskanych po wykonaniu tych operacji tworzy rozkład próbkowania różnicy proporcji.

W statystyce różnica w proporcjach rozkładu próbkowania służy do obliczenia prawdopodobieństwa, że różnica między proporcjami dwóch losowo wybranych próbek będzie bliska różnicy w proporcjach populacji.
Wzór na rozkład różnicy proporcji w próbce
Próbki wybrane ze względu na różnicę proporcji rozkładu próbkowania są definiowane przez rozkłady dwumianowe , ponieważ dla celów praktycznych proporcja jest stosunkiem przypadków pomyślnych do całkowitej liczby obserwacji.
Niemniej jednak, dzięki centralnemu twierdzeniu granicznemu, rozkłady dwumianowe można przybliżyć do normalnych rozkładów prawdopodobieństwa . Dlatego rozkład próbkowania różnicy proporcji można przybliżyć do rozkładu normalnego o następujących cechach:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a1ce359b5dd6d80f8d27b0b9a1034bed_l3.png)
Uwaga: Rozkład próbkowania różnicy proporcji można przybliżyć do rozkładu normalnego tylko wtedy, gdy:
![]()
,
![]()
,
![]()
,
![]()
,
![]()
I
![]()
.
Ponieważ zatem rozkład próbkowania różnicy proporcji można przybliżyć do rozkładu normalnego, wzór na obliczenie statystyki rozkładu próbkowania różnicy proporcji jest następujący:

Złoto:
-

jest proporcją próbki, tj.
-

to odsetek populacji, tj.
-

jest prawdopodobieństwem niepowodzenia populacji i,

.
-

to wielkość próbki, tj.
-

jest zmienną zdefiniowaną przez standardowy rozkład normalny N(0,1).
Wzór ten jest podobny do wzoru na testowanie hipotezy na różnicę proporcji.
Konkretny przykład rozkładu próbkowania różnicy proporcji
Po zapoznaniu się z definicją różnicy proporcji rozkładu próbkowania i jej wzorem, możesz zobaczyć poniżej rozwiązany przykład krok po kroku, aby zakończyć zrozumienie koncepcji.
- Chcesz przeanalizować dokładność dwóch zakładów produkcyjnych, jedna fabryka produkuje w taki sposób, że tylko 5% wyprodukowanych części ma wady, podczas gdy w innej fabryce odsetek wadliwych części wynosi 8%. Jeśli weźmiemy próbkę 200 części z pierwszej fabryki i kolejną próbkę 280 części z drugiej fabryki, jakie jest prawdopodobieństwo, że procent defektów w pierwszym zakładzie produkcyjnym będzie większy niż procent defektów w drugiej fabryce? produkcja?
Aby zakończyć poznanie wszystkich danych problemu, najpierw obliczymy proporcję dobrze wyprodukowanych części każdej rośliny:
![Rendered by QuickLaTeX.com \begin{array}{c}q_1=1-p_1=1-0,05=0,95\\[2ex]q_2=1-p_2=1-0,08=0,92\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7c02732cc5fb319bfa5bf7b8ed8d03db_l3.png)
Jeżeli wskaźnik defektów w pierwszej fabryce był większy niż współczynnik defektów w drugiej fabryce, oznacza to, że prawdziwe byłoby następujące równanie:
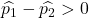
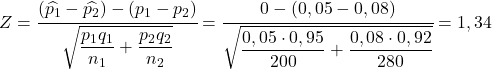
Zatem prawdopodobieństwo, że współczynnik defektów w pierwszej fabryce jest większy niż współczynnik defektów w drugiej fabryce, jest równoważne prawdopodobieństwu, że zmienna Z jest większa niż 1,34:
![P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”242″ style=”vertical-align: -5px;”></p>
</p>
<p> Na koniec wystarczy poszukać odpowiedniego prawdopodobieństwa w <a href=](https://statorials.org/wp-content/ql-cache/quicklatex.com-41dd897cdff473ff488cde0e3cc140b0_l3.png) tabeli rozkładu normalnego i już rozwiązaliśmy problem:
tabeli rozkładu normalnego i już rozwiązaliśmy problem:
![P[(\widehat{p_1}-\widehat{p_2})>0]=P[Z>1,34]=0,0901″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”319″ style=”vertical-align: -5px;”></p>
</p>
<p> Krótko mówiąc, prawdopodobieństwo, że odsetek wad w pierwszej fabryce będzie większy niż odsetek wad w drugiej fabryce, wynosi 9,01%. </p>
<div style=](https://statorials.org/wp-content/ql-cache/quicklatex.com-8d6e503a2089d30be8fd68bbc722bb44_l3.png) ➤ Zobacz: Próbkowanie rozkładu różnicy średnich
➤ Zobacz: Próbkowanie rozkładu różnicy średnich