Próbkowanie rozkładu różnicy średnich
W tym artykule wyjaśniono, jaki jest rozkład próbkowania różnicy między dwoma średnimi w statystyce. Znajdziesz tu także wzór na rozkład próbkowania różnicy średnich oraz dodatkowo rozwiązane ćwiczenie krok po kroku.
Jaki jest rozkład próbkowania różnicy średnich?
Rozkład próbkowania różnicy średnich to rozkład wynikający z obliczenia różnic między średnimi wszystkich możliwych próbek z dwóch różnych populacji.
Oznacza to, że aby otrzymać rozkład różnicy średnich w próbce, należy wybrać wszystkie możliwe próbki z dwóch populacji objętych badaniem, następnie obliczyć średnią z każdej wybranej próby i na koniec różnicę pomiędzy wszystkimi średnimi obliczonymi z dwóch populacji. Zatem zbiór wartości uzyskanych po zastosowaniu wszystkich tych operacji tworzy rozkład próbkowania różnicy średnich.

Różnicę rozkładu średnich prób wykorzystuje się do obliczenia prawdopodobieństwa, że różnica między dwiema średnimi losowo wybranymi próbami z dwóch różnych populacji będzie bliska różnicy średnich populacji.
Wzór na rozkład próbkowania różnicy średnich
Jeżeli wielkość próby jest wystarczająco duża (n 1 ≥30 i n 2 ≥30), rozkład różnicy średnich w próbce jest zgodny z rozkładem normalnym. Dokładniej, parametry wspomnianego rozkładu oblicza się w następujący sposób:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-90c67b74b4e9326b7869d641a59725d9_l3.png)
Uwaga: Jeśli obie populacje mają rozkłady normalne , wówczas rozkład różnicy średnich w próbce jest zgodny z rozkładem normalnym niezależnie od wielkości próby.
Dlatego też, ponieważ rozkład próbkowania różnicy średnich jest określony przez rozkład normalny, wzór na obliczenie statystyki rozkładu próbkowania różnicy średnich jest następujący:

Złoto:
-

jest średnią próbki i.
-

jest średnią populacji, tj.
-

jest odchyleniem standardowym populacji, tj.
-

to wielkość próbki, tj.
-

jest zmienną zdefiniowaną przez standardowy rozkład normalny N(0,1).
Należy pamiętać, że próbki z różnych populacji mogą mieć różną wielkość próby.
Konkretny przykład rozkładu próbkowania różnicy średnich
Kiedy już zapoznamy się z definicją różnicy rozkładu średnich prób i jaki jest jej wzór, zobaczymy przykład krok po kroku, aby zakończyć zrozumienie pojęcia różnicy rozkładu średnich próbkowania.
- W badaniu statystycznym chcemy przeanalizować różnicę między wzrostem chłopców i dziewcząt w określonym wieku. Wiemy, że rozkład określający populację chłopców w tym wieku ma średnią 157 cm i odchylenie standardowe 9 cm, natomiast rozkład określający populację dziewcząt w tym wieku ma średnią 148 cm cm i odchylenie standardowe 7 cm. Jeśli wybrano próbę 30 chłopców w tym wieku i próbę 35 dziewcząt w tym wieku, jakie jest prawdopodobieństwo, że średni wzrost w próbie chłopców jest o 12 cm większy od średniego wzrostu w próbie dziewcząt?
Aby rozwiązać ten problem, pierwszą rzeczą do zrobienia jest obliczenie statystyki różnicy średnich rozkładu próbkowania. Stosujemy zatem wzór przedstawiony powyżej:
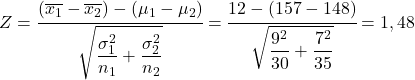
Zatem prawdopodobieństwo, że średni wzrost chłopców w próbie jest o 12 cm większy od średniego wzrostu dziewcząt, jest równoważne prawdopodobieństwu, że zmienna Z jest większa niż 1,48.
![P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”253″ style=”vertical-align: -5px;”></p>
</p>
<p> Dlatego szukamy prawdopodobieństwa Z>1,48 w <a href=](https://statorials.org/wp-content/ql-cache/quicklatex.com-683cd2a72980115d8d18c906d619370a_l3.png) tabeli Z :
tabeli Z :
![P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]=0,0694″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”331″ style=”vertical-align: -5px;”></p>
</p>
<p> Krótko mówiąc, prawdopodobieństwo, że średni wzrost chłopców w próbie jest o 12 cm większy od średniego wzrostu dziewcząt, wynosi 6,94%.</p>
</div><!-- End Content -->
<!-- Start Author Box -->
<div class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-5b83fdc11bd2320249679c4752660451_l3.png)
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej