Próbkowanie rozkładu średniej

Przez Benjamin Anderson 3 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, jaki jest rozkład średniej próby w statystyce. Znajdziesz tu także wzór na średni rozkład próbkowania i krok po kroku rozwiązane ćwiczenie.

Jaki jest rozkład średniej z próbkowania?

Rozkład średniej próbkowania (lub rozkład średnich próbkowania ) to rozkład wynikający z obliczenia średniej próbkowania każdej możliwej próbki z populacji. Oznacza to, że zbiór średnich próbek ze wszystkich możliwych próbek z populacji tworzy rozkład próbkowania średniej.

Innymi słowy, jeśli przeanalizujemy wszystkie próbki, które można pobrać z populacji i obliczymy średnią z każdej z próbek, zbiór obliczonych wartości tworzy rozkład próbkowania średniej próbki.

W statystyce rozkład średniej próby służy do obliczenia prawdopodobieństwa zbliżenia się do wartości średniej populacji podczas analizy pojedynczej próbki.

Wzór na rozkład średniej próby

Biorąc pod uwagę populację, która ma normalny rozkład prawdopodobieństwa ze średnią

$\mu$

i odchylenie standardowe

$\sigma$

i pobierane są próbki wielkości

$n$

, rozkład średniej próby będzie również określony rozkładem normalnym mającym następujące cechy:

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

Złoto

$\mu_{\overline{x}}$

jest średnią rozkładu próby średniej i

$\sigma_{\overline{x}}$

jest jego odchyleniem standardowym. Ponadto,

$\cfrac{\sigma}{\sqrt{n}}$

jest błędem standardowym rozkładu próbkowania.

Uwaga: Jeżeli populacja nie ma rozkładu normalnego, ale wielkość próby jest duża (n>30), rozkład średniej próby można również przybliżyć do poprzedniego rozkładu normalnego za pomocą centralnego twierdzenia granicznego.

Dlatego też, ponieważ rozkład średniej z próby ma rozkład normalny, wzór na obliczenie prawdopodobieństwa związanego ze średnią z próbki jest następujący:

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

Złoto:

$\overline{x}$

to przykładowe środki.
$\mu$

To jest średnia populacji.
$s$

jest odchyleniem standardowym populacji.
$n$

to wielkość próbki.
$Z$

jest zmienną zdefiniowaną przez standardowy rozkład normalny N(0,1).

Rzeczywisty przykład rozkładu średniej w próbce

Po zapoznaniu się z definicją rozkładu średniej z próbkowania i związanymi z nią wzorami, rozwiążmy przykład, aby lepiej zrozumieć tę koncepcję.

Waga studentów uniwersytetów ma rozkład normalny ze średnią 68 kg i odchyleniem standardowym 9 kg. Określony:
1. Jakie jest prawdopodobieństwo, że średnia w losowej próbie 25 uczniów będzie mniejsza niż 66 kg?
2. Jeśli zostanie pobranych 300 próbek po 25 uczniów każda, ile średnich próbek będzie miało wartość mniejszą niż 66 kg?

Przede wszystkim musimy obliczyć wartość odpowiedniej statystyki, w tym celu stosujemy wzór, który widzieliśmy powyżej:

$\displaystyle Z=\frac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}=\frac{66-68}{\displaystyle\frac{9}{\sqrt{25}}}=-1,11$

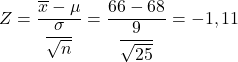
Prawdopodobieństwo, którego szukamy, jest zatem takie, które odpowiada wartości Z=-1,11 lewego ogona standardowego rozkładu normalnego, co można łatwo uzyskać z tabeli prawdopodobieństwa Z. Dlatego używamy tabeli Z, aby określić prawdopodobieństwo, że problem zadaje nam pytanie:

$P[\overline{x}\leq 66]=P[Z\leq -1,11] =0,1335$

➤ Patrz: Tabela Z

Teraz, gdy znamy prawdopodobieństwo, że średnia próbki losowej jest mniejsza niż 66 kg, aby wiedzieć, że liczba próbek oznacza mniej niż 66 kg, biorąc pod uwagę 300 równych próbek, musimy pomnożyć obliczone prawdopodobieństwo przez całkowitą liczbę pobranych próbek:

$0,1335\cdot 300 =40,05 \approx 40$

Dlatego też około 40 wyekstrahowanych próbek będzie miało średnią masę mniejszą niż 66 kg.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej

Jaki jest rozkład średniej z próbkowania?

Wzór na rozkład średniej próby

Rzeczywisty przykład rozkładu średniej w próbce

o autorze

Dr Benjamin Anderson

Dodaj komentarz