Jak utworzyć przedział ufności za pomocą rozkładu f
Aby ustalić, czy wariancje dwóch populacji są równe, możemy obliczyć współczynnik wariancji σ 2 1 / σ 2 2 , gdzie σ 2 1 jest wariancją populacji 1, a σ 2 2 jest wariancją populacji 2.
Aby oszacować prawdziwy współczynnik wariancji populacji, zazwyczaj bierzemy prostą próbkę losową z każdej populacji i obliczamy współczynnik wariancji próbki, s 1 2 / s 2 2 , gdzie s 1 2 i s 2 2 są wariancjami próbki dla próbki 1 i próbki . 2, odpowiednio.
W tym teście założono, że s 1 2 i s 2 2 oblicza się na podstawie niezależnych próbek o wielkości n 1 i n 2 , obie z populacji o rozkładzie normalnym.
Im dalej ten stosunek jest od jedności, tym silniejszy dowód na nierówne wariancje w obrębie populacji.
Przedział ufności (1-α)100% dla σ 2 1 / σ 2 2 definiuje się jako:
(s 1 2 / s 2 2 ) * F n 1 -1, n 2 -1, α/2 ≤ σ 2 1 / σ 2 2 ≤ (s 1 2 / s 2 2 ) * F n 2 -1, n 1-1 , α/2
gdzie F n 2 -1, n 1 -1, α/2 i F n 1 -1, n 2 -1, α/2 są wartościami krytycznymi rozkładu F dla wybranego poziomu istotności α.
Poniższe przykłady ilustrują, jak utworzyć przedział ufności dla σ 2 1 / σ 2 2 przy użyciu trzech różnych metod:
- Za rękę
- Skorzystaj z Microsoft Excela
- Korzystanie z oprogramowania statystycznego R
W każdym z poniższych przykładów wykorzystamy następujące informacje:
- α = 0,05
- n 1 = 16
- n2 = 11
- s 1 2 = 28,2
- s 2 2 = 19,3
Ręczne tworzenie przedziału ufności
Aby ręcznie obliczyć przedział ufności dla σ 2 1 / σ 2 2 , po prostu podstawiamy otrzymane liczby do wzoru na przedział ufności:
(s 1 2 / s 2 2 ) * F n1-1, n2-1,α/2 ≤ σ 2 1 / σ 2 2 ≤ (s 1 2 / s 2 2 ) * F n2-1, n1-1, α/2
Jedyne liczby, których nam brakuje, to wartości krytyczne. Na szczęście możemy zlokalizować te wartości krytyczne w tablicy rozkładu F :
F n2-1, n1-1, α/2 = F 10, 15, 0,025 = 3,0602
F n1-1, n2-1, α/2 = 1/ F 15, 10, 0,025 = 1 / 3,5217 = 0,2839
(Kliknij, aby powiększyć tabelę)
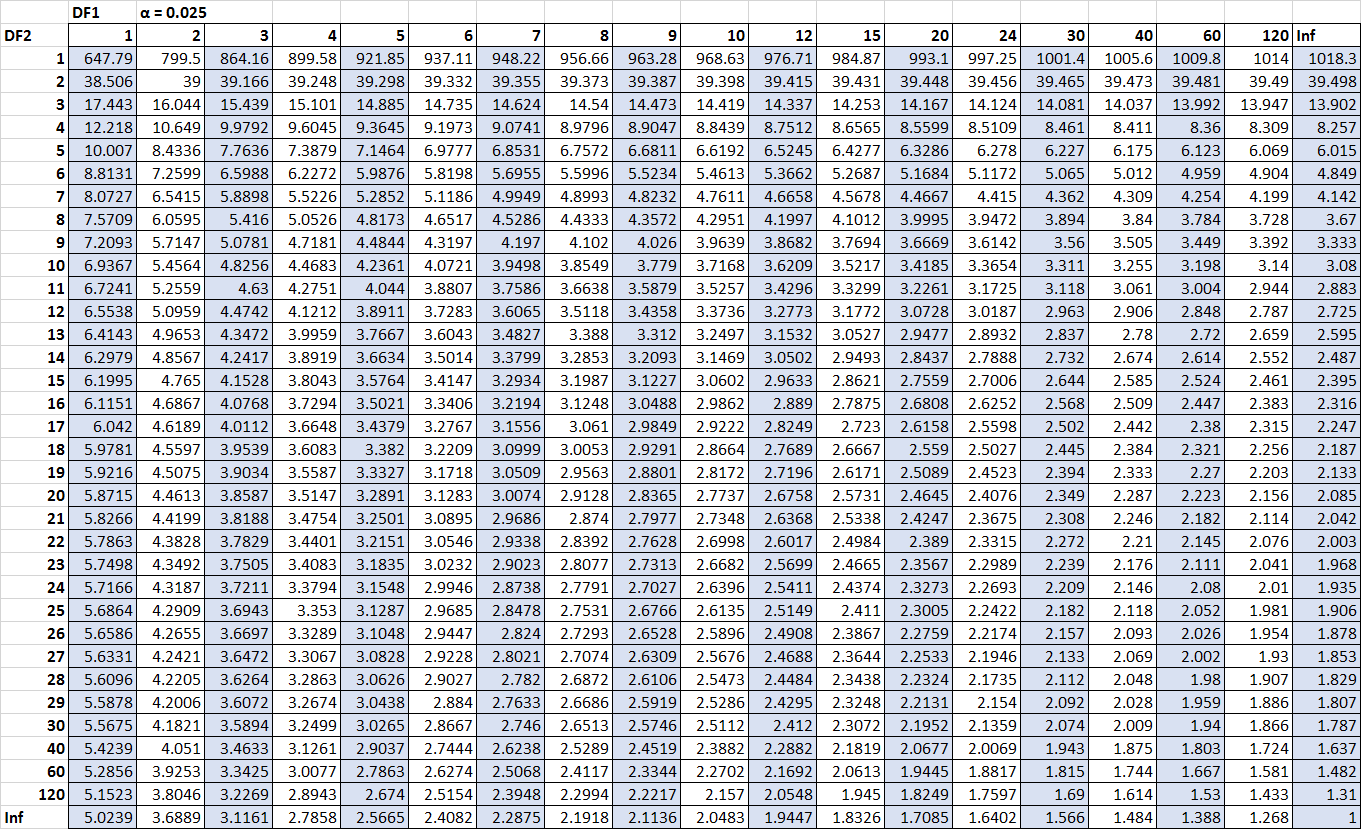
Możemy teraz podłączyć wszystkie liczby do przedziału wzoru ufności:
(s 1 2 / s 2 2 ) * F n1-1, n2-1,α/2 ≤ σ 2 1 / σ 2 2 ≤ (s 1 2 / s 2 2 ) * F n2-1, n1-1, α/2
(28,2 / 19,3) * (0,2839) ≤ σ 2 1 / σ 2 2 ≤ (28,2 / 19,3) * (3,0602)
0,4148 ≤ σ 2 1 / σ 2 2 ≤ 4,4714
Zatem 95% przedział ufności dla stosunku wariancji populacji wynosi (0,4148; 4,4714) .
Tworzenie przedziału ufności za pomocą programu Excel
Poniższy obraz pokazuje, jak obliczyć 95% przedział ufności dla współczynnika wariancji populacji w programie Excel. Dolne i górne granice przedziału ufności pokazano w kolumnie E, a wzór na znalezienie dolnej i górnej granicy pokazano w kolumnie F:
Zatem 95% przedział ufności dla stosunku wariancji populacji wynosi (0,4148; 4,4714) . Odpowiada to temu, co otrzymaliśmy, gdy ręcznie obliczyliśmy przedział ufności.
Tworzenie przedziału ufności za pomocą R
Poniższy kod ilustruje sposób obliczenia 95% przedziału ufności dla stosunku wariancji populacji w R:
#define significance level, sample sizes, and sample variances alpha <- .05 n1 <- 16 n2 <- 11 var1 <- 28.2 var2 <- 19.3 #define F critical values upper_crit <- 1/qf(alpha/2, n1-1, n2-1) lower_crit <- qf(alpha/2, n2-1, n1-1) #find confidence interval lower_bound <- (var1/var2) * lower_crit upper_bound <- (var1/var2) * upper_crit #output confidence interval paste0("(", lower_bound, ", ", upper_bound, " )") #[1] "(0.414899337980266, 4.47137571035219 )"
Zatem 95% przedział ufności dla stosunku wariancji populacji wynosi (0,4148; 4,4714) . Odpowiada to temu, co otrzymaliśmy, gdy ręcznie obliczyliśmy przedział ufności.
Dodatkowe zasoby
Jak czytać tablicę rozdzielczą F
Jak znaleźć wartość krytyczną F w Excelu