Wprowadzenie do rozkładu wielomianowego

Rozkład wielomianowy opisuje prawdopodobieństwo uzyskania określonej liczby zliczeń dla k różnych wyników, gdy każdy wynik ma stałe prawdopodobieństwo wystąpienia.

_{Jeśli zmienną} losową _{_} można znaleźć za pomocą następującego wzoru :

Prawdopodobieństwo = n! * (p ₁ ^{x ₁} * p ₂ ^{x ₂} * … * p _k ^{x _k} ) / (x ₁ ! * x ₂ ! … * x _k !)

Złoto:

• n: całkowita liczba zdarzeń
• x ₁ : liczba wystąpień wyniku 1
• p ₁ : prawdopodobieństwo, że w danej próbie wystąpi wynik 1

Załóżmy na przykład, że w urnie znajduje się 5 czerwonych kulek, 3 zielone kulki i 2 niebieskie kulki. Jeśli losowo wylosujemy z urny 5 kulek, jakie jest prawdopodobieństwo, że otrzymamy dokładnie 2 czerwone kulki, 2 zielone kulki i 1 niebieską kulkę?

Aby odpowiedzieć na to pytanie, możemy skorzystać z rozkładu wielomianowego z następującymi parametrami:

• n : 5
• x ₁ (# czerwonych kulek) = 2, x ₂ (# zielonych kulek) = 2, x ₃ (# niebieskich kulek) = 1
• p ₁ (prawdopodobny czerwony) = 0,5, p ₂ (prawdopodobny zielony) = 0,3, p ₃ (prawdopodobny niebieski) = 0,2

Podstawiając te liczby do wzoru, stwierdzamy, że prawdopodobieństwo wynosi:

Prawdopodobieństwo = 5! * (.5 ² * .3 ² * .2 ¹ ) / (2! * 2! * 1!) = 0,135 .

Problemy praktyki rozkładu wielomianowego

Skorzystaj z poniższych problemów praktycznych, aby sprawdzić swoją wiedzę na temat rozkładu wielomianowego.

Uwaga: Do obliczenia odpowiedzi na te pytania użyjemy kalkulatora rozkładu wielomianowego .

Problem 1

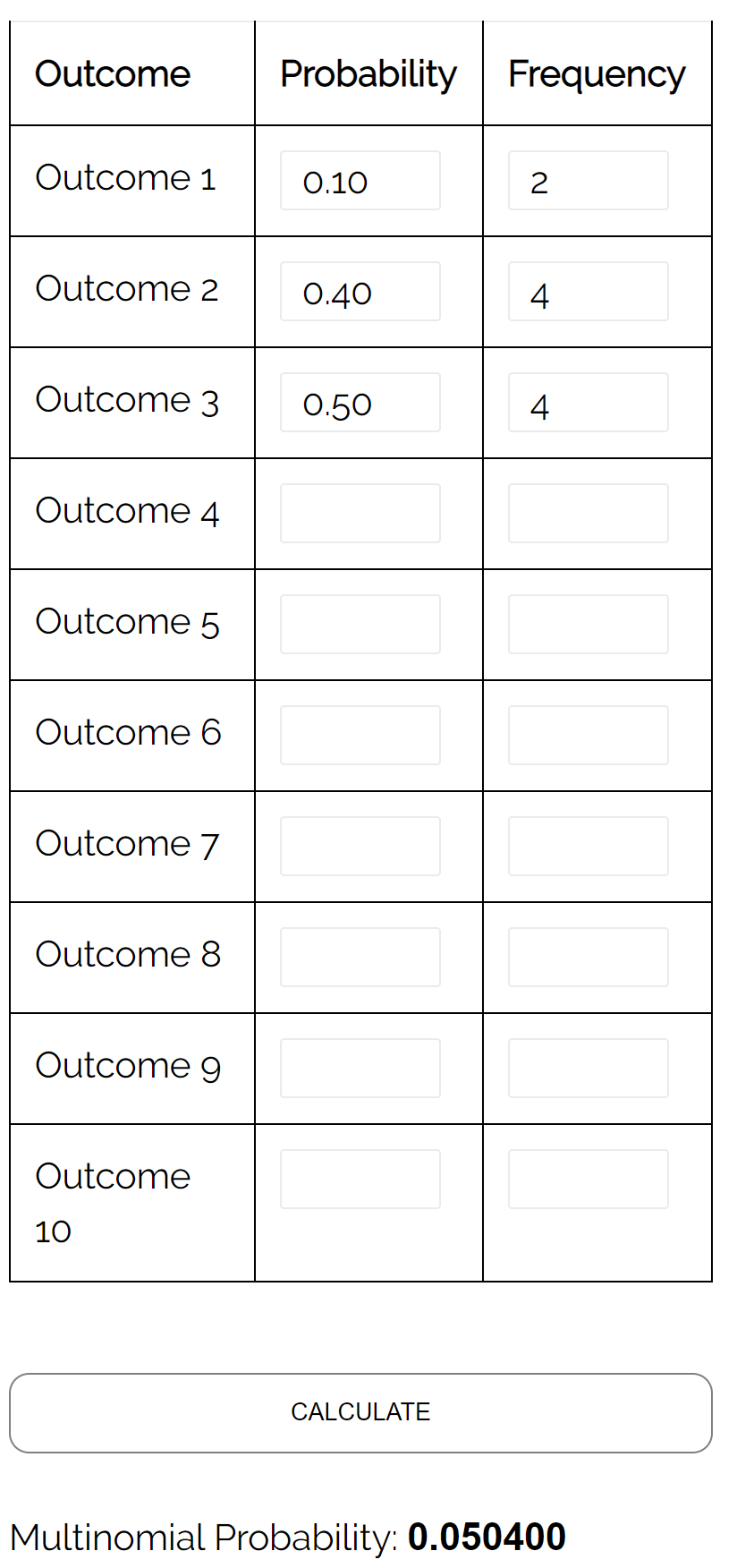
Pytanie: W trójstronnych wyborach na burmistrza kandydat A otrzymuje 10% głosów, kandydat B otrzymuje 40% głosów, a kandydat C otrzymuje 50% głosów. Jeśli wybierzemy losową próbę 10 wyborców, jakie jest prawdopodobieństwo, że 2 głosowało na kandydata A, 4 głosowało na kandydata B, a 4 głosowało na kandydata C?

Odpowiedź: Używając kalkulatora rozkładu wielomianowego z następującymi danymi wejściowymi, stwierdzamy, że prawdopodobieństwo wynosi 0,0504:

Problem 2

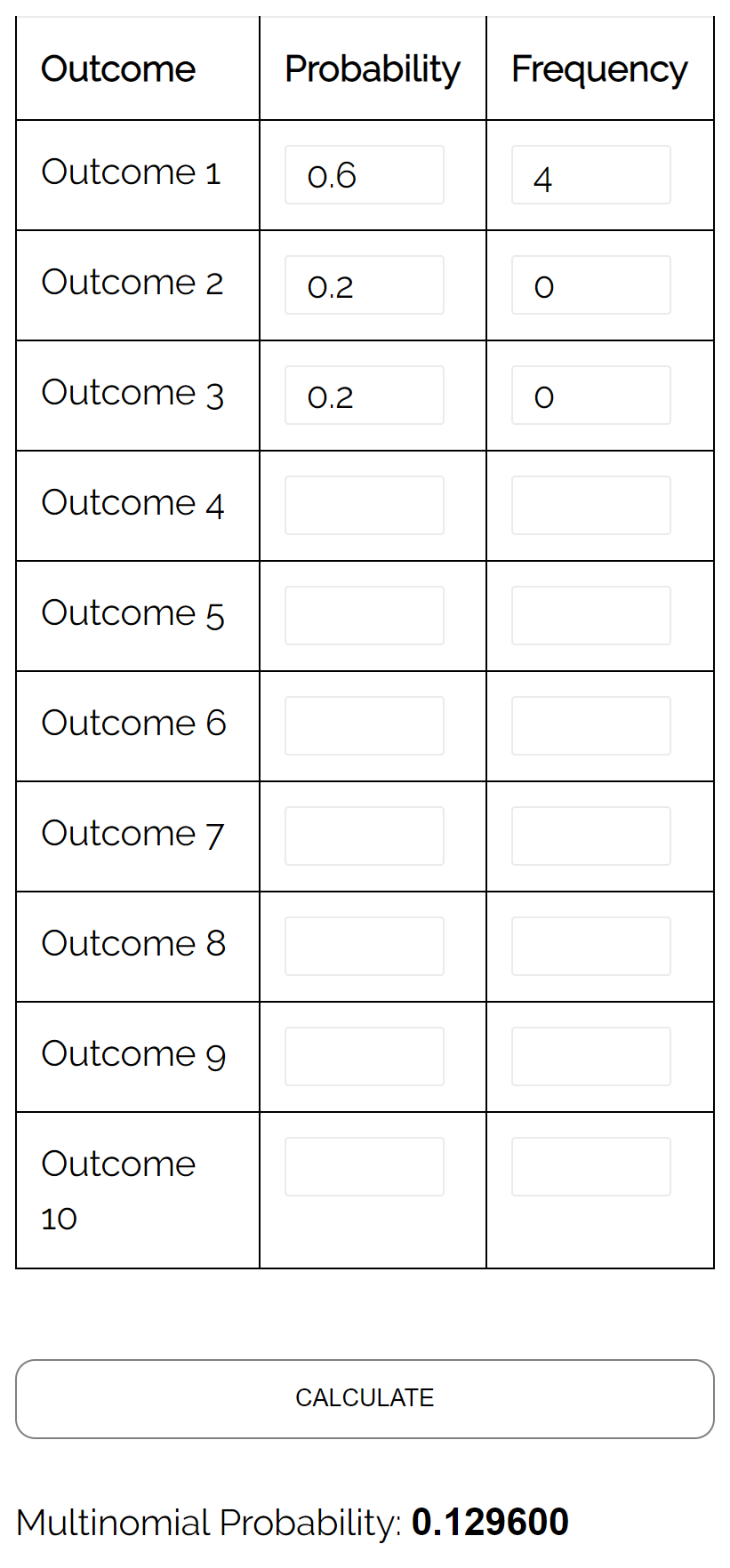
Pytanie: Załóżmy, że w urnie znajduje się 6 żółtych kulek, 2 czerwone kulki i 2 różowe kulki. Jeśli losowo wybierzemy z urny 4 kule, zastępując je, jakie jest prawdopodobieństwo, że wszystkie 4 kule będą żółte?

Odpowiedź: Używając kalkulatora rozkładu wielomianowego z następującymi danymi wejściowymi, stwierdzamy, że prawdopodobieństwo wynosi 0,1296:

Problem 3

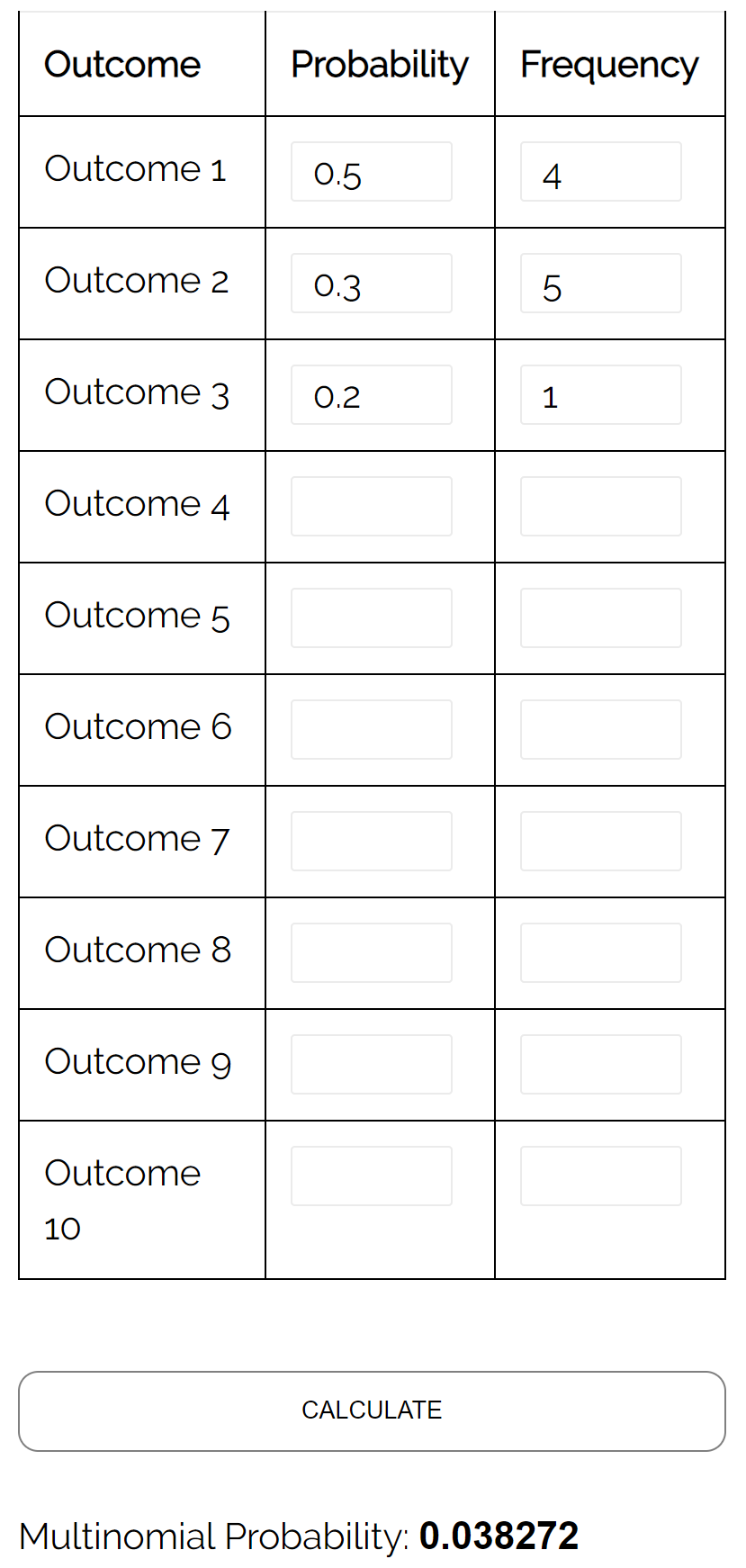
Pytanie: Załóżmy, że dwóch uczniów gra przeciwko sobie w szachy. Prawdopodobieństwo, że uczeń A wygra daną grę wynosi 0,5, prawdopodobieństwo, że uczeń B wygra daną grę wynosi 0,3, a prawdopodobieństwo, że w danej grze będzie remis wynosi 0, 2. Jeśli rozegrają 10 gier, jaki będzie wynik prawdopodobieństwo, że gracz A wygra 4 razy, gracz B 5 razy i że zremisuje 1 raz?

Odpowiedź: Używając kalkulatora rozkładu wielomianowego z następującymi danymi wejściowymi, stwierdzamy, że prawdopodobieństwo wynosi 0,038272:

Dodatkowe zasoby

Poniższe samouczki stanowią wprowadzenie do innych popularnych rozkładów w statystykach:

Wprowadzenie do rozkładu normalnego
Wprowadzenie do rozkładu dwumianowego
Wprowadzenie do rozkładu Poissona
Wprowadzenie do rozkładu geometrycznego